Standard translation
Jump to navigation
Jump to search
Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.
Basic definition
- left R-module
- A left module over the ring is an abelian group with an operation (called scalar multipliction) satisfies the following condition:
- right R-module
- A right module over the ring is an abelian group with an operation satisfies the following condition:
- Or it can be defined as the left module over (the opposite ring of ).
- bimodule
- If an abelian group is both a left -module and right -module, it can be made to a -bimodule if .
- submodule
- Given is a left -module, a subgroup of is a submodule if .
- homomorphism of -modules
- For two left -modules , a group homomorphism is called homomorphism of -modules if .
- quotient module
- Given a left -modules , a submodule , can be made to a left -module by . It is also called a factor module.
- annihilator
- The annihilator of a left -module is the set . It is a (left) ideal of .
- The annihilator of an element is the set .
Types of modules
- finitely generated module
- A module is finitely generated if there exist finitely many elements in such that every element of is a finite linear combination of those elements with coefficients from the scalar ring .
- cyclic module
- A module is called a cyclic module if it is generated by one element.
- free module
- A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring .
- Projective module
- A -module is called a projective module if given a -module homomorphism , and a surjective -module homomorphism , there exists a -module homomorphism such that .
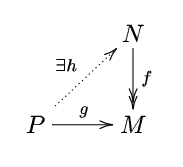
- The following conditions are equivalent:
- The covariant functor is exact.
- is a projective module.
- Every short exact sequence is split.
- is a direct summand of free modules.
- In particular, every free module is projective.
- injective module
- A -module is called an injective module if given a -module homomorphism , and an injective -module homomorphism , there exists a
-module homomorphism such that .

- The following conditions are equivalent:
- The contravariant functor is exact.
- is a injective module.
- Every short exact sequence is split.
- flat module
- A -module is called a flat module if the tensor product functor is exact.
- In particular, every projective module is flat.
- simple module
- A simple module is a nonzero module whose only submodules are zero and itself.
- indecomposable module
- An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable.
- principal indecomposable module
- A cyclic indecomposable projective module is known as a PIM.
- semisimple module
- A module is called semisimple if it is the direct sum of simple submodules.
- faithful module
- A faithful module is one where the action of each nonzero on is nontrivial (i.e. for some x in M). Equivalently, is the zero ideal.
- Noetherian module
- A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.
- Artinian module
- An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.
- finite length module
- A module which is both Artinian and Noetherian has additional special properties.
- graded module
- A module over a graded ring is a graded module if can be expressed as a direct sum and .
- invertible module
- Roughly synonymous to rank 1 projective module.
- uniform module
- Module in which every two non-zero submodules have a non-zero intersection.
- algebraically compact module (pure injective module)
- Modules in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.
- injective cogenerator
- An injective module such that every module has a nonzero homomorphism into it.
- irreducible module
- synonymous to "simple module"
- completely reducible module
- synonymous to "semisimple module"
Operations on modules
- Essential extension
- An extension in which every nonzero submodule of the larger module meets the smaller module in a nonzero submodule.
- Injective envelope
- A maximal essential extension, or a minimal embedding in an injective module
- Projective cover
- A minimal surjection from a projective module.
- Socle
- The largest semisimple submodule
- Radical of a module
- The intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.
Changing scalars
- Restriction of scalars
- Uses a ring homomorphism from R to S to convert S-modules to R-modules
- Extension of scalars
- Uses a ring homomorphism from R to S to convert R-modules to S-modules
- Localization of a module
- Converts R modules to S modules, where S is a localization of R
- Endomorphism ring
- A left R-module is a right S-module where S is its endomorphism ring.
Homological algebra
Modules over special rings
- D-module
- A module over a ring of differential operators.
- Drinfeld module
- A module over a ring of functions on algebraic curve with coefficients from a finite field.
- Galois module
- A module over the group ring of a Galois group
- Structure theorem for finitely generated modules over a principal ideal domain
- Finitely generated modules over PIDs are finite direct sums of primary cyclic modules.
- Tate module
- A special kind of Galois module
Miscellaneous
- Rational canonical form
- elementary divisor
- invariants
- fitting ideal
- normal forms for matrices
- Jordan Hölder composition series
- tensor product
See also
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010