Incompressible surface
Name: Jodi Junker
My age: 32
Country: Netherlands
Home town: Oudkarspel
Post code: 1724 Xg
Street: Waterlelie 22
my page - www.hostgator1centcoupon.info
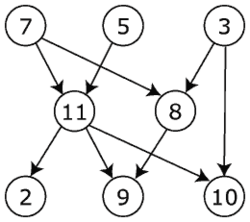
In computer science, a topological sort (sometimes abbreviated topsort or toposort) or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.
Examples
The canonical application of topological sorting (topological order) is in scheduling a sequence of jobs or tasks based on their dependencies; topological sorting algorithms were first studied in the early 1960s in the context of the PERT technique for scheduling in project management Template:Harv. The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes to dry). Then, a topological sort gives an order in which to perform the jobs.
In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in makefiles, data serialization, and resolving symbol dependencies in linkers. It is also used to decide in which order to load tables with foreign keys in databases.
Algorithms
The usual algorithms for topological sorting have running time linear in the number of nodes plus the number of edges ().
One of these algorithms, first described by Template:Harvtxt, works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" which have no incoming edges and insert them into a set S; at least one such node must exist in an acyclic graph. Then:
L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
add n to tail of L
for each node m with an edge e from n to m do
remove edge e from the graph
if m has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least one cycle)
else
return L (a topologically sorted order)
If the graph is a DAG, a solution will be contained in the list L (the solution is not necessarily unique). Otherwise, the graph must have at least one cycle and therefore a topological sorting is impossible.
Reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created. A variation of Kahn's algorithm that breaks ties lexicographically forms a key component of the Coffman–Graham algorithm for parallel scheduling and layered graph drawing.
An alternative algorithm for topological sorting is based on depth-first search. The algorithm loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort:
L ← Empty list that will contain the sorted nodes
while there are unmarked nodes do
select an unmarked node n
visit(n)
function visit(node n)
if n has a temporary mark then stop (not a DAG)
if n is not marked (i.e. has not been visited yet) then
mark n temporarily
for each node m with an edge from n to m do
visit(m)
mark n permanently
add n to head of L
Each node n gets prepended to the output list L only after considering all other nodes on which n depends (all ancestral nodes of n in the graph). Specifically, when the algorithm adds node n, we are guaranteed that all nodes on which n depends are already in the output list L: they were added to L either by the preceding recursive call to visit(), or by an earlier call to visit(). Since each edge and node is visited once, the algorithm runs in linear time. This depth-first-search-based algorithm is the one described by Template:Harvtxt; it seems to have been first described in print by Template:Harvtxt.
Complexity
The computational complexity of the problem of computing a topological ordering of a directed acyclic graph is NC2; that is, it can be computed in O(log2 n) time on a parallel computer using a polynomial number O(nk) of processors, for some constant k Template:Harv. One method for doing this is to repeatedly square the adjacency matrix of the given graph, logarithmically many times, using min-plus matrix multiplication with maximization in place of minimization. The resulting matrix describes the longest path distances in the graph. Sorting the vertices by the lengths of their longest incoming paths produces a topological ordering Template:Harv.
Uniqueness
If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian path in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in linear time whether a unique ordering exists, and whether a Hamiltonian path exists, despite the NP-hardness of the Hamiltonian path problem for more general directed graphs Template:Harv.
Relation to partial orders
Topological orderings are also closely related to the concept of a linear extension of a partial order in mathematics.
A partially ordered set is just a set of objects together with a definition of the "≤" inequality relation, satisfying the axioms of reflexivity (x ≤ x), antisymmetry (if x ≤ y and y ≤x then x = y) and transitivity (if x ≤ y and y ≤ z, then x ≤ z). A total order is a partial order in which, for every two objects x and y in the set, either x ≤ y or y ≤ x. Total orders are familiar in computer science as the comparison operators needed to perform comparison sorting algorithms. For finite sets, total orders may be identified with linear sequences of objects, where the "≤" relation is true whenever the first object precedes the second object in the order; a comparison sorting algorithm may be used to convert a total order into a sequence in this way. A linear extension of a partial order is a total order that is compatible with it, in the sense that, if x ≤ y in the partial order, then x ≤ y in the total order as well.
One can define a partial ordering from any DAG by letting the set of objects be the vertices of the DAG, and defining x ≤ y to be true, for any two vertices x and y, whenever there exists a directed path from x to y; that is, whenever y is reachable from x. With these definitions, a topological ordering of the DAG is the same thing as a linear extension of this partial order. Conversely, any partial ordering may be defined as the reachability relation in a DAG. One way of doing this is to define a DAG that has a vertex for every object in the partially ordered set, and an edge xy for every pair of objects for which x ≤ y. An alternative way of doing this is to use the transitive reduction of the partial ordering; in general, this produces DAGs with fewer edges, but the reachability relation in these DAGs is still the same partial order. By using these constructions, one can use topological ordering algorithms to find linear extensions of partial orders.
See also
- tsort, a Unix program for topological sorting
- dep-trace Orders basic dependencies and unfolds nested ones. (basic: without 2D graphical presumption)
- Feedback arc set, a (possibly empty) set of arcs which, if removed from the graph, make it possible to topologically sort it. Useful for dealing with graphs with cycles.
- D. E. Knuth, The Art of Computer Programming, Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history.
- Dependency graph
References
- Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010.
External links
- NIST Dictionary of Algorithms and Data Structures: topological sort
I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog.