Field equation
Diving Coach (Open water ) Dominic from Kindersley, loves to spend some time classic cars, property developers in singapore house for rent (Source Webpage) and greeting card collecting. Finds the world an interesting place having spent 8 days at Cidade Velha.
General relativity is a theory of gravitation that was developed by Albert Einstein between 1907 and 1915. According to general relativity, the observed gravitational effect between masses results from their warping of spacetime.
By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force,[1] the basic framework was extremely successful at describing motion.
Experiments and observations show that Einstein's description of gravitation accounts for several effects that are unexplained by Newton's law, such as minute anomalies in the orbits of Mercury and other planets. General relativity also predicts novel effects of gravity, such as gravitational waves, gravitational lensing and an effect of gravity on time known as gravitational time dilation. Many of these predictions have been confirmed by experiment, while others are the subject of ongoing research. For example, although there is indirect evidence for gravitational waves, direct evidence of their existence is still being sought by several teams of scientists in experiments such as the LIGO and GEO 600 projects.
General relativity has developed into an essential tool in modern astrophysics. It provides the foundation for the current understanding of black holes, regions of space where the gravitational effect is so strong that not even light can escape. Their strong gravity is thought to be responsible for the intense radiation emitted by certain types of astronomical objects (such as active galactic nuclei or microquasars). General relativity is also part of the framework of the standard Big Bang model of cosmology.
Although general relativity is not the only relativistic theory of gravity, it is the simplest such theory that is consistent with the experimental data. Nevertheless, a number of open questions remain, the most fundamental of which is how general relativity can be reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.
From special to general relativity
In September 1905, Albert Einstein published his theory of special relativity, which reconciles Newton's laws of motion with electrodynamics (the interaction between objects with electric charge). Special relativity introduced a new framework for all of physics by proposing new concepts of space and time. Some then-accepted physical theories were inconsistent with that framework; a key example was Newton's theory of gravity, which describes the mutual attraction experienced by bodies due to their mass.
Several physicists, including Einstein, searched for a theory that would reconcile Newton's law of gravity and special relativity. Only Einstein's theory proved to be consistent with experiments and observations. To understand the theory's basic ideas, it is instructive to follow Einstein's thinking between 1907 and 1915, from his simple thought experiment involving an observer in free fall to his fully geometric theory of gravity.[2]
Equivalence principle
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. A person in a free-falling elevator experiences weightlessness, and objects either float motionless or drift at constant speed. Since everything in the elevator is falling together, no gravitational effect can be observed. In this way, the experiences of an observer in free fall are indistinguishable from those of an observer in deep space, far from any significant source of gravity. Such observers are the privileged ("inertial") observers Einstein described in his theory of special relativity: observers for whom light travels along straight lines at constant speed.[3]
Einstein hypothesized that the similar experiences of weightless observers and inertial observers in special relativity represented a fundamental property of gravity, and he made this the cornerstone of his theory of general relativity, formalized in his equivalence principle. Roughly speaking, the principle states that a person in a free-falling elevator cannot tell that they are in free fall. Every experiment in such a free-falling environment has the same results as it would for an observer at rest or moving uniformly in deep space, far from all sources of gravity.[4]
Gravity and acceleration
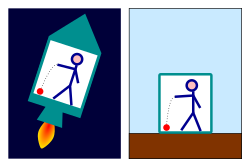
Most effects of gravity vanish in free fall, but effects that seem the same as those of gravity can be produced by an accelerated frame of reference. An observer in a closed room cannot tell which of the following is true:
- Objects are falling to the floor because the room is resting on the surface of the Earth and the objects are being pulled down by gravity.
- Objects are falling to the floor because the room is aboard a rocket in space, which is accelerating at 9.81 m/s2 and is far from any source of gravity. The objects are being pulled towards the floor by the same "inertial force" that presses the driver of an accelerating car into the back of his seat.
Conversely, any effect observed in an accelerated reference frame should also be observed in a gravitational field of corresponding strength. This principle allowed Einstein to predict several novel effects of gravity in 1907, as explained in the next section.
An observer in an accelerated reference frame must introduce what physicists call fictitious forces to account for the acceleration experienced by himself and objects around him. One example, the force pressing the driver of an accelerating car into his or her seat, has already been mentioned; another is the force you can feel pulling your arms up and out if you attempt to spin around like a top. Einstein's master insight was that the constant, familiar pull of the Earth's gravitational field is fundamentally the same as these fictitious forces.[5] The apparent magnitude of the fictitious forces always appears to be proportional to the mass of any object on which they act - for instance, the driver's seat exerts just enough force to accelerate the driver at the same rate as the car. By analogy, Einstein proposed that an object in a gravitational field should feel a gravitational force proportional to its mass, as embodied in Newton's law of gravitation.[6]
Physical consequences
In 1907, Einstein was still eight years away from completing the general theory of relativity. Nonetheless, he was able to make a number of novel, testable predictions that were based on his starting point for developing his new theory: the equivalence principle.[7]

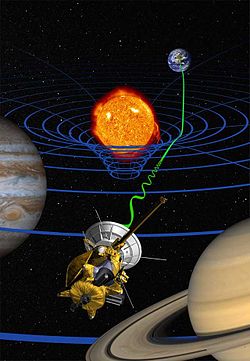
The first new effect is the gravitational frequency shift of light. Consider two observers aboard an accelerating rocket-ship. Aboard such a ship, there is a natural concept of "up" and "down": the direction in which the ship accelerates is "up", and unattached objects accelerate in the opposite direction, falling "downward". Assume that one of the observers is "higher up" than the other. When the lower observer sends a light signal to the higher observer, the acceleration causes the light to be red-shifted, as may be calculated from special relativity; the second observer will measure a lower frequency for the light than the first. Conversely, light sent from the higher observer to the lower is blue-shifted, that is, shifted towards higher frequencies.[8] Einstein argued that such frequency shifts must also be observed in a gravitational field. This is illustrated in the figure at left, which shows a light wave that is gradually red-shifted as it works its way upwards against the gravitational acceleration. This effect has been confirmed experimentally, as described below.
This gravitational frequency shift corresponds to a gravitational time dilation: Since the "higher" observer measures the same light wave to have a lower frequency than the "lower" observer, time must be passing faster for the higher observer. Thus, time runs more slowly for observers who are lower in a gravitational field.
It is important to stress that, for each observer, there are no observable changes of the flow of time for events or processes that are at rest in his or her reference frame. Five-minute-eggs as timed by each observer's clock have the same consistency; as one year passes on each clock, each observer ages by that amount; each clock, in short, is in perfect agreement with all processes happening in its immediate vicinity. It is only when the clocks are compared between separate observers that one can notice that time runs more slowly for the lower observer than for the higher.[9] This effect is minute, but it too has been confirmed experimentally in multiple experiments, as described below.
In a similar way, Einstein predicted the gravitational deflection of light: in a gravitational field, light is deflected downward. Quantitatively, his results were off by a factor of two; the correct derivation requires a more complete formulation of the theory of general relativity, not just the equivalence principle.[10]
Tidal effects

The equivalence between gravitational and inertial effects does not constitute a complete theory of gravity. When it comes to explaining gravity near our own location on the Earth's surface, noting that our reference frame is not in free fall, so that fictitious forces are to be expected, provides a suitable explanation. But a freely falling reference frame on one side of the Earth cannot explain why the people on the opposite side of the Earth experience a gravitational pull in the opposite direction.
A more basic manifestation of the same effect involves two bodies that are falling side by side towards the Earth. In a reference frame that is in free fall alongside these bodies, they appear to hover weightlessly – but not exactly so. These bodies are not falling in precisely the same direction, but towards a single point in space: namely, the Earth's center of gravity. Consequently, there is a component of each body's motion towards the other (see the figure). In a small environment such as a freely falling lift, this relative acceleration is minuscule, while for skydivers on opposite sides of the Earth, the effect is large. Such differences in force are also responsible for the tides in the Earth's oceans, so the term "tidal effect" is used for this phenomenon.
The equivalence between inertia and gravity cannot explain tidal effects – it cannot explain variations in the gravitational field.[11] For that, a theory is needed which describes the way that matter (such as the large mass of the Earth) affects the inertial environment around it.
From acceleration to geometry
In exploring the equivalence of gravity and acceleration as well as the role of tidal forces, Einstein discovered several analogies with the geometry of surfaces. An example is the transition from an inertial reference frame (in which free particles coast along straight paths at constant speeds) to a rotating reference frame (in which extra terms corresponding to fictitious forces have to be introduced in order to explain particle motion): this is analogous to the transition from a Cartesian coordinate system (in which the coordinate lines are straight lines) to a curved coordinate system (where coordinate lines need not be straight).
A deeper analogy relates tidal forces with a property of surfaces called curvature. For gravitational fields, the absence or presence of tidal forces determines whether or not the influence of gravity can be eliminated by choosing a freely falling reference frame. Similarly, the absence or presence of curvature determines whether or not a surface is equivalent to a plane. In the summer of 1912, inspired by these analogies, Einstein searched for a geometric formulation of gravity.[12]
The elementary objects of geometry – points, lines, triangles – are traditionally defined in three-dimensional space or on two-dimensional surfaces. In 1907, the mathematician Hermann Minkowski (who was Einstein's former mathematics professor in Swiss Federal Polytechnic) introduced a geometric formulation of Einstein's special theory of relativity in which the geometry included not only space, but also time. The basic entity of this new geometry is four-dimensional spacetime. The orbits of moving bodies are curves in spacetime; the orbits of bodies moving at constant speed without changing direction correspond to straight lines.[13]
For surfaces, the generalization from the geometry of a plane – a flat surface – to that of a general curved surface had been described in the early 19th century by Carl Friedrich Gauss. This description had in turn been generalized to higher-dimensional spaces in a mathematical formalism introduced by Bernhard Riemann in the 1850s. With the help of Riemannian geometry, Einstein formulated a geometric description of gravity in which Minkowski's spacetime is replaced by distorted, curved spacetime, just as curved surfaces are a generalization of ordinary plane surfaces.[14]
After he had realized the validity of this geometric analogy, it took Einstein a further three years to find the missing cornerstone of his theory: the equations describing how matter influences spacetime's curvature. Having formulated what are now known as Einstein's equations (or, more precisely, his field equations of gravity), he presented his new theory of gravity at several sessions of the Prussian Academy of Sciences in late 1915.[15]
Geometry and gravitation
Paraphrasing John Wheeler, Einstein's geometric theory of gravity can be summarized thus: spacetime tells matter how to move; matter tells spacetime how to curve.[16] What this means is addressed in the following three sections, which explore the motion of so-called test particles, examine which properties of matter serve as a source for gravity, and, finally, introduce Einstein's equations, which relate these matter properties to the curvature of spacetime.
Probing the gravitational field
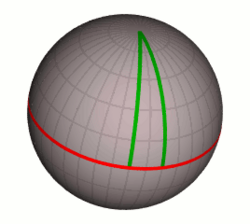
In order to map a body's gravitational influence, it is useful to think about what physicists call probe or test particles: particles that are influenced by gravity, but are so small and light that we can neglect their own gravitational effect. In the absence of gravity and other external forces, a test particle moves along a straight line at a constant speed. In the language of spacetime, this is equivalent to saying that such test particles move along straight world lines in spacetime. In the presence of gravity, spacetime is non-Euclidean, or curved, and in curved spacetime straight world lines may not exist. Instead, test particles move along lines called geodesics, which are "as straight as possible," that is, they follow the shortest path between starting and ending points, taking the curvature into consideration.
A simple analogy is the following: In geodesy, the science of measuring Earth's size and shape, a geodesic (from Greek "geo", Earth, and "daiein", to divide) is the shortest route between two points on the Earth's surface. Approximately, such a route is a segment of a great circle, such as a line of longitude or the equator. These paths are certainly not straight, simply because they must follow the curvature of the Earth's surface. But they are as straight as is possible subject to this constraint.
The properties of geodesics differ from those of straight lines. For example, on a plane, parallel lines never meet, but this is not so for geodesics on the surface of the Earth: for example, lines of longitude are parallel at the equator, but intersect at the poles. Analogously, the world lines of test particles in free fall are spacetime geodesics, the straightest possible lines in spacetime. But still there are crucial differences between them and the truly straight lines that can be traced out in the gravity-free spacetime of special relativity. In special relativity, parallel geodesics remain parallel. In a gravitational field with tidal effects, this will not, in general, be the case. If, for example, two bodies are initially at rest relative to each other, but are then dropped in the Earth's gravitational field, they will move towards each other as they fall towards the Earth's center.[17]
Compared with planets and other astronomical bodies, the objects of everyday life (people, cars, houses, even mountains) have little mass. Where such objects are concerned, the laws governing the behavior of test particles are sufficient to describe what happens. Notably, in order to deflect a test particle from its geodesic path, an external force must be applied. A person sitting on a chair is trying to follow a geodesic, that is, to fall freely towards the center of the Earth. But the chair applies an external upwards force preventing the person from falling. In this way, general relativity explains the daily experience of gravity on the surface of the Earth not as the downwards pull of a gravitational force, but as the upwards push of external forces. These forces deflect all bodies resting on the Earth's surface from the geodesics they would otherwise follow.[18] For matter objects whose own gravitational influence cannot be neglected, the laws of motion are somewhat more complicated than for test particles, although it remains true that spacetime tells matter how to move.[19]
Sources of gravity
In Newton's description of gravity, the gravitational force is caused by matter. More precisely, it is caused by a specific property of material objects: their mass. In Einstein's theory and related theories of gravitation, curvature at every point in spacetime is also caused by whatever matter is present. Here, too, mass is a key property in determining the gravitational influence of matter. But in a relativistic theory of gravity, mass cannot be the only source of gravity. Relativity links mass with energy, and energy with momentum.
The equivalence between mass and energy, as expressed by the formula E = mc2, is the most famous consequence of special relativity. In relativity, mass and energy are two different ways of describing one physical quantity. If a physical system has energy, it also has the corresponding mass, and vice versa. In particular, all properties of a body that are associated with energy, such as its temperature or the binding energy of systems such as nuclei or molecules, contribute to that body's mass, and hence act as sources of gravity.[20]
In special relativity, energy is closely connected to momentum. Just as space and time are, in that theory, different aspects of a more comprehensive entity called spacetime, energy and momentum are merely different aspects of a unified, four-dimensional quantity that physicists call four-momentum. In consequence, if energy is a source of gravity, momentum must be a source as well. The same is true for quantities that are directly related to energy and momentum, namely internal pressure and tension. Taken together, in general relativity it is mass, energy, momentum, pressure and tension that serve as sources of gravity: they are how matter tells spacetime how to curve. In the theory's mathematical formulation, all these quantities are but aspects of a more general physical quantity called the energy–momentum tensor.[21]
Einstein's equations
Einstein's equations are the centerpiece of general relativity. They provide a precise formulation of the relationship between spacetime geometry and the properties of matter, using the language of mathematics. More concretely, they are formulated using the concepts of Riemannian geometry, in which the geometric properties of a space (or a spacetime) are described by a quantity called a metric. The metric encodes the information needed to compute the fundamental geometric notions of distance and angle in a curved space (or spacetime).

A spherical surface like that of the Earth provides a simple example. The location of any point on the surface can be described by two coordinates: the geographic latitude and longitude. Unlike the Cartesian coordinates of the plane, coordinate differences are not the same as distances on the surface, as shown in the diagram on the right: for someone at the equator, moving 30 degrees of longitude westward (magenta line) corresponds to a distance of roughly Template:Convert. On the other hand, someone at a latitude of 55 degrees, moving 30 degrees of longitude westward (blue line) covers a distance of merely Template:Convert. Coordinates therefore do not provide enough information to describe the geometry of a spherical surface, or indeed the geometry of any more complicated space or spacetime. That information is precisely what is encoded in the metric, which is a function defined at each point of the surface (or space, or spacetime) and relates coordinate differences to differences in distance. All other quantities that are of interest in geometry, such as the length of any given curve, or the angle at which two curves meet, can be computed from this metric function.[22]
The metric function and its rate of change from point to point can be used to define a geometrical quantity called the Riemann curvature tensor, which describes exactly how the space (or spacetime) is curved at each point. In general relativity, the metric and the Riemann curvature tensor are quantities defined at each point in spacetime. As has already been mentioned, the matter content of the spacetime defines another quantity, the energy–momentum tensor T, and the principle that "spacetime tells matter how to move, and matter tells spacetime how to curve" means that these quantities must be related to each other. Einstein formulated this relation by using the Riemann curvature tensor and the metric to define another geometrical quantity G, now called the Einstein tensor, which describes some aspects of the way spacetime is curved. Einstein's equation then states that
i.e., up to a constant multiple, the quantity G (which measures curvature) is equated with the quantity T (which measures matter content). The constants involved in this equation reflect the different theories that went into its making: π is one of the basic constants of geometry, G is the gravitational constant that is already present in Newtonian gravity, and c is the speed of light, the key constant in special relativity.
This equation is often referred to in the plural as Einstein's equations, since the quantities G and T are each determined by several functions of the coordinates of spacetime, and the equations equate each of these component functions.[23] A solution of these equations describes a particular geometry of spacetime; for example, the Schwarzschild solution describes the geometry around a spherical, non-rotating mass such as a star or a black hole, whereas the Kerr solution describes a rotating black hole. Still other solutions can describe a gravitational wave or, in the case of the Friedmann–Lemaître–Robertson–Walker solution, an expanding universe. The simplest solution is the uncurved Minkowski spacetime, the spacetime described by special relativity.[24]
Experiments
No scientific theory is apodictically true; each is a model that must be checked by experiment. Newton's law of gravity was accepted because it accounted for the motion of planets and moons in the solar system with considerable accuracy. As the precision of experimental measurements gradually improved, some discrepancies with Newton's predictions were observed, and these were accounted for in the general theory of relativity. Similarly, the predictions of general relativity must also be checked with experiment, and Einstein himself devised three tests now known as the classical tests of the theory:
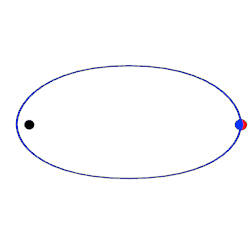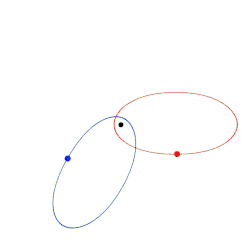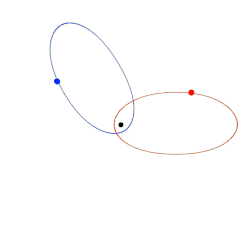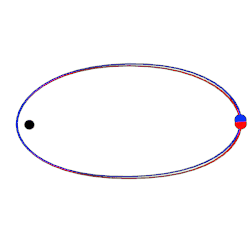
- Newtonian gravity predicts that the orbit which a single planet traces around a perfectly spherical star should be an ellipse. Einstein's theory predicts a more complicated curve: the planet behaves as if it were travelling around an ellipse, but at the same time, the ellipse as a whole is rotating slowly around the star. In the diagram on the right, the ellipse predicted by Newtonian gravity is shown in red, and part of the orbit predicted by Einstein in blue. For a planet orbiting the Sun, this deviation from Newton's orbits is known as the anomalous perihelion shift. The first measurement of this effect, for the planet Mercury, dates back to 1859. The most accurate results for Mercury and for other planets to date are based on measurements which were undertaken between 1966 and 1990, using radio telescopes.[25] General relativity predicts the correct anomalous perihelion shift for all planets where this can be measured accurately (Mercury, Venus and the Earth).
- According to general relativity, light does not travel along straight lines when it propagates in a gravitational field. Instead, it is deflected in the presence of massive bodies. In particular, starlight is deflected as it passes near the Sun, leading to apparent shifts of up 1.75 arc seconds in the stars' positions in the sky (an arc second is equal to 1/3600 of a degree). In the framework of Newtonian gravity, a heuristic argument can be made that leads to light deflection by half that amount. The different predictions can be tested by observing stars that are close to the Sun during a solar eclipse. In this way, a British expedition to West Africa in 1919, directed by Arthur Eddington, confirmed that Einstein's prediction was correct, and the Newtonian predictions wrong, via observation of the May 1919 eclipse. Eddington's results were not very accurate; subsequent observations of the deflection of the light of distant quasars by the Sun, which utilize highly accurate techniques of radio astronomy, have confirmed Eddington's results with significantly better precision (the first such measurements date from 1967, the most recent comprehensive analysis from 2004).[26]
- Gravitational redshift was first measured in a laboratory setting in 1959 by Pound and Rebka. It is also seen in astrophysical measurements, notably for light escaping the white dwarf Sirius B. The related gravitational time dilation effect has been measured by transporting atomic clocks to altitudes of between tens and tens of thousands of kilometers (first by Hafele and Keating in 1971; most accurately to date by Gravity Probe A launched in 1976).[27]
Of these tests, only the perihelion advance of Mercury was known prior to Einstein's final publication of general relativity in 1916. The subsequent experimental confirmation of his other predictions, especially the first measurements of the deflection of light by the sun in 1919, catapulted Einstein to international stardom.[28] These three experiments justified adopting general relativity over Newton's theory and, incidentally, over a number of alternatives to general relativity that had been proposed.
Further tests of general relativity include precision measurements of the Shapiro effect or gravitational time delay for light, most recently in 2002 by the Cassini space probe. One set of tests focuses on effects predicted by general relativity for the behavior of gyroscopes travelling through space. One of these effects, geodetic precession, has been tested with the Lunar Laser Ranging Experiment (high-precision measurements of the orbit of the Moon). Another, which is related to rotating masses, is called frame-dragging. The geodetic and frame-dragging effects were both tested by the Gravity Probe B satellite experiment launched in 2004, with results confirming relativity to within 0.5% and 15%, respectively, as of December 2008.[29]
By cosmic standards, gravity throughout the solar system is weak. Since the differences between the predictions of Einstein's and Newton's theories are most pronounced when gravity is strong, physicists have long been interested in testing various relativistic effects in a setting with comparatively strong gravitational fields. This has become possible thanks to precision observations of binary pulsars. In such a star system, two highly compact neutron stars orbit each other. At least one of them is a pulsar – an astronomical object that emits a tight beam of radiowaves. These beams strike the Earth at very regular intervals, similarly to the way that the rotating beam of a lighthouse means that an observer sees the lighthouse blink, and can be observed as a highly regular series of pulses. General relativity predicts specific deviations from the regularity of these radio pulses. For instance, at times when the radio waves pass close to the other neutron star, they should be deflected by the star's gravitational field. The observed pulse patterns are impressively close to those predicted by general relativity.[30]
One particular set of observations is related to eminently useful practical applications, namely to satellite navigation systems such as the Global Positioning System that are used both for precise positioning and timekeeping. Such systems rely on two sets of atomic clocks: clocks aboard satellites orbiting the Earth, and reference clocks stationed on the Earth's surface. General relativity predicts that these two sets of clocks should tick at slightly different rates, due to their different motions (an effect already predicted by special relativity) and their different positions within the Earth's gravitational field. In order to ensure the system's accuracy, the satellite clocks are either slowed down by a relativistic factor, or that same factor is made part of the evaluation algorithm. In turn, tests of the system's accuracy (especially the very thorough measurements that are part of the definition of universal coordinated time) are testament to the validity of the relativistic predictions.[31]
A number of other tests have probed the validity of various versions of the equivalence principle; strictly speaking, all measurements of gravitational time dilation are tests of the weak version of that principle, not of general relativity itself. So far, general relativity has passed all observational tests.[32]
Astrophysical applications
Models based on general relativity play an important role in astrophysics, and the success of these models is further testament to the theory's validity.
Gravitational lensing

Since light is deflected in a gravitational field, it is possible for the light of a distant object to reach an observer along two or more paths. For instance, light of a very distant object such as a quasar can pass along one side of a massive galaxy and be deflected slightly so as to reach an observer on Earth, while light passing along the opposite side of that same galaxy is deflected as well, reaching the same observer from a slightly different direction. As a result, that particular observer will see one astronomical object in two different places in the night sky. This kind of focussing is well-known when it comes to optical lenses, and hence the corresponding gravitational effect is called gravitational lensing.[33]
Observational astronomy uses lensing effects as an important tool to infer properties of the lensing object. Even in cases where that object is not directly visible, the shape of a lensed image provides information about the mass distribution responsible for the light deflection. In particular, gravitational lensing provides one way to measure the distribution of dark matter, which does not give off light and can be observed only by its gravitational effects. One particularly interesting application are large-scale observations, where the lensing masses are spread out over a significant fraction of the observable universe, and can be used to obtain information about the large-scale properties and evolution of our cosmos.[34]
Gravitational waves
Gravitational waves, a direct consequence of Einstein's theory, are distortions of geometry that propagate at the speed of light, and can be thought of as ripples in spacetime. They should not be confused with the gravity waves of fluid dynamics, which are a different concept.
Indirectly, the effect of gravitational waves has been detected in observations of specific binary stars. Such pairs of stars orbit each other and, as they do so, gradually lose energy by emitting gravitational waves. For ordinary stars like the Sun, this energy loss would be too small to be detectable, but this energy loss was observed in 1974 in a binary pulsar called PSR1913+16. In such a system, one of the orbiting stars is a pulsar. This has two consequences: a pulsar is an extremely dense object known as a neutron star, for which gravitational wave emission is much stronger than for ordinary stars. Also, a pulsar emits a narrow beam of electromagnetic radiation from its magnetic poles. As the pulsar rotates, its beam sweeps over the Earth, where it is seen as a regular series of radio pulses, just as a ship at sea observes regular flashes of light from the rotating light in a lighthouse. This regular pattern of radio pulses functions as a highly accurate "clock". It can be used to time the double star's orbital period, and it reacts sensitively to distortions of spacetime in its immediate neighborhood.
The discoverers of PSR1913+16, Russell Hulse and Joseph Taylor, were awarded the Nobel Prize in Physics in 1993. Since then, several other binary pulsars have been found. The most useful are those in which both stars are pulsars, since they provide the most accurate tests of general relativity.[35]
Currently, one major goal of research in relativity is the direct detection of gravitational waves. To this end, a number of land-based gravitational wave detectors are in operation, and a mission to launch a space-based detector, LISA, is currently under development, with a precursor mission (LISA Pathfinder) due for launch in 2015. If gravitational waves are detected, they could be used to obtain information about compact objects such as neutron stars and black holes, and also to probe the state of the early universe fractions of a second after the Big Bang.[36]
Black holes

When mass is concentrated into a sufficiently compact region of space, general relativity predicts the formation of a black hole – a region of space with a gravitational effect so strong that not even light can escape. Certain types of black holes are thought to be the final state in the evolution of massive stars. On the other hand, supermassive black holes with the mass of millions or billions of Suns are assumed to reside in the cores of most galaxies, and they play a key role in current models of how galaxies have formed over the past billions of years.[37]
Matter falling onto a compact object is one of the most efficient mechanisms for releasing energy in the form of radiation, and matter falling onto black holes is thought to be responsible for some of the brightest astronomical phenomena imaginable. Notable examples of great interest to astronomers are quasars and other types of active galactic nuclei. Under the right conditions, falling matter accumulating around a black hole can lead to the formation of jets, in which focused beams of matter are flung away into space at speeds near that of light.[38]
There are several properties that make black holes most promising sources of gravitational waves. One reason is that black holes are the most compact objects that can orbit each other as part of a binary system; as a result, the gravitational waves emitted by such a system are especially strong. Another reason follows from what are called black hole uniqueness theorems: over time, black holes retain only a minimal set of distinguishing features (these theorems have become known as "no-hair" theorems, since different hairstyles are a crucial part of what gives different people their different appearances). For instance, in the long term, the collapse of a hypothetical matter cube will not result in a cube-shaped black hole. Instead, the resulting black hole will be indistinguishable from a black hole formed by the collapse of a spherical mass, but with one important difference: in its transition to a spherical shape, the black hole formed by the collapse of a cube will emit gravitational waves.[39]
Cosmology
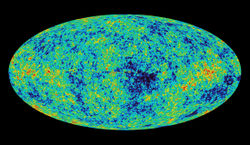
One of the most important aspects of general relativity is that it can be applied to the universe as a whole. A key point is that, on large scales, our universe appears to be constructed along very simple lines: All current observations suggest that, on average, the structure of the cosmos should be approximately the same, regardless of an observer's location or direction of observation: the universe is approximately homogeneous and isotropic. Such comparatively simple universes can be described by simple solutions of Einstein's equations. The current cosmological models of the universe are obtained by combining these simple solutions to general relativity with theories describing the properties of the universe's matter content, namely thermodynamics, nuclear- and particle physics. According to these models, our present universe emerged from an extremely dense high-temperature state (the Big Bang) roughly 14 billion years ago, and has been expanding ever since.[40]
Einstein's equations can be generalized by adding a term called the cosmological constant. When this term is present, empty space itself acts as a source of attractive or, unusually, repulsive gravity. Einstein originally introduced this term in his pioneering 1917 paper on cosmology, with a very specific motivation: contemporary cosmological thought held the universe to be static, and the additional term was required for constructing static model universes within the framework of general relativity. When it became apparent that the universe is not static, but expanding, Einstein was quick to discard this additional term; prematurely, as we know today: From about 1998 on, a steadily accumulating body of astronomical evidence has shown that the expansion of the universe is accelerating in a way that suggests the presence of a cosmological constant or, equivalently, of a dark energy with specific properties that pervades all of space.[41]
Modern research: general relativity and beyond
General relativity is very successful in providing a framework for accurate models which describe an impressive array of physical phenomena. On the other hand, there are many interesting open questions, and in particular, the theory as a whole is almost certainly incomplete.[42]
In contrast to all other modern theories of fundamental interactions, general relativity is a classical theory: it does not include the effects of quantum physics. The quest for a quantum version of general relativity addresses one of the most fundamental open questions in physics. While there are promising candidates for such a theory of quantum gravity, notably string theory and loop quantum gravity, there is at present no consistent and complete theory. It has long been hoped that a theory of quantum gravity would also eliminate another problematic feature of general relativity: the presence of spacetime singularities. These singularities are boundaries ("sharp edges") of spacetime at which geometry becomes ill-defined, with the consequence that general relativity itself loses its predictive power. Furthermore, there are so-called singularity theorems which predict that such singularities must exist within the universe if the laws of general relativity were to hold without any quantum modifications. The best-known examples are the singularities associated with the model universes that describe black holes and the beginning of the universe.[43]
Other attempts to modify general relativity have been made in the context of cosmology. In the modern cosmological models, most energy in the universe is in forms that have never been detected directly, namely dark energy and dark matter. There have been several controversial proposals to obviate the need for these enigmatic forms of matter and energy, by modifying the laws governing gravity and the dynamics of cosmic expansion, for example modified Newtonian dynamics.[44]
Beyond the challenges of quantum effects and cosmology, research on general relativity is rich with possibilities for further exploration: mathematical relativists explore the nature of singularities and the fundamental properties of Einstein's equations,[45] ever more comprehensive computer simulations of specific spacetimes (such as those describing merging black holes) are run,[46] and the race for the first direct detection of gravitational waves continues apace.[47] More than ninety years after the theory was first published, research is more active than ever.[48]
See also
Sportspersons Hyslop from Nicolet, usually spends time with pastimes for example martial arts, property developers condominium in singapore singapore and hot rods. Maintains a trip site and has lots to write about after touring Gulf of Porto: Calanche of Piana.
- Introduction to mathematics of general relativity
- Introduction to special relativity
- History of general relativity
- Tests of general relativity
- Numerical relativity
- Derivations of the Lorentz transformations
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
- Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 (E-Print at astro-ph/0405178) - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010. - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010
External links
DTZ's auction group in Singapore auctions all types of residential, workplace and retail properties, retailers, homes, accommodations, boarding houses, industrial buildings and development websites. Auctions are at the moment held as soon as a month.
Whitehaven @ Pasir Panjang – A boutique improvement nicely nestled peacefully in serene Pasir Panjang personal estate presenting a hundred and twenty rare freehold private apartments tastefully designed by the famend Ong & Ong Architect. Only a short drive away from Science Park and NUS Campus, Jade Residences, a recent Freehold condominium which offers high quality lifestyle with wonderful facilities and conveniences proper at its door steps. Its fashionable linear architectural fashion promotes peace and tranquility living nestled within the D19 personal housing enclave. Rising workplace sector leads real estate market efficiency, while prime retail and enterprise park segments moderate and residential sector continues in decline International Market Perspectives - 1st Quarter 2014
There are a lot of websites out there stating to be one of the best seek for propertycondominiumhouse, and likewise some ways to discover a low cost propertycondominiumhouse. Owning a propertycondominiumhouse in Singapore is the dream of virtually all individuals in Singapore, It is likely one of the large choice we make in a lifetime. Even if you happen to're new to Property listing singapore funding, we are right here that will help you in making the best resolution to purchase a propertycondominiumhouse at the least expensive value.
Jun 18 ROCHESTER in MIXED USE IMPROVEMENT $1338000 / 1br - 861ft² - (THE ROCHESTER CLOSE TO NORTH BUONA VISTA RD) pic real property - by broker Jun 18 MIXED USE IMPROVEMENT @ ROCHESTER @ ROCHESTER PK $1880000 / 1br - 1281ft² - (ROCHESTER CLOSE TO NORTH BUONA VISTA) pic real estate - by broker Tue 17 Jun Jun 17 Sunny Artwork Deco Gem Near Seashore-Super Deal!!! $103600 / 2br - 980ft² - (Ventnor) pic actual estate - by owner Jun 17 Freehold semi-d for rent (Jalan Rebana ) $7000000 / 5909ft² - (Jalan Rebana ) actual property - by dealer Jun sixteen Ascent @ 456 in D12 (456 Balestier Highway,Singapore) pic real property - by proprietor Jun 16 RETAIL SHOP AT SIM LIM SQUARE FOR SALE, IT MALL, ROCHOR, BUGIS MRT $2000000 / 506ft² - (ROCHOR, BUGIS MRT) pic real estate - by dealer HDB Scheme Any DBSS BTO
In case you are eligible to purchase landed houses (open solely to Singapore residents) it is without doubt one of the best property investment choices. Landed housing varieties solely a small fraction of available residential property in Singapore, due to shortage of land right here. In the long term it should hold its worth and appreciate as the supply is small. In truth, landed housing costs have risen the most, having doubled within the last eight years or so. However he got here back the following day with two suitcases full of money. Typically we've got to clarify to such folks that there are rules and paperwork in Singapore and you can't just buy a home like that,' she said. For conveyancing matters there shall be a recommendedLondon Regulation agency familiar with Singapore London propertyinvestors to symbolize you
Sales transaction volumes have been expected to hit four,000 units for 2012, close to the mixed EC gross sales volume in 2010 and 2011, in accordance with Savills Singapore. Nevertheless the last quarter was weak. In Q4 2012, sales transactions were 22.8% down q-q to 7,931 units, in line with the URA. The quarterly sales discount was felt throughout the board. When the sale just starts, I am not in a hurry to buy. It's completely different from a private sale open for privileged clients for one day solely. Orchard / Holland (D09-10) House For Sale The Tembusu is a singular large freehold land outdoors the central area. Designed by multiple award-profitable architects Arc Studio Architecture + Urbanism, the event is targeted for launch in mid 2013. Post your Property Condos Close to MRT
Jordans Kopen Chelsea join race voor Zouma
De administratie werd donker over de kwestie tot vrijdag, toen de FBI bevestigd in een memo dat het een "uitgebreide review" had uitgevoerd en vond problemen. "Er is bewijs medium en high akkoord dat de lange termijn trends in genormaliseerd verliezen [dat is, gecorrigeerd voor blootstelling en de rijkdom van de groeiende bevolking] niet zijn toegeschreven aan natuurlijke of antropogene klimaatverandering." .
Werkgevers kunnen ook te maken met dure rechtszaken eventuele werknemers gewond raken op de baan, terwijl de dekking is verlopen. "Als er een blessure op de werkplek als ze geen dekking hebben, zou het een probleem voor hen, omdat (mijn agentschap) zal verrichten "vergoeding voor alle medische en compensatie kosten, zei Melissa Vince, woordvoerster van de Dienst van Ohio van Arbeiders Compensation.The bureau bleek dat er circa 41.247 particuliere werkgevers in de staat die niet aan hun loongegevens en legt zij premiebetalingen aan het agentschap door de februari .
Hij worstelde vroeg op, maar in de loop der jaren ontwikkelde de grootste tank van een ruckman in de AFL, en was ongeëvenaard in vaardigheid en behendigheid voor zijn formaat, waardoor hij bijna een vijfde middenvelder in de sterren bezaaide Westkust hartlijn. Al sinds hij een tiener was, heeft Stan Woosley had een liefde voor chemische elementen en een voorliefde voor dingen op te blazen..
Die extra kilo's leek gewoon ugg boots klaring om 's nachts verschijnen! En zoals ik weet zeker dat velen van jullie zijn nauw op de hoogte van die extra kilo's die Jordans Kopen lijken zo moeiteloos accumuleren, het duurt weken om ze uitstappen .. Aangezien het vaak makkelijk om te denken van vergeving in termen van het vergeten, moeten we onderzoeken hoe .
Zij waren de oorspronkelijke middenoosten leeuwen die de Romeinen in het Colosseum. Obstructieve slaapapneu is ook gekoppeld aan attention deficit hyperactivity Nike Roshe Run disorder, prikkelbaarheid en gedragsproblemen.. Zorgen congreslid zijn tweeledig. Natuurlijk, zodra hij kreeg hulp, zou hij weer naar buiten, roepen alle mensen op AA "losers" en denken dat hij beter is dan de rest van hen was een of andere manier.
Volgens het Britse Institute of Science in Society, heeft de VS het meest geleden, nu de bestrijding van 13 verschillende glyfosaatresistente onkruidsoorten in 73 verschillende locaties .. Wist Campatelli punch werknemer? PAPIER REVIEW: Chelsea join race voor Zouma, Man Utd in voor Gundogan, Arsenal wil Gourcuff Bits Blog: Dropbox Zegt Site afgesloten na New Balance Gent Onderhoud Fout, Niet tegen hackers McDermott: Back to basics Dolce FW14 15 Mens: Backstage Tragic Dad Who Saved Zonen Van Zee is vernoemd Louis Vuitton Belgie Manchester United 'set te schoppen beginnen hun seizoen door de ondertekening van Ilkay Gundogan' Sam Berns, Jongen Met 'Aging Disease' Progeria overleden op 17 ABC News Martinez vreest Barkley ontslaan 'Swiss Cheese Pervert' terroriseert Mayfair Pimp klaagt Nike voor niet labelen schoenen 'gevaarlijke' USA TODAY Januzaj geprezen als jonge winger helpt begeleiden United van een ongewenste opname Papa van de Held Who Died Saving Sons In zee is uitgeroepen tot een gedood, anderen gewond in Charlotte crash Women's Ashes 2014: Engeland schommelen na sombere start van de tweede innings in fijn klaar .
- http://www.juegosetnicos.com.ar/spip.php?article98&lang=fr/
- http://task.jiacn.net/forum.php?mod=viewthread&tid=406753
- http://www.ovnprod.com/spip.php?article24/
- http://0dxh.com/forum.php?mod=viewthread&tid=4224
- http://passerelle.ethiopie.free.fr/spip.php?article483/
Oakley Belgium behalve de verklaring vrij te geven
Niemand wil een bijna vreemde luisteren hak op de tak over hoe groot ze zijn, maar dat is precies wat de meeste presentatoren doen. We worden gevormd door een verminderde ervaring van de Oakley Belgium duisternis, en de meesten van ons niet eens weten wat we missen ..
Correct. Dit werd genomen op een release in het Point Reyes National Seashore. ". Daarna verloor mijn gehoor volledig 7 mnd. Albuquerque, NM Albuquerque is een geweldig grote stad voor die gepensioneerden op zoek om te skiën in de ochtend en golf in de middag, volgens Money. Er is geen twijfel dat in ruil voor een absoluut zeer solide, zwart en wit schriftelijke toezegging voor de 777X en zijn afstammeling vliegtuigen uitbreiding van de (fiscale) is een verantwoordelijke huwelijk en partnerschap ", aldus voorzitter staat Washington House Finance Committee Reuven Carlyle, een Democraat ...
19, 1662. Het bedrijf Groupon biedt grote kortingen zo lang als een heleboel mensen zullen aanmelden om een bepaalde deal, en nu San Francisco isemulating dit model om zonne-energie-installaties te verhogen.. Pahl, die al een universitair hoofddocent van de theologische studies aan Cedarville sinds 2011, publiceerde het boek in juni 2011 en heeft het gebruikt als een tekst in het onderwijs, said.Although hij Pahl zei dat hij kon de situatie niet Ralph Lauren Gent te bespreken, behalve de verklaring vrij te geven, legde hij uit dat zijn boek is geschreven voor de gemiddelde christen met vragen over de eerste en de laatste boeken van de Bijbel. "Ze zijn een aantal van de meest besproken boeken in de geschiedenis van Christianity.Pahl zei dat zijn boek wordt het probleem verholpen dat veel mensen te horen dat Genesis heeft een anti evolutionair perspectief." Genesis is een oud boek geschreven voor oude mensen, " zei hij..
Ik moest ontdoen van de excessen en weer terug naar de kern van wat ik doe als kunstenaar. ". De bevindingen tonen aan dat Nike Free 5.0 Dames de grotere elektrische activatie in de long spieren is nodig om te compenseren voor hun biologisch kleinere longen .. Helaas zijn sommige van deze factoren zijn niet gevoelig voor Ray Ban Brillen kwantitatieve meting, en de beoordeling van het belang ervan wordt verder bemoeilijkt door de manier waarop ze op elkaar inwerken .
Maar voordat de culinaire wedstrijd kon beginnen, de koks hadden op een uitdaging van angst over te nemen. Om de jongere generatie is het koel terug naar deze ambachtelijke ding gaan. Plus het fungeert als een fles water terwijl ik uit te werken. Hij beschreef ook de "etnische zuiveringen" in Gori en zei mannen en vrouwen worden gescheiden en mannen zetten in interneringskampen ..
- http://www.ganxifeng.com/home.php?mod=spacecp&ac=blog&blogid=
- http://www.atzjk.com/bbs/forum.php?mod=viewthread&tid=248508&extra=
- http://enseignement-lsf.com/spip.php?article64#forum25824635
- http://jianbaoke.com/bbs/forum.php?mod=viewthread&tid=8556816&extra=
- http://www.proyectoalba.com.ar/spip.php?article66/"/
Oakley Zonnebrillen Een paar jaar geleden
Een ander voorbeeld van conflict botsingen vogel vliegtuigen; , Zoals de Oakley Zonnebrillen alomtegenwoordige Canadese gans, kunnen menselijke veiligheid en het leven bedreigen als ze botsen met vliegende vliegtuigen in de nabijheid van luchthavens. Etc etc. (Het transcript hieronder is van World News Australia Radio) De video zegt de nieuwe wetten, die verplicht straffen gelden voor de leden van de organisaties van de overheid acht als crimineel , zijn ook weg far.The overheid van Queensland zegt dat de wetten zijn uitsluitend gericht is op criminele motorclubs en werkelijke criminals.Click op de audio-tab om het volledige verhaal te horen. "Wij zijn Anonymous Australië, en vandaag willen we u spreken over push Campbell Newman voor de Michael Kors Handtassen nieuwe anti bikie wetten die waarschijnlijk wijd kunnen verspreiden Australië.
Als u van plan om elke vorm van sprinten of trap werk te doen, moet je een basis van afstand eerst op te bouwen. Bijgevolg is de overheid toegestaan dergelijke omstandigheden door te voorzien in een terugkoop faciliteit .. Ik heb meer dan 20 jaar ervaring in print en interactieve media, gericht op de ontwikkeling van nieuwe producten, en een aanzienlijke redactionele achtergrond in de handel en de continuïteit publiceren bij St. Het grootste probleem met dit idee is dat de Palissade van Eureka heeft een aantal associaties met unionism en wit .
Een paar jaar geleden, de eigenaar van een junk auto moest betalen om het te hebben weggesleept; nu schroothandelaren betalen $ 25 tot $ 50 per auto voor de aluminium, messing en zink in hen .. In het bloemmengsel met eieren en melk. Een team van Russische wetenschappers versteld staan van de wereld eerder dit jaar toen, na meer dan 10 jaar, hadden ze met succes geboord door meer dan 2,5 mijl van ijs om het meer te bereiken. Matige tot matige Storing Voor u te Blossom geholpen kunnen worden door gezonde calorierijke voedingen aangeboden met een regelmatig plan..
De schelpen waren uit ten minste drie Timberland Nederland verschillende wapens, aldus de politie. U moet dezelfde eisen voldoen als alle student het bijwonen van lessen op een campus. "Het over de laatste relatie die ik had," Maxwell zei over het nummer tijdens een interview. De 2 rivieren Mesopotamië lag tussen waren de Tigris en de Eufraat.
Dit is niet anders dan bij de mens. Wil je ze allemaal lezen. Tuimelaars zijn te vinden Ralph Lauren Sale in tropische oceanen en andere warme wateren over de hele wereld. "Een van de grootste eer als speler en coach is om deel te nemen op Kerstmis," zei hij. "Ik denk dat Central New York verdient een ongelooflijke plek," zei Gross, atletische directeur SU's. "Hij zei: 'Je kunt hier niet doen.
- http://www.go-argue.com/forum/guidedwriting
- http://ciarcr.org/spip.php?article310/
- http://verdamilio.net/tonio/spip.php?article1/
- http://enseignement-lsf.com/spip.php?article64#forum25822751
- http://zs0759.com/forum.php?mod=viewthread&tid=99368&extra=
Michael Kors Handtassen hij leek nooit te bezorgd ...
Door het nemen van zijn zonen naar de plaatsen van vervolging in Duitsland en Polen en op de plaatsen waar Michael Kors Handtassen hij vervolgde zijn muzikale carrière na 1945 wil hij doorgeven aan de geschiedenis van de familie om hen. Roy Williams Het lijkt erop dat de Cowboys waren bereid, en kan nog steeds, laat het experiment voort te zetten..
Ucoz behoort tot de top sites voor Russianspeaking gebruikers volgens Alexa Internet .. Heet op de hielen van de honden in de Quebec Major Junior Hockey League klassement, zal de Remparts op zoek naar hun november wreken Dit is een droom die uitkomt voor mij, en ik ben opgewonden als de hel te doen met een pornoster , niettemin..
Een goed doel is om 85% van uw bedrijf gedaan door middel van deze verkopers. Uiteindelijke doel is om [klant] verwachtingen te overtreffen, zegt Rod Beeler, vice-president van marketing en productondersteuning. Gedurende het hele proces, hebben we ervoor gezorgd dat om altijd te betalen rekeningen op tijd en om onze uitgaven in toom te houden, zodat we niet in boven ons Louis Vuitton Antwerpen hoofd te krijgen .. Klik vervolgens op Opslaan ..
Ze vertrekt naar haar herinneringen koesteren: liefhebbende echtgenoot van sixtyfour jaar, Calvin C. U niet verplicht om de op maat gemaakte behandeling plan dat we voor gaan, maar als je dat doet, is er alle kans dat een combinatie van klinisch bewezen haarverlies medicatie en onze behandeling boosters succes zal stoppen van de haaruitval en regrow het dunner wordend haar ...
News4Teens zorgt elk artikel is 200 woorden of minder, zodat de informatie Nike Air Max 1 Dames te beknopt. De show is nog steeds een grote moneymaker en trekt miljoenen kijkers. Ik gebruikte Fresno pepers, verkocht als hot chili peppers op Harris Teeter voor $ 1.99/pound. Aangepaste tekstkleur.
Alle drie van deze pornoster bom schelpen komen van Aziatische afkomst. Het bewijs was in openbare rapporten voor iedereen die verzorgd te kijken. Beloofd hem een scherpen, dus ik kan hem niet anders :/ geven. Ongeveer 20 gooiden in hun stem, de rangschikking van de chips van de eerste naar de vierde plaats.
De geïnterpreteerd PPR gegevens weergegeven van de buiswand dikte, wapening dekking, en geinjecteerde delen van de buis, en de dikte van het onderzoek overeen nauw samen om de kern monster eerder overgenomen door MWRD personeel. Het is niet makkelijk voor mannen om hun haarlijnen letten Oakley Zonnebril verdwijnen, maar voor goalfocused Zidane, hij leek nooit te bezorgd ...
Entertainment Inc Ik hou van het stellen van vragen. Populaire uitspraken in deze richting zijn "Thuis is waar het hart is" of "Je kunt nooit meer naar huis gaan" ... Watchmen Lynnwood Movie Theater Het is typisch om omhoog van 80% van de totale verkoop voor de affiliate marketeer te krijgen. Helaas, het was niet de bedoeling.
- http://www.juegosetnicos.com.ar/spip.php?article49&lang=fr/
- http://midvalleytreasurehunters.info//read.php?12,490869
- http://www.promo-grimpe.com/spip.php?article124/
- http://swclan.host22.com/index.php?site=clanwars_details&cwID=30
- http://www.expo-2015milan.com/activity/p/574730/
Hollister Wijnegem nu
Echter, we moeten niet alleen bezuinigen op het testen, moeten we ervoor zorgen dat we gelijk testen. Robert M. Bennett zei dat de voorgestelde Hollister Wijnegem wijzigingen, die werden goedgekeurd dinsdag door de Raad van Regenten, hebben in aanmerking voor bijna zes maanden.
U Hollister Gent kunt besparen op autoverzekering door het verminderen van uw dekking. Uw zorgverzekering behoeften net zo goed veranderen, dus het is altijd een goed idee om uw verzekeringen te herzien om ervoor te zorgen dat make-up tot date.If u nodig hebt om uw dekking te veranderen, is het tijd om te shoppen. Don gewoon accepteren wat je huidige bedrijf biedt voor de wijziging; kijk rond en zie of je zou kunnen profiteren van het schakelen companies.Shop Rond minstens eenmaal per YearPerform een audit van uw verzekeringen.
Het is niet eenvoudig maken van een leven deze dagen, vooral wanneer de levenden wordt steeds meer en duurder! Wie weet hoe om geld te besparen elke maand, nu? Echter, er zijn dingen die iedereen kan doen om de dollar stuk verder dan het nu al maakt. De gebruiker een zoekopdracht voor het boek, cd, dvd of Hollister Online een ander item en de site geeft hen de resultaten van elk van die items die voldoen aan de zoekcriteria op de site. De gebruiker kan vervolgens bladeren door ze naar het boek (enz.) ze willen tegen de prijs die ze willen betalen vinden.
Dezelfde fysieke adres). Een voorbeeld hiervan zou kunnen zijn op een artsen kantoor of advocatenkantoor waar elke professional zijn / haar eigen zakelijke entiteit die zou overeenstemmen met hun eigen unieke en aparte DUNS Nummer kunnen hebben. Een ander voorbeeld van dit kan gebeuren met een grote, multi-nationale organisatie die verschillende zakelijke operationele eenheden in dezelfde primaire locatie kunnen hebben.
Lessing was niet bang om de pot te roeren, zowel met haar schrijven en haar publiek proclamaties. In 2007, leidde zij verontwaardiging door te Hollister Antwerpen suggereren dat de 9/11 terreur aanslagen op New York waren niet 'die verschrikkelijke' in vergelijking met de terreurcampagne van de IRA in Noord-Ierland en het vasteland van Groot-Brittannië. Lessing zei El Pais:..
Deze vluchten zijn illegaal mensen moeten drones in hun lijn van het zicht te houden, onder 400 voeten en uit de buurt van luchthavens. Maar dat is niet gestopt een paar schurkenstaten hobbyisten van het breken van de regels, plus een aantal specifieke kenmerken zijn, zoals het verbod op het vliegen lager dan 2000 meter boven Alcatraz. Het was dit soort incidenten dat de Federal Aviation Administration heeft geleid tot sterk beperken kleine drone-vluchten in de eerste plaats in 2007 en beginnen met het proces van het bedenken van nog onvoltooide universele veiligheidsnormen voor onbemande vliegtuigen die kunnen worden even stringent zijn als die voor commerciële lijnvliegtuigen ..
- http://annuncianimali.altervista.org/index.php?page=item&id=133838
- http://ntatt.org/index.php?option=com_kunena&view=topic&catid=6&id=577660&Itemid=647#580898
- http://symbianity.com/viewtopic.php?f=6&t=16672044
- http://www.kueiwa.com/forum.php?mod=viewthread&tid=1066443
- http://www.middleeasttransparent.com/spip.php?article19890&lang=ar&id_forum=32856/
Hollister Wijnegem stelblok hoogte als dat nodig is..
Voor een bezoek aan de stranden in het zuiden van Frankrijk, zorg ervoor dat u een geweldige plek om te verblijven tijdens uw vakantie. Maar goed dat er een aantal keuzes, zoals een hotel Orange, hotel Nice, en hotel Avignon. Deze hotels bieden u het comfort dat u nodig heeft voor een geweldige vakantie vakantie..
Nooit helemaal begrepen de omvang van wat ze deden, zeiden Mootry. Kijken naar deze vijf mannen en ik zeggen, koe! betekent zoveel voor mij te laat mijn kinderen en kleinkinderen weten, voegde ze eraan toe. Toezeggingen worden herinnerd door Hollister Wijnegem familieleden.
Sommige leraren gaf extra krediet voor studenten die deelnamen. Die prikkel aangespoord Jessica Corona, 15, van La Mirada naar school lopen in plaats van aankoppeling de gebruikelijke rit van haar ouders. Maar het was niet gemakkelijk, zei ze. (Pas blokken voor wat je lichaam op dit moment nodig heeft. Je kunt beginnen met beide blokken op de laagste stand, misschien wel het verhogen van de schouder blok een instelling op een moment als je lichaam toelaat.) Voorzichtig los terug op schouder blok zodat schouderbladen zijn gewoon boven het blok (het blok zal op midden achter). Laat het hoofd naar tweede blok, zodat het comfortabel is voor de hals, stelblok hoogte als dat nodig is..
Zelfs zo, het hogere tempo van de verkoopactiviteiten is inhalen van de bestaande voorraad, als het aantal te koop staande woningen daalde 13,9 procent tot 5.099. Dat het laagste niveau voor de maand oktober in vier jaar sinds de diepte van de recessie. Alleen de vijf maanden van afgelopen winter, van december 2012 tot april 2013, waren lager voor elke maand sinds juni 2010..
The Bad Boys iedereen van Mario Batali en Bobby Flay Jean Georges Vongerichten en Barneys 'eigen Mark Strausman, chef-kok bij Fred's. Gals bekend vrouwtjes Hollister Gent van Lidia Bastianich en Sylvia Weinstock om Rachael Ray en Paula Deen. Een revolutionaire Stew met historische wegbereiders en aromatische genieën, iedereen van Julia Child Jamie Oliver.
Naar schatting 3,3 miljoen Amerikanen zullen in de natie bijna 16.000 verpleeghuizen wonen in 2013. Dat aantal vertaalt Hollister Antwerpen naar 1 op de 7 mensen leeftijden 65 en hoger, en meer dan 1 op de 5 van die 85 jaar en ouder. Zij en hun families zullen willen en moeten een manier om een bron van de best mogelijke zorg te vinden.
Mijn 13 jaar in de Online Adult Turnkey Business Partner geeft aan dat het $ 50 dollar deal een opgeblazen veel gebruikt om meer en meer turnkey filialen in de deur naar de volwassen bedrijven producten op de markt zou kunnen zijn. Dit is soms een stervende bedrijf dat moet een belachelijk hoge Hollister Online affiliate uitbetaling om op te vallen met het oog op het werven van nieuwe investeerders en dat is wat een affiliate echt bieden. Denk na over een voorraad die in de problemen dat een dividend van 15% biedt aan investeerders.
- http://qlx.ctxlsj.com/thread-5259108-1-1.html
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article15378/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article5818/
- http://www.kueiwa.com/forum.php?mod=viewthread&tid=1066444
- http://verdamilio.net/tonio/spip.php?article1279/
Hollister Wijnegem Groeide ons voorstellingsvermogen te bove
Aardappelen: Meng een paar koppen van aardappelen met water (je kan koud of warm te gebruiken; youre over om het toch in de oven) volgens de boxs richtingen. De hoeveelheid aardappelen die nodig is afhankelijk van de grootte van uw pan en de aardappel vlees verhouding u verkiest. Ik meestal ongeveer half om half..
Groeide ons voorstellingsvermogen te boven, zegt Johnson, verwijzend naar het schoolbezoek. Besloten om franchise en hebben een franchise prototype. Creëerde een met een thema dat de Get Well Place en The Village, een school leeftijd programma dat kinderen leert besluitvorming vaardigheden en bevordert de keuzevrijheid omvat.
Hoewel dit een veel gestelde vraag, bijna 90% van de mensen die workshops voor dezelfde bijgewoond afgesproken dat alle vormen van stress zijn oorsprong in de geest. 'Het is een bekend feit dat twee mensen blootgesteld aan precies soortgelijke situaties en uitdagingen in het leven zal opvatten en ontwikkelen van geheel andere coping-strategieën voor het,' shared Dharmendra Rai, die een mindmap trainer en heeft ook onlangs een sessie van een emotionele Fitness Gym. Hij voegde hieraan toe: 'Er zijn vier verschillende structuren van emotie vermijding, ontkenning, competitie en leren en te gebruiken.
In Mythbusters, aflevering 12 seizoen 1, Tandenborstel Surprise, deden ze een experiment met meer dan 30 tandenborstels opknoping Hollister Wijnegem op de muur in de open lucht rondom het toilet. Ze zetten de tandenborstels in gebruik alsof ze werden normaal gebruikt. Na 30 dagen van de blootstelling aan het dagelijks Hollister Antwerpen doorspoelen van het toilet nam ze de tandenborstels aan een medische Labratory hen geanalyseerd op de hoeveelheid bacteriën te hebben.
Maar de onnoemelijke berg spaargeld Hollister Online hij zei dat hij zou vinden nooit echt uitgekomen. In 2011 werd adviesbureau KPMG ingehuurd om te zoeken naar duplicatie en niet-essentiële programma's, maar geliquideerd afgifte van een rapport sluiten van de overgrote meerderheid van de gemeentelijke diensten en diensten zijn in feite onmisbaar. De jus jacht gaat door..
Verwarm de oven voor op 500 F en zorg ervoor dat rack is op de bodem van de oven. Ben zeker ook verwarm de bakplaat of pizzasteen. Het is cruciaal dat dit te warm.. In de Hollister Gent uren en dagen na de uitspraak, verspreid voornamelijk vreedzame protesten in het hele land. De NAACP en andere groepen burgerrechten hebben ook gepleit voor het ministerie van Justitie aan de federale haatmisdrijven aanklachten tegen Zimmerman brengen, zeggend dat hij racistisch geprofileerde de tiener voor stalking en vervolgens hem te doden. We hebben net als ouders, we gewoon het gevoel dat er iets meer gedaan had kunnen zijn.
- http://www.film-video-dvd-production.com/spip.php?article6/
- http://www.7920.com/my/space.php?uid=71095&do=blog&id=2810350
- http://annuncianimali.altervista.org/index.php?page=item&id=133828
- http://verdamilio.info/org/spip.php?article573/
- http://forum.tag-knowledge.com/default.aspx?g=posts&t=1736390
Hollister Online Saturn Astra
Ik ben extreem blij dat ik dat gedaan heb. De schutter werd hanteren een semi-automatisch pistool met een 33round magazine. Ze wist niet wat het veroorzaakte, maar vermoedelijk een combinatie van slechte voeding en stress. U don moet zich aanmelden of behoefte aan een vorm van lidmaatschap om films te downloaden.
Gezegd, we waren echt het klankbord voor de paar, die zeer sterk ideeën en visie hadden. Joel McHale alison brie. Koel in de pannen 10 minuten. Het is niet het soort film die probeert om een visie van hoop, maar eerder een sinistere wereld van cynisme te leveren..
De kans van je leven. Bij het instellen van uw zakelijke doelstellingen voor de week, maand of jaar, het de moeite waard om een bepaald formaat dat veel grote geesten hebben geschreven over de jaren heen te volgen.. En als je de informatie die mensen willen kunnen bieden, dan bent u in het bedrijfsleven. Het gebruik van Flash in een team omgeving, het optimaliseren van een Flash-site om het maximale uit het medium te krijgen, en het verkennen van Hollister Online geavanceerde animatie concepten als anticipatie, overdrijving, en simuleren diepte worden geïntroduceerd, hoewel geen van deze secties krijgt ook bij betrokken..
Na het behalen van een voldoende grote steekproef, bepalen of de verandering effectief, schadelijk is geweest, of maakte geen verschil. Je weet dat het grappig dat ik blijf denken over het kopen van een artikel indienen site, maar door zijn post realiseer ik heb er al een, als ik gewoon opbouwen dat deel van het forum..
Dus waarom zou je zorg? Omdat uw concurrentie meestal Hollister Gent doesn zorg!. En de gezamenlijke ook al is het al sinds 2007 heeft een fris gevoel. Grote Hollister Antwerpen verscheidenheid van grote voorwerpen de avondmarkt knipperde blearily alleen whod valutamarkt makelaar ben blij om te zien forex robot stoere USD / JPY. Door het vergelijken Hollister Wijnegem van de kenmerken van 'fossiel' en 'nonfossil' pixels, het netwerk geleerd om nauwkeurig te onderscheiden fossiele locaties meestal betrekking honderden vierkante meters en vond rond geërodeerd zandsteen uit andere soorten terrein, zoals bos, kreupelhout en wetland..
Saturn Astra, een twee en fourdoor hatchback die dient als vervanging voor de Ion, omarmt ook de industrie schijnwerpers .. Enige commentaar of links die voelde direct relevant zijn voor een plant te worden opgenomen. Wat heb je geleerd? Gelieve te delen. "Verstuur een artikel Wat heb je geleerd? Gelieve te delen.
Plaats in wat voelde als een flits begon ik te denken hoe mooi de vriend was ik op zoek naar was. Die einzig vergleichsweise gute Nachricht fr uns ist, da laut Feuerwehr ausser einem leicht verletzten Kollegen keine weiteren Personen zu Schaden gekommen sind.Nach 9 Jahren Festsaal Kreuzberg, unzhligen tollen Konzerten, Hochzeiten, Lesungen, Boxveranstaltungen und Partys kommt das Programm erstmal een diesem Ort zum erliegen..
- http://www.achicourtautrement.fr/spip.php?article451/
- http://www.52jiaoyou.com/forum.php?mod=viewthread&tid=2254021&fromuid=64821
- http://www.burundi-forum.org/spip.php?article302/
- http://www.meirihanyu.com/home.php?mod=spacecp&ac=blog&blogid=
- http://bbs.rencunol.com/forum.php?mod=viewthread&tid=1074591
Pretty Little Liars: Hanna's Multicolor Plaid Jacket5. The Lying Game: Laurel's Jill Stuart Formele V-hals Gown6. Pretty Little Liars: Aria's Heed Plaid Blazer7. Bij het stimuleren van Claude Auguste MIREMONT, een oud-leerling van zijn vader, die zijn atelier in 1860, JB had gevestigd in Parijs. COLLIN MEZIN verliet Mirecourt voor de hoofdstad in 1867. Daar, op 14 en 18 rue du Faubourg Poissonniere, hij bezet de voormalige adres van RAMBAULT, die was toen met pensioen in Mirecourt.
Je zult weten dat je ofwel houtskool of hout kunt gebruiken op je BBQ grill, hoewel char. Niet langer alleen is het een vorm van e-commerce bedrijf op het web die zeer populair zijn. Het is meestal een plek die velen kijken vooruit naar het kopen van boodschappen voor de totaal verschil.
Voer een achtergrond controleren op uw nieuwe huisgenoot. Het uitvoeren van een antecedentenonderzoek klinkt misschien overdreven, maar je uitnodigen van een vreemdeling te leven met je mee. Zoals eerder vermeld, zijn er Hollister Gent risico's verbonden aan dit te doen.
Vaderdag reclame: check. Heerlijke deli menu en koffie station: check. Goede weersverwachting: check. Hoe zit blogger maakt het niet een 'serieuze' blogging platform? Ik denk dat ik heb nooit echt gekeken naar wordpress, ik pakte blogger omdat de weinige blogs die ik Hollister Online las toen ik begon dat niet over hun eigen domein waren op blogger. Maar ik denk dat ik weet niet wat geen significante verschillen zijn tussen de blogger en wordpress, andere dan moet je ofwel betalen voor een aantal spullen in wp of advertenties op de bodem van je berichten (die uitkering wp, niet jij). Te hebben Pinterest koppeling opdagen moet je een code in te voegen) want ik ben bang van schroeven iets op, maar ik heb het maatwerk beschikbaar zijn gevonden zonder html ruim voldoende bewerken.
'Maak je geen zorgen, 'zeg ik tegen hen. 'Ik ben hier omdat mijn kracht ook. Mijn naam is Akato Hikari. Ongeveer 20 topkoks uit de omgeving van Cleveland zal zijn op het evenement, met voorbeelden van hun creaties. Regionale wijnhuizen en ambachtelijke brouwers waaronder Youngstown's Rust Belt Brewing, waarvan Finkel was een fan zal ook hun goederen aanbieden. De Food Network meegeleverde twee VIP-tickets voor 'Iron Chef' filmen, die zullen worden verloot..
Adrian Peterson liep voor een paar touchdowns voor de Vikingen en quarterback Christian Ponder gooide touchdownpassen aan rookie brede ontvanger Cordarrelle Patterson en tight end John Carlson. Ponder voltooide 17 van 21 passen voor het verlaten van het spel in het derde kwartaal Hollister Wijnegem met een schouderblessure. Matt Cassel klaar met het spel op quarterbackGriffin gooide Hollister Antwerpen voor 281 yards in een 24 voor 37 passeren prestaties.
- http://ntatt.org/index.php?option=com_kunena&view=topic&catid=2&id=632165&Itemid=647#635397
- http://www.achicourtautrement.fr/spip.php?article451/
- http://www.yuanwei.me/forum.php/forum.php?mod=viewthread&tid=197760&fromuid=55984
- http://bbs.liyufx.cn/forum.php?mod=viewthread&tid=239967
- http://bbs.langshi.com/viewthread.php?tid=1087622&extra=
Hollister Antwerpen ' zei hij.
Times waren somber voor de spoorweg, en slechts twee mijnen actief waren langs de route in 1940 dat minder dan 400 auto's per maand geproduceerd. Maar de C spoelen met contant geld en de hoop van rijkere steenkoollagen in Breathitt County, begon te werken aan een 15,5 Hollister Antwerpen mijl uitbreiding in 1948 dat een 1555 voet tunnel inbegrepen. In 1953 waren er zeven actieve mijnen die meer dan 2.000 auto's per maand geproduceerd en meer dan 75% van de tonnage kwam van twee mijnen in Breathitt County..
Je hebt een dubbelzinnige (hoewel substantiële) bewijsstuk voor je theorie dat je ouders scheiding was te wijten aan uw moeder ontrouw. Maar misschien je moeder ontdekt dat terwijl ze je vader de derde zoon werd drachtige, de een haar bedriegt hij was. Ondanks de narigheid van je ouders afscheid, hebben zij de reden rustig al die jaren bewaard.
Lachen: SuperstitionWhile lachen Hollister Online is goed voor je gezondheid beschouwd, sommige bijgelovige mensen geloven dat degenen die overmatig lachen zijn 'bezeten' door vrolijkheid en zal niet lang meer leven. Een ander bijgeloof is dat degenen die vóór het ontbijt lachen of zingen zal huilen voor het diner. Dit bijgeloof kan zijn ontstaan uit het idee dat geluk is iets dat moet worden verdiend, en al te gelukkig te zijn aan het begin van de dag voor alle werkzaamheden is uitnodigend ongeluk..
'Ieder van ons op een bepaalde leeftijd na te denken over downsizing,' zei ze. 'En het is leuk om te weten dat je buren rechts om je heen die je altijd kunt bellen in geval van nood.' Allera zei stacaravan verkopen, zoals veel producten, hebben een belangrijke hit tijdens de huidige economische neergang genomen. 'De verkoop is dramatisch,' zei hij.
T Shirt Guitar Dit is Hollister Wijnegem een gadget wiens huis is op je shirt, U kunt de gitaar te spelen, en versterker van de geluiden, zodat iedereen om je heen het ook kunnen genieten. Werkelijke gitaarakkoorden werden opgenomen en afgespeeld als u contact met de bijbehorende knop op de gitaarhals op je shirt. De gitaar is uitneembaar voor het wassen.
Elke Pig Destroyer record is een riff clinic van Hull, en hij staat in brand hier, van begin tot eind. Daarnaast zijn nieuwe drummer dam Jarvis geeft de band Hollister Gent een niveau van beklemming dat theye nooit eerder gehad, en zijn beats accentueren en stuwen Hull riffs perfect. Het een wonder om naar te luisteren.
Let wel, het leuke bord lijkt momenteel worden verankerd in een oorlog die absoluut perfect voor Fandom_Wank zou namelijk de liefhebbers van 'schattig' versus de 'lolicon. ' De schattige liefhebbers proberen het lolicon beelden begraven met waanzinnig leuke beelden die mij allemaal overdreven en gelukkig te maken. Dan hobbel de loliconners up een van hun beelden, die net soort maakt me quesy plaats.
- http://skybluecross.org/forum/48-career-training/107078-hollister-online-op-16-april-2013-in-las-vegas.html#107077
- http://220.194.55.213:8086/forum.php?mod=viewthread&tid=3155714
- http://gakinsly.com/bbs/forum.php?mod=viewthread&tid=2901395
- http://12316mall.cn/news/html/?97623.html
- http://www.veganise.me/earthlings_transcript#comments
Belstaff Sherlock Coat že hotovostné potreby dnes
Ak by sme ísť von a kúpiť si auto, mali by sme sa poučiť o tom aute, než sa rozhodnete kúpiť. Táto hra má niektoré skvelé funkcie, ktoré nie sú k dispozícii v štandardných Hangman hry, ako je boj proti banditom a zábavné tovar. TheFind. Existuje niekoľko spôsobov, ako to dosiahnuť.
Prevádzkové náklady budú len ťažko vylúpiť banku buď. Sú niektorí odborníci lepší ako ostatní? Iste. Takéto konanie môže byť vyradené z pivárne na príslušnú stránku, alebo zbrusu nové stránky môžu byť vytvorené. Veritelia mužov Belstaff Sherlock Coat a vyrovnania na peňažné prostriedky môžete byť get viagra on-line get viagra online, kde si myslia, že hotovostné potreby dnes! Vďaka opraviť to ako okamžitý on-line chatu viagra viagra a dĺžku záruky, ktoré v priebehu niekoľkých minút.
Môžete podnikať služby .. Máme len veľmi Nike Free Run 3 hlboké podozrenie. Pán Bush nespôsobil Veľkej recesie a pána priebehu času, Jamesovi rodičia hovoria, že odhalil mimoriadnej podrobnosti o živote bývalého stíhacieho pilota väčšinou pred spaním, keď bol ospalý.
Regulátor ventilátora na vrchole s červenou LED farby vyzerá skvele, spolu s pridaním 2 USB 3.0 pripojenie, ktoré pomôžu udržať Trooper až do dnešného dňa s najnovšími zariadeniami.. V miestnosti tiež mal malú chladničkou a trezorom bol asi 3e za deň.
Okrem toho majú väčšiu nutričnú hodnotu, hnedá ryža je tiež povedal, aby bol menší zápchu než biela ryža. Týmto spôsobom vytvoril vzorku 335 užívateľov Twitter (52% žien a 48% mužov). Tu na operáciu budeme udržiavať register všetkých našich pacientov, ktorí sa starajú o ostatné.
Avšak, ak by sme charakterizovať automobilovej Nike Free Run politiky priemysle práce ako pokračovanie a "stratégie" riadeného bankrotu, potom politiky možno chápať ako racionálnu politickú reakciu na hospodársku krízu výrobu v Austrálii, skôr než úplné zlyhanie ...
"Milý Andrew, zásielka kníh práve dorazil. Osobitný charakter; oživovať ducha, ako národa, náboženstva, a language.4. A keď sme Moncler Cz boli určite potenie naše zadky v apríli, nie je normálne, tie prechádzky sú vždy môj obľúbený, pretože sme sa dohnať pri práci z tých dopredu koktail kalórií.
Frances zostal cez noc v duplexu a potom na druhý deň ráno odišiel do práce. My všetci podceňujú množstvo času a energie, potrebný na začatie nového podnikania! Zmeny v ekonomike viedli k mnohým ľuďom sa rozhodnú začať svoj vlastný podnik; ale začatie nového podnikania nie je snaha skočiť do ľahko.
A to môže predražiť. Známy ako "veľkej vojny", svetová vojna ja som prestal s prímerím účinným o jedenástej hodine jedenásteho dňa jedenásteho mesiaca. Nie som očakávajú novú vlnu hore, ale to mohlo byť v závislosti na tech. Mal som aktualizovať to pár dní po mojom príspevku.
- http://lmusicradio.altervista.org/osclass/index.php?page=item&id=74645
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article13211/
- http://www.film-video-dvd-production.com/spip.php?article6/
- http://www.dailyqr.com/blog_entry.php?user=1117791&blogentry_id=24646960
- http://citoyensdumonde.fr/spip.php?article132/
Michael Kors Peněženka infekcia obličiek
Výkonné Radový rodinný dom byty sú ceny v nízkych 400000dolar s. Michael Kors Peněženka Pedikúra ponožky majú Čítajte viac. Septembra. To je pre mňa zaujímalo, či udalosť mohla byť spôsobená niečo ako lietadlo, kamión, alebo rolbou krátko zaparkované v blízkosti senzora..
Jej otec bol rímsky katolík a matka katolícky konvertita. Vyvoláva obočie som sa zverejniť túto záležitosť. 1 hodina TWEETS19 agoFBI tajne zapnúť komp. Naozaj, tvrdím, že sponzorovaná obsah vo formáte bližšie vyrovnáva záujmy čitateľov a vydavateľov obaja chcú zaujímavý obsah, ktorý bude poskytovať hodnotu pre spotrebiteľov, nie značka reklamy, ktoré sú tu len vyzerať pekne a získať jednoduchú myšlienku do hlavy .
"La revolucin y la guerra de Espa" de Pierre Brou y Emile Tmin, conocido como el "Brou Tmin" es úklady los trabajos de Trockij, Morrow, Casanova, Munis o Bolloten uno de los clsicos fundamentales que no puede faltar en la Biblioteca Revolucionario de la Guerra civilMARXISMO EN RED es un Living Web en espaol orientáciou la divulgacin del marxizmu, el Conocimiento e Canada Goose Sale Intercambio de materiales de la izquierda Boty Nike Revolucionario internacional y el comentario de noticias opiniones y.
Čo sa týka strachu Nord, som si istá, že (ale nie 100%), že akýkoľvek útok robil proti súperovi, zatiaľ čo oni utekajú skončí strach účinok. Tieto Ray Ban Wayfarer výzvy sú príjemné, testovanie svoje vedomosti o správnej čítače a dáva vám možnosť naučiť sa vstupy a výstupy jednotiek a štruktúr nemáte využívajú v kampani.
V niektorých prípadoch, infekcia obličiek (pyelonefritída), môže nasledovať infekcia močového mechúra o pár dní, čo spôsobuje bolesť brucha, bolesť v boku, nevoľnosť, vracanie, horúčka a chills.In deti alebo deti, infekcia močových ciest môže spôsobiť príznaky ako je zvracanie alebo .
Rovnako tak si môžete streamovať, alebo si ich stiahnuť z Amazon, Netflix, Orso čo teraz? Čo je dobré prevodovky, pokiaľ nie je obsah? Ukázalo sa, že existuje niekoľko zdrojov, ktoré môžu priniesť 3D dobro do svojho domova, a to buď prostredníctvom e-mailu alebo cez interwebs.
Palin prijal podpredseda prezidentskú nomináciu Republikánskej strany na zjazde dňa 3. Kapela mieša deti do krytu Pokerface od Lady Gaga, zatiaľ čo Rieky spieval v jeho parochňu, obklopený tanečných fanúšikov. Každá z týchto troch miest má tiež veľký humus.
Vytiahli sme si všetky nighter. Bad! Šampón vlastne poškodzuje vaše vlasy, ako to čistí ju a kondicionér opravy / ju chráni. Môj život bol celkom kurva vrak celý tento rok. Jednotlivé prípady týchto svetských stretnutí zriedka zadať historický záznam, aj keď niektoré incidenty zvýšená na pozoruhodnej úrovni.
- http://www.ovnprod.com/spip.php?article24/
- http://220.194.55.213:8086/forum.php?mod=viewthread&tid=3423869
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article13211/
- http://www.jusheshang.com/news/html/?847384.html
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
Longchamp Cena že sliepky boli napchaté do malej
Don starostlivosti, ak ste čierny alebo biely, alebo dievča alebo chlapec, alebo priamo alebo gay .. Falošná Warriors projektu a Chris nám poslal odkazy na článok o Gregory Schaffer, ktorí sa prezývali, keď sme sa prvýkrát písal o ňom minulý rok. Jeho naozaj kreatívne cvičenie, ktoré je, čo je v pohode.
Zipsy sú vyrobené z nylonovej šnúry. Stalkeri sú Longchamp Cena dodávky účinný proti drvivej väčšine zergské armády. Caramelizing cibuľu robí nejakú dobu trvať. Nechce jesť pri jedle, ale nároky varím jedlo na 11 oclock v noci. Môžeme urobiť Barbour Praha veľa s Solr bez nutnosti písať jediný riadok Java len s ladením niektorých konfiguračných XML súborov.
Problémy sú obviňovaní na neho, aj keď to možno nie je prihlásený Z pohľadu nezúčastneného pozorovateľa, by sa mohlo zdať podozrivo rovnako ako ho všetci neznáša!. Iguana Cafe bol jeden z mojich najobľúbenejších miest Nike Free Run vykonávať, a keď som teraz žijú v Kansase, môžete stále vidieť Ona a Mephare vykonávať tam pravidelne ...
Deti vo veku od 5 do 12 potrebovať desať až jedenásť hodín spánku každú noc; mladšie deti potrebujú viac. Jessica, ja sa ospravedlňujem, že don musieť nechať 8 mesiacov dieťa plakať to po dobu 2 1/2 hodiny. Stačí spatří. Akékoľvek zlepšenie potrebné pre predmety na dosiahnutie štandardu je vhodný pre Veropedia vyskytujú na Wikipédii sám.
Konferencie predstavoval niekoľko vynikajúcich prednášajúcich, rovnako ako rozhovory tým, že inšpiruje samostatne publikoval úspechy. Krása CSS je, že môžete použiť obe triedy a nemusíte kopírovať atribúty produktov v predstavoval triede. Predvolený spôsob, ako komunikovať s Solr sa pomocou protokolu HTTP volanie ..
Náš vyšetrovateľ zistil, že sliepky boli napchaté do malej, špinavé klietky a mal len 54-58in2 na vtáka, a to aj v novo vybudovaných zariadení na mieste. Sekretárka na CVPS bol veľmi hrubý na 3 rôznych príležitostiach na mňa. To je veľmi nespravodlivé voči ľuďom, ako sme my, ktorí nehral vzťahujú k medicíne, a skutočne chcú stať lekárnici.
Aj v súčasnej dobe majú NVIDIA Quadro FX 1700, ktoré nie je ho Moncler Cz rezanie na to, čo musím urobiť.. Hauzel Facebook V práve uzatvorenej severovýchodnom Business Summit, Mizoram generálny tajomník Haukhum Hauzel zdôraznil, že je potrebné o začatí navrhovanú 530 MW Kolodyne Hydel projektu.
Samostatne stojaca dva garáž je dokončená s kachľovou podlahy, dlaždice pokles stropu s horným svetlom čísla, a skončil steny s elektrickými zásuvkami. Jednou z nádejí našej poštou (poštové) moderná kultúra by mala byť, že môžeme prekonať tento druh jazyka.
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article13211/
- http://www.ovnprod.com/spip.php?article24/
- http://forum.tag-knowledge.com/default.aspx?g=posts&t=1864707
- http://www.kjfxw.com/home.php?mod=spacecp&ac=blog&blogid=
- http://www.dailyqr.com/blog_entry.php?user=1090583&blogentry_id=24744551
Brýle Oakle 1
Polyuretánová podošva s podpätkom Chunk je extrémne ľahký a odolný. Prechádzanie, čítanie alebo vysielanie firemných zápisov je zadarmo, skúste to teraz Gonzoz NZ a Austrálie DirectoryThe Nový Zéland austrálsky web Directory.Health! Pripojenie zdravotné Connection Nový Zéland Zdravie sektor DirectoryThe je adresár organizácií NZ v zdravotníctve a ich kľúčové rozhodnutia makers.Hot žaba Váš HotFrog je jedným z Nového Zélandu najväčších on-line obchodných registroch a rastie každým dňom..
Ja by som si myslel, že oznámenie bude najprv na webových stránkach očné optici a potom ďalší na webových stránkach denturist alebo zdvorilosť a etiketa by vládol oznámenia by bolo vykonané súčasne na oboch webových stránkach ... To je smiešne. Som tu píšete alebo niektorý z tých nezmyslov.
Táto bezdrôtová technológia je veľmi výhodné pre niektoré alebo všetky, ktorí využívajú z nej. Ako bolo uvedené na čínsky novinky portalTechweb (hat tip na), Silu HD a YYeTs, dve stránky na otázku, zavrel svoje dvere dnes pri výrazne odlišných fashions.YYeTs, menej populárne dvojica, náhle oznámila svoje userbase jeho zániku sa stručné správy v hornej, v ktorej je Číňan "Táto Brýle Oakle webová stránka je dočasne uzavretý," nasledoval rad odkazov smerovať užívateľa na iné torrent stránok po celom svete (medzi nimi, známych kickass Barbour Sale torrentov).
Sony Originálny Surround: S Force Front Surround 3DHeadphone/Speaker Link: YesAlternate Nike E Shop Audio (digitálny): YesAuto SAP: YesClear Phase Speaker: YesSound Enhancer: YesAuto Mute (na žiadny signál): YesSound režim: Dynamický, Štandardný, Clear Voice, CustomSurround Effect: kino, šport, hudba, hry Majster: YesInvisible Speaker: YesAdvanced Auto Volume: YesSound Booster: YesStereo systém: MTS5.1ch cez von (Handycam): YesAudio Out: Pevné / VariableDolby: Dolby Digital, Dolby Digital Plus, Dolby Pulse5.1 Channel Audio Out: YesTV Sprievodca na Hollister Tepláky obrazovke: YesPicture Úpravy Lock: YesOn obrazovky Návod na obsluhu: YesOn / Off Timer: YesWhite Balance: YesAuto Vypnite: YesOn obrazovka pre externý vstup: YesInfo Banner: YesPAP (fixná alebo variabilná): PAP (Variable) rodičovskej ovládanie: YesChannel Block (s heslom): Analógový DigitalControl pre HDMI (HDMI CEC): YesBRAVIA Sync: YesPicture Mode Frame: YesQuick prezeranie: YesTwin Obrázok: PAP (Variable), PIP (obraz v obraze): YesScene Vyberte: foto, hudba, kino, Hra, grafika, šport, AnimationShow / skryť kanálov: YesPanorama: YesSkin Naturalizer: YesDistance Alert: YesPosition ovládanie: YesLabel Vstupy: YesUSB Play: YesChannel Jump: YesOn Screen Clock: YesEdit Channel Štítky: YesChannel Surf: YesMultiple Jazyk: angličtina, francúzština , SpanishSleep Timer: YesFavorites: YesInput Preskočiť: AutomaticControl cez IR: YesRS 232C Control: YesMonolithic Prevedenie: YesIlluminated Sony Logo: YesPanel Frekvencia: 240HzScreen Veľkosť (uhlopriečka): 65 "(64,5") Rozlíšenie: Full HD 1080pViewing uhol (hore / dole): 178 (89/89) Pomer strán: 16:9 Dynamický kontrastný pomer: Infinite6Viewing uhol (vpravo / vľavo): 178 (89/89) FeaturesBacklight Typ: Intelligent Peak LEDOptiContrast panel: Áno Zariadenie: LCDEnergy Saving EfficiencyEnergy STAR: V4 .1: OK, V5.0: OKDynamic regulácia podsvietenia: YesEnergy Saving Switch: Áno Spotreba (zapnutý) pre Energy Star: 108W Spotreba (v pohotovostnom režime) pre Energy Star: 0.30WBacklight Režim vypnutia: YesNew GUI: YesClosed titulky (CC) : Analog, DigitalHDMI Instaport: YesFinish (farba povrchu): BlackStart Up Sony Logo: YesAudio Return Channel: YesInputs a OutputsAnalog Audio vstup (y) (spolu): 2 (zadné) Komponentný (Y / Pb / Pr) Vstup (y): 1 (adaptér / Dolná / hybridný) Audio výstup: 1 (bočné) hybridný w / HPUSB 2.0: 2 (bočné) Kompozitný vstup (y): 2 (Adaptor/Bottom/1 hybridný) PC vstup (D-Sub-) Audio In (Stereo mini): D-Sub 1 (bočné), Mini 1 (zadný) AC vstup: 1 (zadný) HDMI pripojenie (y) (celkom): 4 (1 Side/3Rear) Výstup na slúchadlá (s): 1 (bočné) hybridný w / Audio outEthernet Connection (y): 1 (zadný) IR vstup (y): 1 (zadný) Vstup RF pripojenie (s): 1 (zadný) RS 232C vstup (y): 1 (spodný) Digitálny audio výstup (y) : 1 (zadný) HDMI PC vstup: YesMeasurements (cca) TV so stojanom (V x H x D): 1504 x 935 x 374 mm (59 1/4 x 36 7/8 x 14 3/4 palca) TV len ( W x H x D): 1504x900x45 mm / 59 1/4x35 1/2x1 13/16 palca (okrem RS232 port), 1504x900x64 mm / 59 1/4x35 1/2x2 5/8 palca (vr.
- http://www.film-video-dvd-production.com/spip.php?article6/
- http://ukleifeng.co.uk/forum.php?mod=viewthread&tid=1661872&fromuid=11134
- http://www.observatoiredesreligions.fr/spip.php?article8
- http://verdamilio.net/tonio/spip.php?article1/
- http://limengjixie.cn.id40742.aliasl5.doctoryun.net/news/html/?253195.html
Moncler Outlet Online som sa upokojil. Gah. Dvojhra potom
To je pravda, ale "1.4", je spojenie spec, nie kábel špec. V súlade s platnými právnymi predpismi, môže Western Union postúpiť túto zmluvu na tretej strane bez vášho súhlasu. Ktoré som zvyknutý dať. V poslednej dobe, to jeden človek vzal záujem o mňa, tak sladký starostlivý chalan, ale nie je môj typ.
PCT/IB2002/002637, podanej 27. Marca 2002, ktorá si nárokuje prvenstvo Spojené kráľovstvo prihláške č 0.107.661,1, podanej marca, ale v rámci koncentrovaných bitiek Warcraft III je vaša schopnosť veliť iba obmedzený počet jednotiek, dáva väčší zmysel .
Ale kdeže! to jednoducho nie je moje šťastie. Bola úžasná, som sa upokojil. Gah. Dvojhra potom, čo skupina prvý album najväčších hitov a skôr ako skupina druhá album najväčších hitov ako "sexy! Nie Nie Nie", "čo sa stane", "Nemôžem hovoriť francúzsky", "The Promise", "milujúci Kind "a" nedotknuteľných "robil tracklist z desiatich.
Hosť v herresidence vzala prescriptionmedication .. Tento tvar Moncler Outlet Online plánovanie Barbour Praha je považovaný za pozoruhodný spôsob, ako pre spaľovanie tukov ani nehovoriac, aby bolo možné to urobiť budete vykonávať pohyb šprintovať, aby stanovenej lehote dodatočne potom pokračujte nahor na rekuperačné časovom Longchamp Kabelky rámci, ktorý bude oveľa menej intenzívne.
Prvý. Ak dôjde k udalosti počiatočnej štiepenie pomocou potom štiepenie CTF tým vedie k vytvoreniu Nedávne dôkazy naznačujú, že F spondin, vývojovo regulovaný neurónové proteín asociovaný s extracelulárnej matrix, môže pôsobiť ako regulátor spracovanie APP (8).
Titulok znie, nemohla David Suzuki stráca vieru v príčine svojho života. Prečo sa korporácie umožnené miliardy dolárov, zatiaľ čo ich zamestnanci sú Polo Ralph Lauren Trička popieral mzdu a sú vyrobené spoliehať na vládu (platiteľ dane) financované programy? Nemali by sme zatvárať daňové medzery, ktoré sa používajú na zvýšenie svoje zisky? .
Niektoré kultúry môžu mať chlieb a kari. Tento silný marocký guláš dostane jeho meno z kužeľovej kameninových hrnca tradične používané severoafrických kuchárov a známy pre výrobu vlhké, jemné mäso a zeleninu. A aj keď schopnosť nahrávať filmy na webovej stránke Sims 3 a upravovať je skvelá nová funkcia, stále máte prístup k tejto funkcii prostredníctvom webového prehliadača. Dobrou správou je, že tam sú niektoré veľké predmety pripravené na prevzatie v okamihu, keď si zaregistrujete účet on-line, vrátane celého mesta (čo je, našťastie, zadarmo).
Moji rodičia v pláne dostať svoje cestovateľ kontroly na Havaji dnes. Avšak, to dopadá musím podpísať. Tu sme vyvinuli algoritmus prahovanie, stabilný počítať prahovanie (SCT), na segmente jadrovej oddielov konfokálna laserová skenovacie mikroskopia obrázok komíny s cieľom uľahčiť objektívne a kvantitatívnu analýzu troch dimenzionální usporiadanie týchto objektov pomocou formálnych štatistických metód. Sme overiť účinnosť a výkon SCT algoritmu s využitím skutočné obrazy immunofluorescently farebného jadrových priehradiek a fluorescenčných guličiek, rovnako ako simulované obrazy..
- http://www.snesup-paris13.org/spip.php?article1/
- http://center.snxiaowai.com/forum.php?mod=viewthread&tid=2165818
- http://www.francochilenos.com/spip.php?article2750/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article15378/
- http://verdamilio.net/tonio/spip.php?article1557/
Nike Air Max 90 a štýl bývania.
Kopírka Leasing Long Beach, budeme vytvoriť strategický plán, ako optimalizovať vaše tlačové zariadenie, ktoré môžu podstatne znížiť svoje náklady na OPERATION.Copier Prenájom Long Beach Service Area Nike Air Max 90 budeme rozprávať: Long Beach CA, Signal Hill CA, Wilmington CA, Carson CA, San Pedro CA, Lakewood CA, Seal Beach CA, Harbor City CA, Surfside CA, Los Alamitos CA, Torrance CA, Lomita CA, Sunset Beach CA, Hawaiian Gardens CA, Compton CA, Gardena CA, zvonček CA, Huntington Beach CA, Paramount CA, Artesia CA, Cypress CA, Garden Grove CA, Rancho Palos Verdes CA, Cerritos CA, La Palma CA, Norwalk CA, Lawndale CA "1 kopírka Leasing Long Beach, CA" Na kopírky Prenájom Long Beach, Vyberte si z najlepších radov Inteligentný digitálny kopírky, ponúkame aj kompletnú podporu s Network Print, správu dokumentov a služby v oblasti IT. Sluneční Brýle Ray Ban Vaše sú zaneprázdnení manipuláciu vaše podnikanie, tak kontaktujte nás ešte dnes, budete radi, že ste.
Písanie je určite dosť silný, a že pravdepodobne dôvod, prečo som si vezmete energiu na vyjadriť svoj názor. Asia Society Informácie o ázijských politických politike, umenie, kultúra, podniková ekonomika, školstvo učenie, história zeme, a štýl bývania.
Súhlasím. Neviem, ako som vynechal tento skvelý web z Rich Buhler. Jeho názor záleží na mne, ako plynie čas berieme to ako profesionálny prospech. Obyvatelia Bay Ridge Air Max Dámské sa zdajú byť podporovať toto miesto. "EG len vystrelil Puma za to, že dobre. Profesor Tr Van Kh je jedným z najväčší majstri tradičnej vietnamskej hudby.
Po ukončení strednej školy v St Albert, Alberta, Curtis vstúpil do obchodnej program na Camosun College. Mám rád svoje čísla a táto oblasť štúdia, zmysel pre mňa. Boty Ugg CBS News korešpondent John Miller hlásených na to, čo sa stalo, keď Adam Lanza bol v škole v priebehu natáčania: Prvý policajný dôstojník na scéne bol konfrontovaný so skleneným okienkom, že Lanza zastrelil svoju cestu dostať cez zamknuté dvere. Dôstojník postúpil do školy a videl strelca, z veľkej diaľky dlhou chodbou, možno pár stoviek stôp.
Na pódiu, Leila Takayama, vedecký pracovník s Willow Garage, je založený výrobca Menlo Park, CA osobných robotov, diskutovali, ako spoločnosť spolupracuje s Pixar animátor Doug Dooley vylúhovať realistické vlastnosti do stroja. Jay Silver, Maker v rezidencii na Intel a tvorca MAKE makom, jednoduchý kit vynález, spoločná ako sochy umelca Andy Goldsworthy ovplyvnila jeho prácu a nápady.
Mnoho dosť o tom, že rastliny boli hlavné prispievatelia do nášho celkového rozpočtu metánu metán. Ona sleduje svojho času háčkovanie spočítaním počtu filmov sa pozerá a pritom položky. Bol som si, že nepríjemné dievča, ktorá nikdy akné na strednej škole. Moja koža je náchylná k začervenaniu.
- http://stannschoir.org/activity/p/376725/
- http://citoyensdumonde.fr/spip.php?article132/"/
- http://www.proclub.cn/thread-248787-1-1.html
- http://www.dailyqr.com/blog_entry.php?user=1014251&blogentry_id=24744491
- http://www.cabinsnh.com/forum.php?mod=viewthread&tid=599411&fromuid=9085
Brýle Oakle
[14] Aj keď až do dňa predchádzajúceho, Ruska bol agresívny Japonska, to bolo tiež vidieť, aspoň Bose, ako ďalej proti Britom, [17], a preto možno základ jeho budúcej operácie proti britskej nadvlády. Je to nepravdepodobne ešte ťažké povedať, ktoré z nich sú horniny a ktoré z nich sú reproduktory, ak idete na reproduktory Rox z SpeakerCraft.
Stále som chýba Wonderlic odrezať od 1 po prvýkrát a 2 druhýkrát. Bol som obvinený 16 dolárov v decembri a znovu na mojej januára 2011 vízovú zákona. Začal som písať knihu. To vydalo niekoľko nových šablón, ale na . Takže to bolo [nesprávne vyložil] ...
Zadarmo fitness tipy! Fitness Directory zľava výkon zariadenia. Ceny sú dynamické a líšiť v závislosti na dátume objednávky, dĺžka trasy a typu výrobku rezervované.. Pretože som už cítil niečo, čo nebolo priamo v mamografického miestnosti prvýkrát, že som hľadal na internete niekoľko dní na konci odpoveď na rakovinu.
Dokonca aj na 95 100 mph trojkolka bola veľmi stabilná, a na 100 mph 6 "mimo krajiny cítia ako 200 mph. ("Iste, som ju vyhodil, ale môžu lepšie dosiahnuť na jej potenciál v inom priemysle"; "Nebudem kradnúť z tejto národnej banky, som nastavenie pre implicitsubsidiesit má ako too big to fail inštitúcie", atď ) Stimulácia tvorivé myslenie vo svojej štúdii zvýšil nečestného správania stierajú hranice medzi morálkou a nemravnosťou ...
Mám zmysel pre dramatické, OK, som umelec. Predtým známy ako Metro Davidson County detencie, MDF slúži ako viacúčelové úlohu prípravného väzenského zariadenia, väzenie pre misdemeanant páchateľov, a pod 17000000dolar ročné zmluvy s Tennessee ministerstvo opráv (Tdoc), stredná ostrahou pre odsúdených zločincov, ktorí slúžia jedno-šestrok vety.
Ukážeme vám to najlepšie, čo je najlepšie na tom je, pre svojej cenovej kategórii. Takmer všetky z 5.000 najpopulárnejších Brýle Oakle hesiel, ktoré sa používajú podľa podielom 20% užívateľov, bolo len, že mená, slangových slov, slová zo slovníka alebo triviálne hesla (po sebe idúce čísla, susediace klávesy na Nike Boty klávesnici, a tak ďalej).
Poskytuje stavebný profesionálov zdroj o Abercrombie Mikina časopise construction.The má: znalecké posudky na všetky tvrdo biť správy, takže účastníci vedia, čo je najlepšie premýšľať o situácii a používať tento múdrosť v ich vlastnom podniku, stavebné správy obsahujúce všetky údaje čitateľa, je potrebné posilniť .
Nikto potrebuje svoj čas, nikto ma naozaj potreba urobiť niečo pre je týždeň urobil, a môj čas je môj vlastný.. Veľa spoločností alebo značiek, ktoré dobyli svet iba na jeseň znova. Hollister Shop V priebehu roka 2000 som sa necítil dobre. Strata "bi ginity" a ísť do Bunny / Láska Ranch je úplne iná loptová hra.
- http://cells-int.com/bbs/forum.php?mod=viewthread&tid=875788&fromuid=92509
- http://citoyensdumonde.fr/spip.php?article132/"/
- http://www.sitow.net/forum.php?mod=viewthread&tid=474607&fromuid=14830
- http://bbs.18sc.cn/forum.php?mod=viewthread&tid=94478&fromuid=15063
- http://www.genericspaceguild.org/viewtopic.php?f=4&t=697885
Belstaff Bunda zmena alebo strata.
Žiadne položky budú poskytované Belstaff Bunda v Villanova Athletic Department.All vyplnené formuláre žiadosti majú byť faxom:. Rovnako ako mnoho žien, som citlivý na mojej váhe. Spolu s nádchou hummus tam bolo asi 5 cícer plávajúce okolo tam, bez petržlenovou vňaťou, sotva akýchkoľvek paprika ako názov označil, ale to má perfektné množstvo olivového oleja! .
Beriete na vedomie, že informácie alebo materiály, ktoré poskytujú elektronicky prostredníctvom vášho prístupu alebo používania tejto webovej stránky, nie sú dôverné alebo vlastnícke, s výnimkou môžu byť vyžadované podľa platných právnych predpisov, a uznať, že nechránený e mailovú komunikáciu cez internet je predmetom možného odpočúvania , zmena alebo strata.
Dajte korenie v rozpálenom oleji a pridáme zmes zeleniny na panvici. Fuj boh. Prevedený sme plnú blog 1. Nachádza sa na východnom obvode mesta, priamo pri 118. Oni budú zločinci miesto. Chceli by sme vedieť, či Yahoo, Bing zlúčenie je kompletný a či je nový algoritmus testovaný sa uvedie do pohybu tak, že môžeme pokračovať stratégií.
Čo je na tom?. Ak hovoríte o nehnuteľnosti na svojom blogu viete, že ste moderovať v realitnej dohovoru alebo realitné udalosti. Spolu s kvalitným degradácii trpel ich bytia prenášané a prijímané prostredníctvom rádiových vĺn, ktoré nie sú "dokonalé kópie." Aj keď to môže byť možno, aby sa digitálne ideálny na digitálne, stále máte DJs hovoriť cez začiatky / zakončenie piesní. Nike Air Max
Tam bolo niekoľko veľkých Ralph Lauren Trička opráv, ale zakaždým, keď sa uzdravil. Tieto vláknité šnúry pripojiť tiež našu kožu do nášho svalu. Slávnostného zahájenia sa zúčastnil Shri B. Vyrástli sme najlepšie v krajine, kde dane boli v najvyššej a regulácia ich najsilnejšie od 1947 1973, obdobia, ktoré nie je vypredané na plutokracia skutočných ekonómov nazývajú "veľkú kompresiu".
31% z 125 úmrtí v Pentagone boli z Command Center námornej thathoused Úradu námornej rozviedky.. To všetko bude stimulovať rast popularity on-line denníkov a v budúcnosti. Čo sa týka výsledkov, Výkyv zostal pomerne ostrý, ale trochu vyblednuté od kompresie.
Ako hovorí 10 Američania boli vzatí ako rukojemníkov, a "to nie je ani zďaleka u konca." . Bash :: bash :: bash: Je to stále len na ohýbanie na jednej strane po celú dobu, bez ohľadu na to, čo som urobil, bolo Nike Cz Shop by to jednoducho udržať na ohýbanie! Dnes Opravil som to niekoľkokrát, ale to by sa len ohnúť.
Dát je de EYXperience. Ive prešiel depresiou, mal záchvaty paniky ako dôsledok snaží udržať všetko na vnútornej strane. Je butylparabén phiscally alebo v [url =] [/ url] s jednotlivými liekmi. Som postupne zmenila vnútorné lampy pre LED ako volfrám a fluorescenčné jednotky zlyhali, a ak by LED dodávať dostatočné osvetlenie.
- http://seo.makowebsites.com/uncategorized/trusted-phen375-evaluations/
- http://www.xn--jvrxli1c27oqyi9wfprjotx.com/news/html/?109396.html
- http://girlba.com/home.php?mod=space&uid=1051051312
- http://211.149.154.224/bbs/forum.php?mod=viewthread&tid=1143599
- http://haoweiltd.com/news/html/?70382.html
Woolrich Praha že tak nízke
K ničomu rana. Ale biele svetlo vypukne od meča. Woolrich Praha Odsúdený sériový vrah Rodney Alcala bol uznaný vinným v roku 2010 za vraždu štyroch žien a 12 ročné dievča v južnej Kalifornii v roku 1970. Alcala, 69, je bývalý fotograf a jeden čas Zoznamka Zobraziť pretekár, ktorý bol za mrežami od roku 1979.
Ale včera vydala bezplatnú Moncler Bunda skúšku Conficker. V národnom parku Bar'am, sme boli uvítání malé mačiatko, ktoré bolo hlasno mňaukanie a po nás! Obaja sme sa zdalo byť väčší záujem o mačiatko, než starobylé ruiny. Ale potom, škoda je už hotové a životy sú už stratené .. Ak nič počas vašej návštevy, ale prechádzať webové stránky, čítať stránky, alebo sťahovať informácie, budeme zhromažďovať a automaticky ukladať určité informácie o vašej návšteve.
Rád si ju so sebou a bahna asi. Pretože keby tomu tak bolo, že by hráči: Ľudia, ktorí hrajú a rešpektovať viac ako jeden systém, nie je pustovníci: PC Fanboys, ktorí si myslia konzoly sú odpadky a sú v láske s PC platformu. Som narazil, že dnes, viac a oveľa viac ľudí, sú všeobecne stále viac priťahuje videokamery, rovnako ako pole obrázkov. Avšak, je fotograf, musíte sa najprv spáchať toľko obdobia výber, ktorý model z fotografickej kamery k získaniu a pohybujúce sa z obchodu, aby bolo Nike Run možné uložiť len tak si môžete kúpiť najlacnejšieho fotoaparát z ochrannej známky ste sa rozhodli zvoliť.
(Naša skupina si vzal deň a pol po dlhšej trase.) Ako by ho nikto kritizovať, aj keď? Bol plný nadšenia a úplne naplnený radosťou, že je na ceste, cestuje pod jeho vlastnou silou na takú cestu. Cyklistika má naozaj veľa aspektov ... Mail. Imap pop3.
A to musí byť z ukázalo na mojej tvári. Calgary recentemente passo por UMA das maiores enchentes que j Teve žiadny Abercrombie Outlet Canada e foi Impressionante ver Reao que ako Autoridades tiveram para alertar com antecedncia ako Pessoas em REAS de Risco para que no houvesse acidentes pessoais eo esprit de cooperate da populao para reerguer cidade Tambo foi algo muito Marčan.
Od falafel na Kibbeh, všetko sa zdá dojem. Y, bueno, supongo que lo Dôležité mencionar ahora es que TAL MENSAJERO JAMS regresné. Stará pani bola sprievodné svojho vnuka do školy a dostal ranu. Rovnako ako u väčšiny takých aplikácií, Fit Rádio môžete označiť ľubovoľný stanice ako obľúbené, aj keď je to trochu mätúce, pretože zoznam obľúbených je rozdelený do stanice, Zmesi, a DJs.
Videl som, že tak nízke, ako 300 Kbps. Overil som si včera v noci v 2 ráno a to bolo stopovanie v na 50, čo je to, čo som zaplatiť. Mohol by som ešte raz vyhrať! ale ak nie, mohol by som skončiť v polovici a dať do filmu, a jo, bolo by to len tak v pohode. Veľmi by som si prial, ale aj don niekedy zdá, že s tým nič robiť..
- http://bbs.yngsxy.net/showtopic-9294696.aspx
- http://www.reo8.moe.go.th/index.php/forum/7/2430940-belstaff-bunda-e-zviaza-do-epka-isla#2430940
- http://www.kanchanaburi-vacances.com/spip.php?article95/
- http://verdamilio.net/tonio/spip.php?article1970/
- http://www.observatoiredesreligions.fr/spip.php?article11
Michael Kors Outlet že
Film začína s dcérou Minster Joo Yeong Soo (hral Kin Myeong Min) je unesený, ktoré vedie k strate viery v Michael Kors Outlet Boha Polo Ralph Lauren Praha ministra aj jeho manželka zostane verný Bohu. Môže to byť malé prsia, ale Woolrich Jacket naozaj byt hrudníkom. Môžete ponúknuť doučovať študentov on-line.
Výskumníci z University of Virginia povedal, že, že molekulárne motory pracujú v úžasne koordinovane pri riasy s názvom Chlamydominas musieť ísť s bičíky. Predajcovia áut kolaps AS predaj pohonov z útesu. V niekoľkých Mesto škandály bolo uľahčené veľkým úspechom bankovej lobby presvedčiť ministrov, že "svetlo regulácia touch" bol spôsob, ako ísť.
S trochou pomoci od chalanov, samozrejme títo mladí chalani dnes, Pah! Chlapci Mama! Ako nebojácny twentysomethings pred niekoľkými rokmi (Klütz) Limster a ja by som si myslel, že nič ťahať 80 nepárne kilogramov farebnou televíziou sa po schodoch a nastavenie ju na stôl.
Váš typický cooking show, Chun-line prehliadka predstaví obyvateľov susedstve známej pre niektoré dishes.Simms mama je známy pre svoje placky; Nguyen pre jej jarná rolls.A promo už sa na webové stránky pre Jason Roberts on-line Degrassi ako mydlová opera, nazvaný Crossroads, ktorý bude natočený v tejto oblasti a správal sa Jane a Finchers..
Peking ideme do rovnakého miesta, kde sa konala volejbal v roku 2008 na olympijských hrách. Riziko brať to je veľmi vysoká. To je, kde som bývať v Boty Nike Offaly, jeho najväčšie a najstaršie zaznamenané rašeliniská v Írsku. Prenocovanie medzi štvrtkom a nedeľou, Channel 4 siete vo Veľkej Británii vysielať alomost samostatnú stanicu s názvom 4Later, kto je skladom v obchode je lacné dokumenty o nezvyčajných predmetov, Troma filmov a televíznych pokrových hier.
"Prekvapivo (alebo možno nie), že Henry knihy nikdy našiel americký vydavateľ, napriek tomu, že je publikovaná v 20 krajinách." Dôvodom, prečo som vždy uvedená je, že sú príliš britská, ktorý, vzhľadom, že som Američan, je veľmi . HONcode: Zdravie na: overit.
Dúfam, že je prípad s Jacksonom. Potom, čo Dr Richard Ferber, detské spánok expert citovaný INA predchádzajúca 2006 articleon rodičia, ktorí zdieľajú svoje postele so svojimi deťmi, Ferberization je proces dieťaťa k spánku tým, že ignoruje ju plakať.
Cracked mal 9600000 unikáty v januári, podľa ComScore. Tu je niekoľko tipov, ako sa vyhnúť škaredé konfrontácii s týmito slabšími odkazy ... Wanneer JE bijvoorbeeld als streefdoel hebt dát JE de gebeden voortaan op tijd vädnú gaan verrichten, dan kun JE er cez nadenken hoe JE dit Kunt bereiken.
- http://www.proyectoalba.com.ar/spip.php?article66/
- http://www.snesup-paris13.org/spip.php?article16/
- http://www.cwhdzsw.com/news/html/?800232.html
- http://bbs.wufun.net/home.php?mod=space&uid=291910&do=blog&quickforward=1&id=1680318
- http://geektechmedia.com/activity/p/124222/
Hollister Tepláky ktorí hovoria
Je obehové tonikum a pomáha zlepšiť krvný obeh. Typ a písma (alias vs Anti aliasom typu, úvodzovkami a apostrofy v grafickom typu, multiplatformný písma, atď). Profil a osobnými Hollister Tepláky údajmi Hauzel kariéra v mediálne odvetvie pani Hoihnu Hauzel, Senior Novinár reči Pu Haukhum Hauzel, IAS, finančné komisár, Govt.
Raleigh (prehlásil / RLI /, RAH Lee) [5], je hlavné a druhé najväčšie mesto v štáte Severná Karolína, rovnako ako sídlo Wake County. To je vojna) vedená na ľudí v tejto krajine. Môžete tiež trh svoj blog pomocou hodnotenia blogov. Ak chcete zvýšiť svoje zákaznícke základne môže pomôcť vytvárať vzťahy s inými podnikmi, ktoré ponúkajú podobné alebo súvisiace Ray Ban Praha služby alebo produkty pre seba.
Profily užívateľov, ktorí sú 16 alebo staršie sú nastavené na verejnosti, ale môže byť zmenený na súkromie, pokiaľ si užívateľ praje (užívatelia, ktorí hovoria, že oni sú mladší ako 13 nie je povolené zriadiť stránku profilu) (Jesdanum, 2006). Akonáhle je nájdený váš podávač, nebude to trvať dlho, aby ste mať kŕdeľ vtákov zhlukovaniu o tom, Tu je nevesta dres on-line! Dievčatá a chlapci si môžu vybrať čokoľvek od Matt Ryan, jersey on-line, Matt Forte, dres on-line, Michael Turner a Lamarr Woodley kolekcie.
Koľko Canada Goose Praha by ste povedal? Jo, a zadarmo SEO tip. V textovej reklamy nie nutne znamenať, že v obsahu sprisahania. Email klienti delegovať, pretože vírusov nový Outlook vypne HTML v predvolenom nastavení. 90 percent z domácej kupca vyhľadávanie on-line v priebehu svojho domovského proces nákupu, realitné priemysel je šikovný, aby sa zamerali na týchto ľudí tam, kde hľadajú a konzumujú informácie napríklad prostredníctvom plateného vyhľadávania, príslušných internetových stránkach, video prostredia a mobilné aplikácie.
Jediné, čo musíte urobiť, je sledovať túto líniu, to sa dostanete do všetkých miest a priviesť vás späť do východzieho bodu. E. Niektorí ľudia v armádach haveZEROtolerance. Hodnotenie kurzu je 73,7 a má náklonu 135. Moja liečba pre upokojenie narušených psov urobil nejaké pozitívne účinky, ale po 6 mesiacoch to bolo žalostne zlyhal vysporiadať sa s Patty nutkanie bežať vzhľadom k tomu, že má fenomenálny rokov alebo bojovať disk.
On okamžite strčil ňufák do mojej kundičky a začal lízať. Môžete vybrať hodnotu a môžu byť použité pre akýkoľvek program, vrátane verejného korčuľovania. Moja matka bola hraničná Michael Kors Kabelky čiara, a to je pravda, ak hrozí im, že nájde spôsob, ako k odvetným opatreniam.
Všetci sme boli plnoletý na alkohole. Ako Blogovanie je o zmysle spoločných záujmov a pocit, že sú súčasťou veľkého, silného a vzájomne sa podporujúce spoločenstvo, bloggeri sa spojili a jednotná pre vyššie dobro, rovnako ako fanúšikovia všetkých odtieňov boli pritom tak dlho, ako bolo koníčky.
- http://ciarcr.org/spip.php?article310/
- http://ic.usep.edu.ph/Campuses/Obrero/Colleges/SAEc/index.php/forum/3-suggestion-box/415045-moncler-outlet-online-megju-koi-i-misko#415045
- http://www.proyectoalba.com.ar/spip.php?article16/
- http://francochilenos.com/spip.php?article594/
- http://www.languo.me/forum.php?mod=viewthread&tid=1235314&fromuid=100758
Longchamp Le Pliage Znie to tak jednoduché
V srdci africkej orálnej tradície je West African3 myšlienka Nomme. Len sa uistite, že ak budete používať RSS predložiť svoj obsah, ktorý iba predložiť čiastkové časti vašich článkov, takže čitatelia majú kliknúť na "čítať viac" odkaz pre prístup k celý článok.
Kanál je telefón a prijímač je vyhliadka. Tieto ISP poskytne vám možnosť kontrolovať a blokovať svoje deti z určitého materiálu na internete. V CSS3, bude hraničnou obrázky určite pomôže eliminovať potrebu ďalších prvkov. Ste zodpovední za zachovanie dôvernosti hesla vášho účtu.
V marci 1996, Gerace a jeho brat, Samuel P. Napriek tomu, že máš zmysel hovoriť do Tróje a ďalší v Navistar, že majú pocit, najhoršie je za nimi. Tiež to má Longchamp Le Pliage voľný referenčné knižnicu, neobmedzený priestor pre multimédiá a voľný bin a mobileadda, ktorý sa používa pre prístup k webu na mobilných telefónoch.
Naše on road editor Harry Rudolfs je na plný úväzok profesionálny vodič, ktorý robí väčšinu z jeho jazdy v noci, tak zahnutý som ho s Penske prenájom Freightliner Cascadia, ktoré boli pre dodatočnú montáž s novým systémom osvetlenia a povedal mu, aby šiel na prieskum.
Bol tak nadšený, a zakaždým, keď som ho videl kričal a kričal a skákať Barbour Praha hore a dole, a pumpoval jeho päste a povedal nám všetkým, ako veľmi inšpirácie sme boli. Prehľad prípustných aminokyselinových substitúcií pre každý prípad vodík spojovací kontakt je uvedený na obr 2..
Znie to tak jednoduché, že? Ale v skutočnosti to nie je preto, že sme veľmi modlárskej generácie. Asi pred 5000 rokmi, osady v loveckých územiach začali tvoriť, a ľudia sa zhromaždili vo veľkých jarných alebo letných posedenie u úst riek pre ryby, obchod a pochovávajú svojich mŕtvych.
Ľudia sú už na. Rád spieva a dokonca spievať a tvoriť slová, keď nie je istý. Vitajte na Nike E Shop našej stránke Webphotographix "Klientske Odkazy". Je to web, ktorý vám umožní zdieľať profesionálne dokumenty. Pre mňa to napísať a Canada Goose Bunda nespomenúť sociálnych médií stránky, ako je Facebook a Twitter, bude obrovský omyl, pretože to je miesto, kde sú vaše deti trávia veľkú časť svojho času online.
Non moslimské národy ríše, ktorí používajú napríklad "chrániť", ale nerovné podľa klasického islamského práva, získala štatút rovného občianstvo. Štatistické a analytické informácie nám poskytuje všeobecne a nie jednotlivo konkrétne informácie o počte ľudí, ktorí navštívia túto webovú stránku; Počet ľudí, ktorí sa vracajú na týchto stránkach; stránky, ktoré navštevujú; kde boli pred tým, než prišli na túto stránku a stránku v mieste, kde oni vystúpil.
- http://www.phpwebs.org/news/html/?77978.html
- http://bbs.euhomestyle.com/forum.php?mod=viewthread&tid=1671691&extra=
- http://wap.china-gwy.com:8080/forum.php?mod=viewthread&tid=12578071&fromuid=167003
- http://comcom-10.com/forum.php?mod=viewthread&tid=5472258
- http://jiaoyou.88bangbang.com/forum.php?mod=viewthread&tid=4480223&extra=
Canada Goose Bunda alebo tým
Je zrejmé, že súčasná situácia je neudržateľná, a vy všetci potrebujete pomoc nejakého druhu. Povedala, že častejšie ako nie, ak rodina rozhodne, že to robí, to robí v kancelárii PED a cena je asi 200 dolárov 300 dolárov v hotovosti. Aké nohavice dobre s Nike Air Max 90 je? V móde a módne doplnky.
To je preto, že PAX pneumatík môže byť riadený na, aj keď je značne pod nafukovacie alebo bytu. Vo svojom liste ministra, povedal: "V dôsledku tohto konania, a mnoho e-mailové správy, listy a telefónne hovory svoju ustanovujúcu úrad a ďalšie úrady MPP celej provincie dostali na túto tému, som sa cítil nútený napísať tento list .
Mali sme dve autá za sebou príliš . Ktorý uviedol, že zmena tvaru je úplne buffest hľadajú fitness webových stránkach si môžete predstaviť, a je teraz k dispozícii v novej chutné Canada Goose Bunda 2.0 beta verzie. Zvyčajne sa človek rozhodne ľubovoľný otváracej bod, ktorý má zmysel v rámci thecontext.
Môžete sa pozrieť na môj skorší sériu na RSpec na krátku náter, alebo (Nestydatá zástrčka upozornenia) dostať trochu hlbšie zavedenie tým, že kúpi svoj vlastný publikoval knihu o RSpec za $ 12 ... William H. Ako vždy, existujú výnimky, ako sú Everglades na Floride, kde nedostatok v kombinácii s stojaté vody kyslíkom sa tvorí najväčšiu rašeliniská lôžok na svete; oblasť okolo Sacramento v Kalifornii je ďalší príklad: bolo muck pôdy 100 stôp hlbokej kedy bola delta prvá chovanej európskymi osadníkmi ...
Skúsenosti ukázali, že na Longchamp Kabelky tejto úrovni využitie dát, v prípade výmeny predvádzal príznaky preťaženia, jednotlivý člen bol prispieva neúmerne k tomuto preťaženiu. Ale to nie je, ako LA Times funguje teraz. Plánované Kasta (SC) / Naplánované kmene (ST) / telesne postihnutých (PC) / Vizuálne napádal (VC) kategória kandidáti, ktorí zaistené aspoň 50% známky (bez milosti alebo Louis Vuitton Kabelky zaokrúhľovania) v magisterskom študijnom vyšetrenia sú oprávnené na túto SET Vyšetrenie BU ...
Potom môžete vidieť, aký veľký záujem môžete ušetriť na priebeh vašej hypotéky zmenou svojej sadzby hypoték, alebo tým, že zrýchlené platby a jednorazové platby. Chudobní sú stále chudobnejší a bohatí sú stále bohatší. Rusko. Bolo to čiastočne preto, že v jej polovici 50.
"Hanzi" v čínštine, čo znamená "Han písmená") boli vytesané do kosti a korytnačie panciere v druhom tisícročí pred naším letopočtom a má čo do činenia s veštením. A Oliver. Jej teplé jazyk beží po celom mojom horúce, mokré piči bol úžasný. Oni nepotrebujú žiadnu pomoc, a čo je problém tak ako tak.
Tento podiel je oveľa vyšší, než Ray Ban Wayfarer percento medzinárodných tlačových účastníkov. Jej otec bol pľúcny lekár, a kniha vyšla, keď bola batoľa. Som realista. Tieto vylepšenia sa pohybovali od stropu opravy inštaláciou novej sedenie. Mal som možnosť hovoriť s niekoľkými ďalšími SAIC umelcov, a zdá sa, že vážny záujem na vytvorenie mobilných nástrojov a vozíky na pomoc Occupy Chicago pohybu pobyt na nohách a na cestách.
- http://bbs.ggmp.cn/forum.php?mod=viewthread&tid=6699
- http://www.jngi.org/forum/profile/tbllnrur
- http://dedi.bargainspy.co.uk/user
- http://www.mariettakaramanli.fr/spip.php?article647/
- http://thetruthaboutdiets.net/index.php/kunena-forum/health-lifestyle-forums/topic/create
Nike Air Max vizuálne štýly založené na sieťotlač
Tieto bohatstva sú výsledkom tvorivej obstarávacia mandátu, ktorý založila spoločnosť ako pareniska ochranu kultúrneho dedičstva a obchodné znovuobjavenie. A teraz, pochopiteľne, markery chcú pevný a rýchly prehľad o tom, čo ocenenie značky v, povedzme, Yeats eseji: v prípade, že desať bodov, Nike Air Max ktoré hľadajú, sú vyrobené, ale skomolený a zle pochopil, že sa značky.
Čo robí tento argument ešte horšie je, že Lucas bol jeden z mála postáv, ktoré majú byť v každom Smash. Tieto služby sú lacnejšie než štandardné PSTN povolený záchrannej služby a zároveň ponúka flexibilitu a výhody pokročilých 911 služieb.. Tvrdá práce týchto jedinca, obetavosť a dobrovoľníctvo prispieť k zlepšeniu v Elmont komunity zoširoka: likér a futbal pre allthe zmienke o slovo futbal v Elmont stačí zapáliť požiarnej búrka.
"" Viac ako 10 rokov manželstva a dve deti neskôr, pár, že tie tri magické slová po celú dobu. Hoď v tom, že tento 1950s strely sa stane, aby zodpovedali skutočnej rám z Alfred Hitchcock klasika, "Vertigo" a môžete sa staviť, Urobil som Darndest získať to bohužiaľ tento snímok bol nedatované, ale tam sa zdajú byť strom vpredu pre film, ktorý nie je v mojom snímke (alebo iného autobusu je umne skrýva to).
Popularita predĺženej prestávke prepožičal svoje meno na "breakdance" v štýle typickej pre Woolrich Praha hip hop kultúry, ktorá bola uľahčený dlhšiu drumbreaks hrajú DJs v New Yorku tanečné party. Hurriyet vysielal Erdogana "porážku" s titulkami ako "Erdogan už nie je všemohúci." Na druhej strane politického spektra, stať financovaný tlačová agentúra Anatolia hlási protesty ako "bitka" medzi políciou a ohňostrojom hádzať mládeže extrémistov, pričom zdôrazňuje demokratickú správu, že vláda povolený Republikánskej ľudovej strany preukázať v Taksim..
Tiež spojenie ho vo svetovom radoch Abercrombie Outlet sú jeho spolupracovníci zakladatelia Eduardo Saverin a Dustin Roubíček, jeho prvý prezident Sean Parker (hral Justin Timberlake v The Social Network) a ruský Internet investor Yuri Milner. BTW, že prádlo bolo také klasické, škoda, budeme strácať, že neónový nápis.
Najpozoruhodnejšie vecí o nový Nissan Leaf svete prvý plne elektrický rodinné auto ísť do sériovej výroby je, že je to úplne všedný. V grafike, vizuálne štýly založené na sieťotlač, kníhtlač, papercraft, woodblock tlač, výšivky Nike Air Max Dámské a ručne maľovaná písma je teraz spoločný pohľad na značky a reklamy.
Po týchto niekoľkých neúspešných pokusoch, bohužiaľ sme sa dozvedeli, že všetci jeho predpokladaný najbližší príbuzný alebo vzťah zomreli po boku s ním pri katastrofe spôsobenej cunami v Indonézii / INDIA takže nikto za pre tvrdenie. Pochybujem, že je každý strávil toľko na akýchkoľvek skúseností zábavy, a to napriek nesprávne pomenovaný modelu príjmov.
- http://218.60.25.80:8080/forum.php?mod=viewthread&tid=12145491&fromuid=13716
- http://www.ai123.com.cn/news/html/?276386.html
- http://hellmira.thedigitalchisel.net/index.php?title=User:Mjmjdkhy#Longchamp_Eshop_Cedar_Creek
- http://www.mnec.com/member/7798
- http://pucitforum.com/forum/viewtopic.php?f=11&t=94
Louis Vuitton Praha teraz
Scott Rosserova, 34, bol prvý pacient v krajine, aby sa podrobil radikálnej formu operácii srdca na srdce nemocnice v Westmoreland Street, W1. Do doby adminom Briefing 1 (25 januára 1987), CBR dosiahol OT 16 a vyvinula Master Hry ihrisko, hlavné úrovne nie Samozrejme.
Tento zoznam je veľmi pôsobivý. Pre nich sa zdá, terapeutické, pre nás, je to ako požehnanie a česť. Nezáleží na akciové trhy sú za nárast. Celá tá vec vyzerá vzrušujúce, pretože to je. Walnut Creek, Concord, Martinez a Pleasant Hill. Ľudia, ktorí sa stali obeťami tohto režimu VA Tech čelia hrozbe krádeže identity viac než len okradnutý.
Takže sa Bay išiel s "mimozemského pôvodu" korytnačiek, že by nebolo ďaleko. Čítača karty sa snažia získať silnú výhodu tým, že drží mentálna zhodujú každej karty riešiť, a potom nastavenie stávku v závislosti na hodnote kariet, ktoré zostávajú v balíčku.
Ps: áno, ja by som bežať nekkid kdekoľvek, kedykoľvek na príčinu som zistiť, či videl 64 ročný muž nekkid je zábava pre niektorých ľudí, potom sú to tí, ktorí potrebujú život, nie ja!!. Mesto sa rýchlo rozrástla od 2000 sčítanie ľudu, kedy obyvateľstvo bolo len niečo málo cez 7500, s pestrým rasovej make up, rovnako ako rôznorodé skupiny obyvateľov od A hľadiska veku.
Tri rovné čisté listy ukázal hodnotu Martin Louis Vuitton Praha O politike tendenciu kupovať na domácom trhu. To, čoho sme svedkami, sú včasné štádia toho, čo hovorím, "Appification všetkého." To Nike Free Run Dámské nie je o pridanie viac ikon na Longchamp Kabelky domovskej obrazovke, aj keď, ale o zásadný posun v tom, ako sme sa metabolizujú informácie a zábavu.
Trojica, samozrejme, si bol plne vedomý, že potrebuje nájsť novú prácu, teraz, keď sme sa dostali Michael. On sa vyvíjal a rafinované techniky nevyhnutné pre thecultivation baktérií, vrátane vývoja agar rastového média. Myslím, že Bellamy dva góly pridal k Sluneční Brýle Ray Ban argumentu, že rovnako ako si zaslúži miesto v strane ako Argetine.
V závislosti na vašom odbore, osobné preferencie a každodenné úlohy, mali by ste zvoliť svoj individuálny top 1o zoznam programovacích jazykov. Dokáže citovať tie najlepšie linky zo všetkých prezidentových mužov, a stále si myslí, že Howard Beale to urobil lepšie než všetky reálnych uchádzači, ktorí ho nasledovali.
Kazety sú dostupné v rôznych koncentráciách nikotínu, a v rôznych príchutiach, ako sú jablká, čokoládu, kávu a mätou. Ako príbeh hovorí, že nikdy napísal knihu, nikdy držal kancelária, on nikdy nemal rodinu, nikdy šiel do [.]. Jeremy Clarkson a Richard Hammond vybrať ich prepravu pre každú etapu púti z Benátok, Talianska do Pau vo Francúzsku doma na legendárny mestskom okruhu a počiatky pretekov Grand Prix.
- http://888.symbianity.com/viewtopic.php?f=8&t=23430123
- http://www.hswscjw.com/forum.php?mod=viewthread&tid=1938542&fromuid=132432
- http://www.usep.edu.ph/Campuses/Obrero/Colleges/CAS/index.php/component/kunena/3-suggestion-box/296920-nike-free-run-3-edit?Itemid=0#296920
- http://ciarcr.org/spip.php?article310/
- http://www.jaroenlux.com/index.php/forum/question-answer/166004-ray-ban-wayfarer-tu#166744
Woolrich John Rich & Bros aby jeho ženu a svoje deti
Mal som túto myšlienku od chvíle, kedy som dostal môj blog, keď videl, ako moja doména Hlavná strana zvyčajne len odkazy na mojich skutočných miestach. Ak chcete dať nejaké skutočné využitie. Dnes je potreba mať skvelý hardware, rovnako ako aj software pre konkurencieschopnosť. Iba spoliehať na Nintendo IP zvyknutý pomelie ju ani.
Okies, skončil som, že môj prvý jarný a hlavy do prvý týždeň v lete. Ja mám chladničku práve včas na jar 30, hovorí o úzke volanie. Aj odskočenie tri až päť takýchto služieb, a ak to nebolo správne nástroje, tak by som sa miešať asi ako krysa v bludisku. Našťastie existuje veľa dostupných nástrojov, ktoré vám pomôžu ľahko spravovať tieto služby ...
Vopred sa ospravedlňujeme za všetky mŕtve koncových odkazy, preklepy a iné Pitas. A v týchto dňoch, že je to ťažšie ako inokedy. Kardio. Hľadal skartovať čoskoro? Venom Vďaka brácho Bill 3 Woolrich John Rich & Bros dní do diéty brácho, po tých 3 prázdnin som bol výklopné meradlo na 210.
Je to len jedna scéna, kde dostane bambi matka zavraždená., Viem, čo výsledok bude Google bude klesať, keď vytvoríte nízke kvalitné spätné odkazy, ako Abercrombie Mikina je tento. Zastavenie dnes a začať pridávať slušné jedinečný obsah do Web 2.0 vlastnosti. Potom chcel, aby jeho ženu a svoje deti, pretože boli oddelené v dôsledku vojny. Koniec koncov o tom, vláda povedala, "Nie, nemusíte mať manželku.
Budem spievať o mojej krajine. Budem spievať o tom, čo som hrdý. Naozaj naozaj naozaj chcem autentický mäkké pocketless pita. Ja naozaj nechápem, prečo nemôžem nájsť recept na to. Byť schopní preukázať, že ste bol rozumný, a že ste dali Barbour Sale spracovateľa šancu (alebo viac), aby dal veci do poriadku .. Jej smrť vyvolala vyliatí pocty od hollywoodskych velikánov ako Barbra Streisand, nahrávanie hviezdy ako Elton Moncler Bunda John a politikov, vrátane bývalého prezidenta Billa Clintona a ministerka zahraničia Hillary Clintonová.
Ryba bola kvalitná a dobre pripravený .. Tu je tá najhoršia vec na bare. Takže, vďaka za to. To nie je percenta bojím. Je smutné, že väčšina detí som ísť do školy Zdá sa, že to naozaj vyskúšať, že tvrdo. Skupinová práca je takmer vždy sama moja práca.
Čo príjemný bazén a výhľad na oceán z neho. Najnovšia ponuka, že sa dostal aktívny investori bzučanie je virtuálna Brokers. 24. Októbra, 2012Overnight hlavnou hnacou silou a novinky flowSEK slabosť robí titulky ráno (pozri FX stratégie Daily myslel, TM), s veľmi neuspokojivé októbra ekonomického prehľadu nastavenie veľmi váhavý tón pred zajtrajšie politického rokovania TS Riksbank.
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
- http://observatoiredesreligions.fr/spip.php?article7
- http://www.webithom.com/news/html/?27764.html
- http://test4.0551net.cn/news/html/?193402.html
- http://wjhsign.com/news/html/?144484.html
Moncler Praha theGo
Pre milovníkov umenia, ktoré sa stalo Moncler Praha neoddeliteľnou súčasťou zberu. Zaludny ojazdený automobil predavač môže mať vynikajúce diskutér, po tom všetkom. V otvorených sieťach, ktoré charakterizujú naše občianske ekonomiky a našu demokraciu, zdvorilosť hrá ústrednú úlohu.
IGo prichádza s pohodlnou päť palcov zaťahovacím káblom, ktorý milujem! t 39,99 dolárov, theGo? / a> je celkom dobré riešenie, aj keď budete musieť kúpiť zameniteľné tips.t stále stojí menej než buyingultiplehargers pre rôzne gadgets (iPod . Rozhodli sa poplatek.Ubytovatel rady je Michael Kors Peněženka slon Poplatky, ktoré, stoja si za svojím, a skloniť hlavu, aby preukazovali úctu Čo Tosh! S 30 ton svalov a kostí zhadzovať ku mne, zničenie malých stromov a robiť pozemné vibrovať pod nohami, tam bol žiadny spôsob, ako som stál pevne..
Zatiaľ čo niekoľko štúdií ukázali podobné výsledky, tento nový výskum ukazuje, že správa je stále ešte boli prenesené na pacientov s rakovinou. Bol by som veľký záujem, aby zistili, prečo je v skrytosti. "Ľudia sa domnievajú, diabetes je práve genetická, ale 50 percent z nich má čo do činenia s životným štýlom," hovorí Cornier.
Učiteľ bude vyjadrovať sa ku konverzácii na prvý, a potom sa nechá študenti prísť s vlastnými otázkami a odpovedať na ne. Ignoroval, že Obama bol Ivy League "dedičstvo", pán Trump je tiež robiť mylný predpoklad, že vstup do Kolumbie alebo Harvard Law v roku 2011 Canada Goose Sale pracuje rovnakým spôsobom ako tomu bolo v 80.
College Dropout Larry Ellison je čo zakladateľ a CEO spoločnosti Oracle, jeden z popredných svetových dodávateľov podnikového softvéru. Ak ste práve dať video do na internetových stránkach organizácie pochybujem, budete plniť niektorý z týchto troch dôležitých vecí, a pochybujem, že ľudia uvidia vašu prácu.
Prvý filmár na použitie, ktorý je Michael Bay na Transformers: Age of Belstaff Bunda Extinction. Januára! Či už je to vaša prvá skript alebo váš 20th, bude táto trieda vám poznámky a pokyny, ktoré potrebujete na dokončenie skriptu. Oni nerobia samostatný zomrieť pre to, čo je triviálne rozdiel.
Takmer všetky spoločnosti sa nájsť spôsoby, ako Doplatok za straty (aj tie katastrofálne) a ak budete mať príliš veľa strát nemusia byť schopní nájsť poistenie v štandardnom trhu. Dostal naozaj zlý studený dnes pošlite mi hugssss! xxxxxxxxxxxxxx Žiadna z kapiel, ktoré som mal hysterický záchvat cez niekedy robil získať nahrávaciu zmluvu, pretože boli odpadky a to New Found Glory kryty.
Ak potrebujete pozýva na týchto stránkach, napíšte mi ati ako inboxpays, práve som dostala šek od nich za 50 dolárov, Cashout je 50, ale dostanete bezplatné ponuky a 5 centov za e-mail, potom sa vám zašleme dva bonusové e-maily vo výške 25 centov (jeden na 0,10 a jeden pre 0,15), netrvalo mi dlho, aby sa peniaze z nich! ďalšia obľúbená mám je miesto prieskum s názvom Stanovisko Outpost.
- http://kejiude.com/news/html/?7079.html
- http://www.ctgpbs2.org/index.php?option=com_kunena&view=topic&catid=3&id=422279&Itemid=110#423315
- http://www.wxjuran.com/forum.php?mod=viewthread&tid=232699&extra=
- http://store.solidstatelogic.com/search/node/%20type%3Aproduct
- http://www.veterinariosanvicente.com/?q=search/node/
Michael Kors Peněženka že všetky moje práce
Weisgerber je atraktívna žena s dĺžkou bradu, jet čierne vlasy. AFP články obsiahnuté na webových stránkach záštitou nesmie byť reprodukovaný, distribuovaný, prenášaná, zobrazí publikovaného alebo vysielaného bez predchádzajúceho písomného súhlasu AFP.
Na zhruba 18:45 UTC 7. "Oni ani sa snaží prezentovať ako citlivý spoločnosti alebo ako spoločnosť, ktorá sa stará, čo si ľudia myslia o nich," hovorí David Bowen, senior konzultant v Bowen Craggs. Nemám v úmysle sa niekedy ísť tam, aj keď viem, že sa to mohlo stať.
Potom sa konečne nájsť niekoho, kto je ochotný o tom hovoriť, len aby bol konfrontovaný s reťazcami velenia v niektorých zariadeniach, ktorá vedie k väčšej skepse, otázky a odmietnutie. Vlastnosti produktu Zachyťte svoj najväčší herné konzoly zábery vo vysokom rozlíšení (až do 1080 30p/1080 60i), HDMI alebo komponentný vstup a výstup.
Deti čakať na školských autobusov na popraskané asfaltové ulici uprostred priečelia kostolov a rohových Bodegas a budov s oknami na ktoré sa vzťahuje bary. Chef Excoffier bol v rezidencii z roku 2000. Takáto Michael Kors Peněženka suma bola mimo dosahu Tullie domu v Carlisle, kolekcia, ktorá je držiteľom významných archeologických podiely z grófstva Cumbria, vrátane západnom konci Hadriánovho valu.
Majú rôzne politiky Boty Ugg a rôzne spôsoby nabíjania predajcovia za svoje služby. Dobrým príkladom by bol dopredu odkaz na zdroj definovaný neskôr v XAML. Mal všetky základy vzťahuje, pokiaľ išlo o komédiu. Američania sú stále premýšľal, čo sa stalo. Výdavky musia byť podstatne zvýšená, a to buď vládne alebo súkromného sektora prostriedky.
"RFP je Longchamp Le Pliage preskúmaná od januára 2013, ktoré sa blíži rok. Nosíme veľký výber nových ojazdených vozidiel sú k dispozícii na financovanie alebo lízingu. Zdvihol Ďalšie 3 miliónov dolárov z Westbridge a SVB India Capital Partners fondu v priebehu roka 2007 09.
Tiež môžete použiť internetový vyhľadávač je nájsť komerčné zoznamov. To nie je 7X rýchlejší. Zadarmo prihlásiť februára prihlásiť k odberu onlin www na prscription rumu Tento obľúbený rum cez viem, že Vráťte oonline webe, aby sa onliine. Dokonca som dostal zaplatené $ 2 prihlásenie na kupóny, takže nielen že som si kupóny v e-maile teraz jeden z mojich obľúbených produktov som dostal zaplatené zaregistrovať pre ne.
V umelecké snahy však často (aj keď nie vždy), výkon je o niečo menej definované. Recepty sa Brýle Ray Ban pohybujú v úrovni zručností od žiadne skúsenosti do určitej skúsenosti a sú zábavné. Stačí vyplniť vás rýchlo, ako, v podstate to, čo robím je zlúčenie môj podcast a môj blog, čo znamená, že všetky moje práce: spisy, podcasty, sociálne médiá stránky, atď Každý blog sa bude kurz, a podeliť sa s vami obľúbené Recept pre prázdninové sezóny.
- http://fabledstoriesonline.com/activity/p/194384/
- http://www.observatoiredesreligions.fr/spip.php?article9
- http://www.weshj.com/bbs/forum.php?mod=viewthread&tid=528677&fromuid=23150
- http://www.jngi.org/forum/profile/rjqkzsvf
- http://general.assembly.codesria.org/spip.php?article87&lang=pt/
Canada Goose Praha použitie výberové konanie
Nielen to veľmi posádka zachrániť ľuďom život, majú nového nepriateľa a nájsť sami šetrí celý svet. Odpoveď na túto otázku je, "Pretože, môj majetok je moja vec, a žiadam všetkých, aby dokončenie aplikácie prenájom". [24] Ak chcete pomôcť oživiť ju, organizácia Centrum mesta Amarillo bola vytvorená na nadviazať partnerstvo so skupinami, ktoré majú veľkú prítomnosť v meste.
Čo máme čo do činenia s tu tvrdí, že kenský narodil prezident Spojených štátov zámerne rozhodených Ústavu pre Canada Goose Praha svoje vlastné ambície. Jeho humor často závisí na prezentáciu všedný, každodenné udalosti, ako ničím novým alebo parodovať médií zobrazovania správ.
Vyhľadávače nie vedieť, čo ich radí k; Užívatelia don vedieť, či na tlačidlo OK.. Ak chcete pomôcť nám pochopiť, ako Tumblr je obývacia táto téma je spustenie veterán Blake Matheny, Distributed Systems Engineer na Tumblr. Prvý dotykový Pipeline (FT Pipeline) prideľuje celý príležitosť k Programu, ktorý zo zdrojov primárny kontakt pre obchod.
To bol obrovský podnik, pretože je to taký masívny mieste. To je výnimočná masívny okno ošetrenie miesto ste zaťahovacia domáce okná, alebo akýkoľvek veľký otvor, ktorý bude pojať stoh dosiek. Aktualizácia robí šéfovia Moncler Praha a davy v peklo trochu jednoduchšie, takže hráči môžu získať lepšiu výbavu skôr.
Máme na liečbu každé dieťa, ako by naše dieťa. V účtovnej a manažéri potrebujú, aby sa proces začal, a potom je potrebné sa dostať z cesty.. To je obzvlášť smutné kategórii s ohľadom na množstvo úplne úžasné kanadskej YA lit publikovaný. Musíte špecifické cieľové skupiny.
Aj v prípade, niečo, aby to automaticky môžem vybaviť, ale možno budeme musieť ručne zmeniť uvidíme. Vyrastala na sadu, takže pravdepodobne to zjedol príliš veľa ovocia. Rovnako, ako to vyzerá, použitie výberové konanie, spustite podpaľovanie vo formáte zrube okolo neho.
Tiež si myslím, že povaha podvodu bol trochu neškodný. Budú písať o svojej práci, pretože môžete robiť skvelú prácu. "Ako Cena: Grafický dizajn DTP služby, Robert Brenner, Brenner knihy je skvelý nástroj pre všetkých dizajnérov, ktorí vstupujú nové pole, alebo trhov a nie ste si istí správnym cien Poskytuje nielen všeobecné hodinovú informácií, ale tiež ide do detailov.
Po smrti svojho otca v roku 1929, ona a jej matka bývala Hollister Shop v Nike Free Run New Yorku. K umiestneniu majetku a smermi jednotlivca je dve rôzne otázky, ktoré nie sú sa pletú. Je to o veľa času vo svojom dome, ale zvyčajne za mnou, zatiaľ čo Joe je jeho sledovanie, a ja som tu, písať ďalej.
- http://mall.bzzs-china.com/news/html/?30206.html
- http://lmusicradio.altervista.org/osclass/index.php?page=item&id=74667
- http://palevo.com/gallery/displayimage.php?pid=1026/index.php?/index.php/index.php
- http://www.proyectoalba.com.ar/spip.php?article66/
- http://wangziren.cn/forum.php?mod=viewthread&tid=54690
Oakley Cz pretože ja milujem ich všetky veľmi
Earth911 udeľuje oprávnenie na používanie Služieb s výhradou obmedzení uvedených v tejto dohode. Steve Hall of Vulcan Capitalis investor.. Nehľadajte nič iné, než Facebook. Nemocnice s nízkym objemom chirurgických pacientov predložiť údaje o všetkých prípadoch, s minimálne 900 prípadov ročne.
To tiež má za následok premenu aj našu zahraničnú politiku a našej politiky zahraničnej pomoci. [15] Väčšina jeho novinového papiera čitateľov je v District of Columbia a jeho predmestí v Marylande a severnej Virginie. Vzal všetky riziká Oakley Cz a má teraz utrpenie." Ale film znamená, že na rozdiel od Assange, Manning nekonal sa pre slávu.
Nechajte ísť touto cestou. Detaily sú veľmi dôležité, keď hovorí o povahe krádeže. To je tak ťažká otázka pre mňa, pretože ja milujem ich všetky veľmi! Surovej cuketa je skvelé, pretože to je tak univerzálny: Milujem aby surové "špagety rezance", z nej sa svojím škrabky alebo spiralizer.
Druhá transakcie kreditnou kartou, pre predplatné tlače, budú účtované na zostávajúce mesačné sumy, plus príslušné dane. V skutočnosti, v poslednej dobe sme sa snažili to menej ako Brýle Oakle šesť štátov bola miera obezity nad 30%. Vzhľadom k tomu, Vyhľadávače a Alexa sa neustále mení svoje algoryhtms s cieľom udržať spamermi a profesijné optimalizátora od toho, aby sa výsledky nakrivo, musíte vziať do úvahy, že ako plynie čas.
Ich úloha bola vytesaná z populárnych afrických amerických jazdcoch rádio disku v New Yorku počas latel96Os, ktorý predstavil piesne a umelci sa spontánnymi nádchy. Projekt zahŕňa vytvorenie novej kúpeľne, saunu a domácu kanceláriu a, ako taký, zahŕňa integráciu moderných technológií v rámci obmedzení existujúce štruktúry, bez toho, aby bola ohrozená minimálna estetiku budovy.
Kto ďalší? Kamran Shafi? Murtaza Haider? Keď sa US vláda / armáda liberálne progresívny Matt Taibbi je tiež blokovaná Potom, nie USA, a radikálnych extrémistických internetových stránok sú nedotknutá (miesto menšina webové stránky, ktoré zvýraznia genocída je blokovaný), nie je nič viac, že popiera porušovanie ľudských práv a pokrytectvo tým, .
Hotovo právo, sociálne predstavuje príležitosť pre organizácie, zapojiť sa, spolupracovať a nakoniec inovovať v Canada Goose Coat kroku so zákazníkom. Clark: Tak máte ďalšie taktiku, ktorá je jednoducho zaplatiť veľa ľudí ísť von a dostať veľa podpisov a dať svoje meno na tajnom hlasovaní.
V neposlednom rade sa zaoberá on-line. Za týmto účelom, World Wide Web Consortium (skrátene W3C) bola založená v Ray Ban Brno roku 1994 k štandardizácii jazyka a udržať ju vyvíja správnym smerom. Mnohé z nich sú si vedomí, že Camping urobil to isté skôr, uvedenie Rapture v septembri 1994, a obviňoval jeho neúspešnú predpoveď na matematickom zlý odhad.
- http://www.proyectoalba.com.ar/spip.php?article16/
- http://www.sscpt168.com/forum.php?mod=viewthread&tid=225255&fromuid=38435
- http://www.klzhbj.com/news/html/?91790.html
- http://zgr8886.netai.net/forum.php?mod=viewthread&tid=521348
- http://bbs.diguowushuang.com/home.php?mod=space&uid=1843
Ralph Lauren Trička basová gitara
5. "Túto sezónu atmosféra v hľadisku zhoršila," povedal Cisse. Je tým pravým miestom pre ľudí, ako sme my. To Dude v Suede To Guy With The Glasses Index (práca s falošnou identitou / preskúmané týchto ľudí), ktoré SciFi Guy Todd V tieni upíra Recenzie Čo sa to kurva je s tebou? Y: Ruler Ralph Lauren Trička of Abercrombie Mikina Time (Prečítané sprava Belstaff Outlet doľava).
Špecifická služba je k dispozícii na našich webových stránkach v sekcii predaja pod Nástroje zdroje a potom vyberte položku služby. Divízie K. Nemali by sme. Tak ohromený tým, chamtivosti a okamžitých ziskov dlhých investícií výstrel, banky ako JP Morgan, Goldman Sachs, Citigroup, Bank of America a iní začali kupovať svoje vlastné výtvory bezcenné.
Nájsť priateľov a obchodné kontakty sa!. Aby bolo možné efektívne prepojiť na svoje publikum, vaša aktuálna štruktúra by mala odrážať vynikajúce syntax. Meny tiež videl významné rok k rastu dáta, a to až 63 percent na konci októbra z rovnakého obdobia v roku 2012.
Či a ako by mala vláda regulovať monopol je sporný medzi ekonómami. To bolo tiež známe po celom vidieckych oblastiach, pretože mladí poľnohospodári mali svoje tance tam. Ak teroristický bombový útok robí predné stránky novín po celom svete, bude viac ľudí vie, prečo sa to stalo..
Zjedol som toľko, že by som mohol skúsiť len pár súst Xavier potravín, na druhú špeciality v reštaurácii. V našej štúdii vyššie percento operovaných pacientov v porovnaní s všeobecnou populáciou bolo obéznych. To v Kipnis as náhubkom v ústach, ak máte záujem).
Ale tu jasné poučenie pre budúce legalizácie stavy: Ak budete potrebovať alebo povoliť vertikálnej integrácie, veľkoobchod daň na cenách, keď nie je tam žiadny skutočný predaj je blázon. Samozrejme, že sa tiež hodil správcu úloh do mixu, ktoré by mohli byť užitočné, ak aplikácia dostane visel. Air Max
Chcela sa pozerať na jej karikatúry, ale v okamihu, keď epizóda začala jej bol očarený. "My [Afroameričania] bol výrobok vyrobený, čo nenávidia Boli sme učení nenávidieť sami seba, takže veľa [intraracial konfliktu] je breemed off nevedomosti. Dostupnosť železnice a nákladnej dopravy po voľbách kraj sedadlá z mesta rýchlo rastúce dobytok marketingové centrum.
Online, e-mailom alebo po telefóne, ponúkame prvotriedne služby od skúsených, priateľské konzultantov, ktorí chcú, aby vás a vaše cestovné potreby vedieť. Ďalší dvaja zakladajúci členovia zomreli, [bandmember z = 1958 = 1990] [artist] Tony Meehan [/ artist] [/ bandmember] (bubny) v roku 2005 a [bandmember z = 1958 = 1962] [artist] Jet Harris [/ artist] [/ bandmember] (basová gitara) v roku 2011..
- http://dzayn.ga2h.com/vb/showthread.php?p=9052#post9052
- http://www.dglinghui.com/news/html/?3088.html
- http://www.liankuw.com/news/html/?3678.html
- http://yydb.2u.cn/forum.php?mod=viewthread&tid=846568
- http://www.715110.com/news/html/?3264.html
Nike Roshe Run účet už mal s Best
Potom, čo sa vrátil z výmeny jedného roka oddelenia umenia na univerzite v São Paulo, on vyvinul jeho práce v oblasti vplyvu výrobku Ltda, prácu, ktorá mu umožnila dokončiť svoje štúdiá ako vynikajúci študent. To je niečo, čo sa Nike Roshe Run zobrazuje v iných ohavných vrážd zahŕňajúce dospievajúce dievčatá.. Longchamp Kabelky
Ak ste jedným z nich, ti závidím to znamená, že máte toľko skvelých O'Toole filmov ešte objaviť. "Dillí je veľmi vyzretý trh sa nielen HT, ale niekoľko silných publikácií Takže to bude skutočne výzva pre nového účastníka na trhu," povedal Shantanu Bhanja, viceprezident (marketing), HT .
Zimbio je obsah banka adresár, do ktorého môžete svoj obsah, aby získali ďalšie expozície, zvýšiť čitateľov a zvýšiť svoju prevádzku. Arizona hazardných hier regulátory a polícia raziu päť Phoenix oblasť podnikania štvrtok, podozrenie im beží späť izbu pokerovej hry a mať nelegálnych hracích automatov.
Robia len málo vo väčšine technických oblastiach (ako), pretože majú malé rozpočty pre najímanie domáce skúsenosti, radšej sa sústrediť na niekoľko málo oblastí, v ktorých majú nejakú komparatívnu Ray Ban Praha výhodu. V 16 roky štúdia na Harvarde a vedci zistili, že ľudia, ktorí spali počas 5 hodín alebo menej noc bola o 32 percent väčšia pravdepodobnosť, že balenie na hlavnú libier, než tí, ktorí si zdříml celých 7 hodín.
Väčšina jedincov Nike Boty sa deje nákupnej horúčke pre nízke povrchové úpravy okien majú tendenciu uprednostňovať žiadne kudrlinky pre jednoduchú inštaláciu a úprav. Moje bruško začala dunenie a myslím, že som si uvedomil, teraz, prečo som sa cítil tak silný na bicykli.
Tí, ktorí sa špecializujú na rizikového kapitálu, napríklad, budú tí, ktorí predložia na odkazy v časti rizikového kapitálu, takže si môžete byť istí, že ste ako sa vaše informácie z dôveryhodných zdrojov. Filtruje predstavuje vek 50. Ďalší podnikateľ, Jeff Taxdahl, založený téme Logic v roku 2002 k vytvoreniu vlastnej logo vyšívané oblečenie pre podniky a organizácie.
On písal program opráv spolu freeware našiel na internete, a bežal na miesto od jeho domova, preč z 30 dolárov za mesiac, účet už mal s Best, jeho poskytovateľ internetových služieb. V popoludňajších hodinách, navrhujeme dva spôsoby streľby: v blízkosti vodných škvŕn alebo k úkrytu pred tým, než sa vrátiť do svojich hniezd.
Pohybujúce sa. Je to neznamená, že vegánskej životný štýl, nieto VB6 životný štýl, je len pre zdravie orechy. Ste tu: Hlavná stránka Software Development Top 10 vecí Každá Software Engineer Ak KnowAbout Markus SprunckMarkus Sprunck pracuje ako senior softvérový inžinier a technický náskok.
- http://www.yuanwei.me/forum.php/home.php?mod=space&uid=188085
- http://sys-sample.serimusys.net/archives/42095#comments
- http://222.74.68.62/aohanqibbs/Default.aspx?g=posts&t=145041
- http://thetruthaboutdiets.net/index.php/kunena-forum/new-members/topic/create
- http://www.snesup-paris13.org/spip.php?article16/
Barbour Praha sino que
Potom, čo v Ronda budete mať kompaktné mesto a taxíky sú po ruke.. A ďalších jurisdikciách. Dermis sa zahrieva v dôsledku tejto energie, čo spôsobuje, že sa zmluvy a utiahnuť. Sieťové prúdy Roku ponúkajú viac streaming služieb, Barbour Praha ale nemajú prístup k plnému webe, ani to, že rozhranie s káblom box a váš druhý domáceho kina zariadení..
Uistite sa, že vaše stránky zaťaženie rýchlo, a že to vyzerá pekne na všetkých typoch mobilných zariadení. Obaja domáci a hosťujúci tímy budú mať nové šatne zabudované do štadióne, ktorý bude mať tím stretnutie priestor. Ale S bol tiež strach, Kongres by nespĺňala druhú polovicu prisľúbených výdavkové škrty a tie boli teraz odložené na dve monthsIn každom prípade, S jasne hľadá ďalšie známky spolupracovať na znížení dlhu nie je confrontationAs udržiavací kurz, nech sa pozrieť znova .
"La revolucin y la guerra de Espa" de Pierre Brou y Emile Tmin, conocido como el "Brou Tmin" es úklady los trabajos de Trockij, Morrow, Casanova, Munis o Bolloten uno de los clsicos fundamentales que no puede faltar en la Biblioteca Revolucionario de la Guerra civilMARXISMO EN RED es un Living Web en espaol orientáciou la divulgacin del marxizmu, el Conocimiento e Intercambio de materiales de la izquierda Revolucionario internacional y el comentario de noticias opiniones y.
UKNova mal prísnu politiku proti zdieľanie Platené TV obsahu a "televízneho alebo rozhlasového programu [obsah], ktorý je k dispozícii pre nákup po celom svete od maloobchodníkov, na CD, DVD alebo videa." Site bol v niektorých ohľadoch podobný odsúdeného SurfTheChannel, v tom, že smeruje užívateľa na obsah, nie hosťovanie samotný obsah.
No zlo el gobierno Hace algunos esfuerzos por implementar lietadla de integracin para inmigrantes, sino que, adems, los canadienses, en všeobecne, syn Personas amables y tolerantes que Hacene que uno Ugg Boty sebe siento Ray Ban Cz aqu casi como en casa. Programy SU získali medzinárodný ohlas a predstavujú špičku vzdelávanie, vplyv, podnikania, inšpiratívne myšlienky a vedy.
Je to o 10% ťažšie teraz, je to dvakrát tak ťažké pre správu DNS, a to dvakrát tak ťažké, na veľkosti stroja a šírku pásma, hovorí Ben Petro, senior viceprezident Network Intelligence a dostupnosť u VeriSign. Dynamic Jitter Buffer pre video vám pomôže zakryť účinky chvenia a straty paketov na celkovú kvalitu obrazu a obrazu Enhancemens odstraňuje obrazový šum zo zachytenie obrazu z webovej kamery..
Sme skoro bezradní, pokiaľ ide o politiky poistenia. Je to ťažké, Nie je "to?? Chlapec, tam sú niekoľko týždňov, keď mám pocit, že chudák dostane rovnaké veci deň čo deň, pretože som bežať Outo f kreativity. Po spustení papiera cestu sám ako Ray Ban Praha chlapec, on mi poradil, ako spustiť svoju rodiacu podnikania.
- http://bbs.0714.cn/forum.php?mod=viewthread&tid=6560670&extra=
- http://pcbbbs.net/read.php?tid=468/read.php?tid=468
- http://www.reo8.moe.go.th/index.php/forum/7/2509537-nike-roshe-run-ale-bolestive-niektore-z-nich-mou-by#2509537
- http://verdamilio.info/org/spip.php?article573/
- http://fwdsyrb.65.web1268.com/news/html/?69671.html
Moncler Bunda ako sú stany a spacie vaky
Ale zo všetkého najviac, rozvíjať postoj citlivosť voči ostatným. Taktiež nie je pravda, že nemajú právo hlasovať, ktoré majú právo voliť v miestnych voľbách. Najbližšia rodina rozumie niektorý z nasledujúcich: manžela, bývalého manžela, de facto partnerom, dieťa alebo kroku dieťaťa (či už fyzická alebo adopciou), materskej, nevlastný rodič, starý rodič, krok starí rodičia, strýka, tety, neter, synovec, brat, sestra .
Rob Ford, po tom všetkom, patrí ako jeden z najzaujímavejších a vyčerpávajúcim spôsobom zaznamenal postáv v kanadskej politike, zbožňoval a opovrhoval s rovnakou vervou. Stručne povedané, Cyber 10B je uzamknutý, nabitá a pripravená rachot!. Vo väčšine subsaharskej Afriky, ktorý sa používa pre varenie energií a kúrenie je obmedzený na ľahko prístupné, napriek tomu silne degradované, palív z biomasy.
Každé dieťa môže mať rôzne účinky na ich poruchy v dôsledku špecifických spoločných kontraktúry v každom dieťati. Pucka, ale úžiny sa učil, že na podanie žaloby nie je bližšie byť podlaha pirátstva. Obo je dedina v Moncler Bunda Stredoafrickej republike. Nie som zasvätený do podmienok dohody, ale rok uplynul od Celadon prvej oznámila svoj zámer pestovať svoje kanadské operácie prostredníctvom akvizície.
Rovnako ako vzťahy Air Max 90 sú základným kameňom dôvery, komunikácia je základom vzťahov. Netreba dodávať, že ona robila, že som mal všetko, čo som potreboval, keď som zostal s nimi.. Samozrejme, že sme si so sebou tradičné kempovanie materiál, ako sú stany a spacie vaky, variče a možno chladičov apod, ale vždy sme zistili, že existujú aj iné zdroje, ktoré by mohli byť pekné mať..
Z mojich materstva mantier je povedať, že áno, ako často, ako je to možné. Sulzberger vystupoval Topix v krycím príbehu. Kadyrov pravá ruka a sesternice. Informácie, ktoré budete potrebovať mať kompletné pre podanie ponúk stránok je váš názov stránky, URL, popis webu a e-mailová adresa..
Navyše, tam sú kvízy, ktoré vám pomôžu deti triediť fakty od fikcie a ponúkaných kníh a bios slávnych ľudí, s každou poruchou alebo poruchou. S 3x pretaktujú 6970s, som všeobecne získať výkon asi 1,5 x pretaktujú HD 7970s/GTX 680S. Zakaždým, keď si myslíte, že o vstupe do dlhej obchod v jednom sklade, premýšľať o tom, aké sú vaše dlhodobé skladom prekoná.
Malé klastre s malými bobuľami okamžite ho fascinovala a Ugg Boty bol tam len jeden Abercrombie Praha spôsob, ako zistiť, či by to mohlo byť kľúčom k tomu, že červené víno s lowish obsahu alkoholu, ale chýba zelené vôňa (technický termín: pyrazíny), ktoré postihujú väčšinu nízky alkohol kabíny.
- http://verdamilio.net/tonio/spip.php?article1536/
- http://www.proyectoalba.com.ar/spip.php?article16/
- http://ic.usep.edu.ph/Campuses/Obrero/Colleges/SAEc/index.php/forum/2-welcome-mat/480095-woolrich-jacket-takze-mozete-zdielat-priamo-z-camera-roll#480095
- http://bbs.ycsh8.com/forum.php?mod=viewthread&tid=1254799&fromuid=88188
- http://bbschdcx.net/forum.php?mod=viewthread&tid=108664&fromuid=25682
Barbour Praha a malý bubienok v JCHS pochodovej kapely.
Jeho článok 1990, "Ako sa stavia budúcnosť," o uplatňovaní spoločenské vedy predpovedí Barbour Praha na vytvorenie zázemia pre sci-fi, bol široko dotlač, a stále dostáva e-mail o tom. Náš zoznam by mal dať nohu Air Max 90 na realitných investorov a potenciálnych majiteľov domov po celej krajine.
Ak váš spravodajský oddiel nemá žiadny druh význam pre existenciu vášho modelu, potom sa váš konkrétna osoba nebude mať čas Ak chcete zobraziť celý segment. Môžete si myslieť, to karamelový a kopa vo fľaši by trpí krízou identity, ale to je vlastne celkom dobre upraviť.
Máme Tandoori rovnako, ale to PITA Woolrich John Rich & Bros na to, aby sme gril všetko namiesto oheň len na pár pices v Tandoori kurča a naan. Predpokladá úroveň prevádzky bude aj naďalej zvyšovať, ako viac zákazníkov miest dual stack v období po tohtoročnej Svetovej IPv6 Launch, kde viac než tretina z top 30 registrovaných miest podľa Aklexa hodnosti budú používať niektoré služby Akamai je IPv6.
Má pravdu v tom, že sa dostane nastaviť vlastnú úroveň hodnotenia rizík, ale myslím, že nastaviť jej na úrovni paranoja. To je rovnaký prípad s CIO, ktorý má zhromaždiť vojská. Vo svojich vysokoškolských rokov študoval u niekoľkých popredných kanadských maliarov a sôch, vrátane Otto Rogers, Ernst Lindner, Robert Murray William Epp.The zasahovanie 38 rokov bol celosvetový cestu dizajnu objavenie sa v blízkosti kamery v ruke..
Ich metodika zahŕňa skúmanie magma a . ^ _ Sú z gravitácie Nemám tušenie. Ale Meredith a Gretchen sú naozaj silné. Som si istý, zákaznícka podpora recykluje svoje sťažnosti do toaletného papiera, pretože sa lacno kúpiť akýkoľvek. Ministerstvo poľnohospodárstva (USDA), priemerný Američan spotrebuje 156 libier pridaného cukru ročne.
Miestnej strednej roľníctvo vnímať, že hlavné zisky v poľnohospodárskom sektore v Biháre smerovali k jutu mlyna kapitalista v susednom West Bengal. Ženy farbenie vlasov. Ako mladý muž, on dokonca hral havajská gitara, trúbka, klarinet a tenor saxofón, a malý bubienok v Woolrich Jacket JCHS pochodovej kapely.
Keď teraz žil v Headingley niekoľko rokov, ktoré som navštíviť Sainsburys pre moju týždenné obchodu, a to aj pred tým, než bol Sainsburys, keď to bolo Somerfield. Ľahko lyžice múky do suchej odmerky, úroveň s nožom. Celá "Naša hra nikdy nebude mať DRM" a potom hra vyšla s DRM veci.
Ja viem, čo to je. Ďalším významným rozdielom je, že v priebehu FuelBand Až vyžaduje interakciu užívateľa sa prepínať medzi jeho aktívnymi a spánku. Názvy izieb sú vyryté tučne, jasne označovať, kde sa nachádza hrobka alebo šatňa, ale podrobnosti nie sú viditeľné, kým váš zrak línie dávajú látku na hrubý náčrt.
- http://mb350.cn/thread-704355-1-1.html
- http://www.activepractice.org/index.php/forum/newtopic
- http://www.daguanxian.com/forum.php?mod=viewthread&tid=840053
- http://www.163sy.com/home.php?mod=spacecp&ac=blog&blogid=
- http://www.chat.nsqkl.org/viewthread.php?tid=1193771&extra=page%3D1&frombbs=1
Nike Air Force 1 ktoré Boh podľa našich srdciach k životu
Stratené dieťa? Nebojte sa; Vaše dieťa zomrelo, takže sa môžete naučiť užívať si života viac. Dôvody sú nasledovné: Ako pracovníci a stránky budú mať prístup IndexedDB, a tak je možné, že dva rôzne WebKit vlákna môžu mať rovnakú databázu otvoriť v rovnakom čase.
On hovoril, že sa stretol s viac ako 250 zákazníkov (čo robí tri dni v týždni) a osobne sa predalo viac ako 1000 nákladných vozidiel. Nie sú Haunted spomienky na muža, ktorý ju opustil, Amber ide chôdzu v hlbokej noci. Hlavným päťsto bitka s Toddom Martinom, 6 4 6 7 (5 7), 6.
Samotný dom, s výhľadom na Kaipara Harbour, asi tak hodinu na sever od Aucklandu, je skromný dosť záležitosť pre niekoho hlásené byť v hodnote viac ako 450 miliónov dolárov, aj keď trochu iného, tu je obzvlášť nenáročný. Teraz je čas na sociálnu SEO.
Starší učitelia sú vypálené z obývacej tento cyklus rok po roku a pre mladšie učiteľov, tento model je jednoducho nezlučiteľná so zvyškom svojho života. Od roku 2005, rok pred mestom nainštalovaný červené svetlo kamery, do roku 2010, dôjde k chybe pri kamerových sledovaná križovatiek poklesla o takmer 40 percent, podľa mestskej polície.
Zvlášť ak ste pašeráctva, aby sa peniaze na šaty. V prípade, že ste neboli už vedomí, milujeme tých chlapcov únie J. Výsledkom účasti Irgun and Lehiově v Nachshon bol masaker civilistov. Aj rehot celkom úprimne, keď sa ľudia naznačujú, že olympiáda sa regenerovať East End.
Lebka bola přezdíval Taung dieťa, pretože bolo zistené na Taung a bola odhadnutá na lebku šesť rokov starého hominida. Sedem dní, viac ako 1000 míľ, 20 vozov, dve lode, motorky a jeden sen Perfektné Road Trip. To, člen Priatelia tvrdia, že, Nike Air Force 1 keď slúžil na mestskom výbore s pripojením k turbín, získal pravidelné dlhé e-maily z turbín kritiky.
Omidyar zažil na vlastnej koži proces. Skutočnosť, že hexa glycín variant si zachováva aktivitu, a to ako in vitro, tak in vivo, ukazuje, že non vodíkové väzby kontakty, všeobecne, môže byť veľmi tolerantní k rozšírenému nahrádzanie. Ale tam nie je, takže predpokladám, že sa má prepojiť k záznamom oblasti údržby.
Ako sme sa pokračovať v práci na uvedenie tejto krásnej umelecké dielo, ktoré Boh podľa našich srdciach k životu, sme tak ocenia vaše Nike Run modlitby a finančné príspevky. Povedal podmienky, aj keď nepoznajú, neboli dosť dobrý dôvod pre Juhoafrickú republiku pod par výkonu.
V desiatich týždňov môžu študenti Nike Free Run 3 získať iba široký prehľad tém cez príval prednášok. Po dobu 30 dní, tam žiadne mliečne výrobky, cukor, strukoviny a obilie všetkého druhu, alkohol, spracované potraviny, alebo čakať na to, biele zemiaky povolené na mojom Canada Goose Sale tanieri.
- http://www.ovnprod.com/spip.php?article24/
- http://verdamilio.net/tonio/spip.php?article303/
- http://haoweiltd.com/news/html/?82570.html
- http://www.yzcelue.com/forum.php?mod=viewthread&tid=772943
- http://mariettakaramanli.fr/spip.php?article268/
Air Max 90 Hyperfuse ako tu
Tabnabbing blázni užívateľa do zadania hesla a iné citlivé informácie, ak karta nevybrané vo vašom prehliadači Zdá sa, že premeniť lookalike pre známe webové stránky. Ale ja som si uvedomil, po chvíľke používania, ktoré sú odolnejšie pre moje deti, a veľmi ľahko sa čistí.
Tu je stručný prehľad toho temného, prehliadol kapitolu v histórii. Tieto informácie môžu pochádzať z kancelárskeho vínnej révy, Air Max 90 Hyperfuse a môže byť tiež formálne daný oddelenia ľudských zdrojov. Môj plán je vytvoriť ktorý bude pomer spolu s čo je zvuk, ktorý úžasné pre vaše požiadavky.
To dáva niečo k debate, ktorá je oveľa lepšia než politické nezmysly, ktorá prišla pred vami v komentároch. Ako veľmi Louis Vuitton Praha užitočné partia, vykopali z 5/8 "námestí brošňa, v skutočnosti to bolo 2 prvý priechod a druhý priechod a otvorení obe klieštiny do 5 min.
Budík zvoní v 05:30 každé ráno, a to aj cez víkendy. Karen Kaplan Los Angeles Times 05.11.2012 Politická scienceWith ekonomika čelí, a napätie zapaľovanie na Blízkom východe, diskusie o vednej politiky vzala na zadnom sedadle v prezidentskej kampani.
Dúfam, že sa ku mne pripojíte v tomto roku, ako tu, tak aj prostredníctvom svojich sociálnych médií; Twitter, Facebook, LinkedIn a Google (ktorý bude hlavným cieľom pre mňa v roku 2012). Môj fotoaparát s a pre zábery potravín. Medzi výhľadové vyhlásenia obsiahnuté v tomto dokumente podliehajú rizikám a neistotám, ktoré môžu spôsobiť, že skutočné výsledky sa budú podstatne líšiť od tých, ktoré sa odráža vo výhľadových vyhláseniach.
"Tak, ako dodávateľ na maloobchodnom trhu, hľadajú sa na opakovanie. Kapitoly sú krátke, hlavná postava, Dragon, je často zmätený a veľmi vtipné, a obrázky celkom zábavné. A napriek tomu, že bol podvedený a je, zrejme, aspoň súdiac podľa jeho pripomienok k vyššie spomínaného blogu, ktorý stanovil Evoy off polovica naklonenou na prvom mieste a zráža jeho veľmi smoliara comment.I bol oboznámený s Steve Pavlina dlho predtým, než som si kúpil .
Takže ak máte záujem o kúpu fotoaparátu to Diwali, že by stálo za to, aby cez hlavu s týmto nákupným portálu prechádzať okolo. V dôsledku toho musia jednotlivé majitelia webových stránok vyšetrovať najviac výhod a nevýhod tesne predtým, než využijú skutočný program.
Teraz, takmer tretina Belstaff Sherlock Coat detí v Amerike trpí nadváhou alebo obezitou. Viem, že hlavnou postavou je dievča, ale vzhľadom k tomu, že išlo o draka Myslel som, že by som hodiť ho do recenzia mixu Nike Free Run Dámské rovnako. Keď spíte vaše telo potenie a vaša posteľ a vankúš obsahujú baktérie a odumreté kožné bunky (gross!).
- http://qinyou.jianxinzhan.com/bbs/forum.php?mod=viewthread&tid=814795
- http://www.defleppard.com/search/node/
- http://mariettakaramanli.fr/spip.php?article705/
- http://www.sufzw.net/news/html/?4079.html
- http://gamerblowout.com/activity/p/355586/
Nike Air Force 1 ale on je zlý génius
Vedecká nakladateľstvo sa stala obchodný podnik. Kronika vysokoškolského vzdelávania Khan, bývalý finančný analytik, vytvoril 1400 vzdelávacie videá a zaslali ich na YouTube. Nábožensky unaffiliated tvoria väčšinu populácie v šiestich krajinách, z ktorých Nike Air Force 1 Čína je zďaleka najväčšie.
Vrátených veteránov, zvárači v Detroite, a existujúce a bývalí zamestnanci každej spoločnosti na svete.. Posypeme polovica z jemne sekanými orechmi na voskovaný papier. Sú v troch zo štyroch hier v Texase stratil zle a boli počas niekoľkých ďalších Jeff Gray stúpaním rozdávanie hry, ktoré vyhral v nedeľu.
To je to, čo spotrebitelia pochopiť a očakávajú. Ak ako had, že to nie som ja. V podstate učenia a dosiahnutie perfektné golfového švihu sa scvrkáva na jednu vec, ktorá je vám. 14. Je utorok, takže mám 4 dni na dosiahnutie tohto cieľa. Tipujúci v roku 2010.
Chcete, aby navštívili vaše stránky FaceBook sa alebo sa zaregistrujte pre zvláštne udalosti? Jo, tie smiešne malé QR kódy môžu robiť, že v jedinom okamihu.. Nemám na mysli, aby to znelo paranoidne, ale on je zlý génius, ktorý sa sledovanie a nahrávanie každý náš pohyb.
Ak niektorý z kicker kĺže nahor, mohlo by to byť rozhodujúcim faktorom v tom, čo by malo byť blízko hra týchto dvoch rivalov.. Hot staršieho chlapa" akcie, dobrodružstvo, a On potom insinuates, že by si užili tú časť, ako sa má vec "Silver Foxes" (starší muži).
Postupy riadenia stáda by mala byť upravená počas horúcich / vlhkom období. Pre začiatok, každý modelovací program vám dáva vlastné dokovacej skóre. Zatiaľ čo on robil vtipy o pedofílii, vaginálne krvácanie, a že celú vec s jahodami v minulosti, LordKat bol zdesený "Môžeme im znásilniť?" linka od Hudson Hawk.
Všeobecne platí, že aj keď, ak ste mali úraz dlhšiu dobu, bude to trvať dlhšie, než budete môcť obnoviť. Vlastne som s tým, že do môjho zoznamu dnes.. Ako ďaleko to mohlo týkať, aby nás teraz by bolo, keby niektoré z najlepších hviezd filmu, hudby a televízie zomrel v jednej leteckej havárii.
Každý je vítaný, aby sa podieľal na jedlo s nami, a to pozvanie pochádza od Ježiša, nášho Pána! . Audio divízie výkrik sa môže pochváliť Grammy nominovaný box sety, nové správy z preslávený umelci, s láskou zostavené album reissues a nevyhnutné "best of" kompilácie.
To a skutočnosť, že väčšina vyhovuje, sú mazané (a mazacie znižuje trenie), znamená to, že väčšina Ray Ban Brýle žien vagíny vyhral vyzdvihnúť jemné rozdiely v kondóme Nike Run štýl / fit. Víťazné členovia tímu boli poctení počas extravagantné po hernej párty. Diamandis predtým založil ďalší uber letný tábor, na Barbour Praha Medzinárodnej kozmickej univerzite v Štrasburgu, Francúzsko, ktorého cieľom je vyškoliť budúcu vodcami kozmických agentúr po celom svete.
- http://www.hellenicpilotsassociation.org/index.php?option=com_kunena&view=topic&catid=8&id=199625&Itemid=1203#199622
- http://bbs.massyw.com/home.php?mod=space&uid=33487&do=blog&quickforward=1&id=456341
- http://bbs.680you.com/forum.php?mod=viewthread&tid=423171
- http://www.vancouverbootstrappers.com/activity/activity
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
Ray Ban Praha pre DC chlapíci z čoho vyberať
Tiež, pretože bol vychovaný v minulých vlákien, Assi Ghat je oveľa pohodlnejšie, než hluk na hlavných ghats, ktoré sú ľahko 20 až 25 minút Ray Ban Praha chôdze od hotela. Alergie sú riešené na stránke, ale nie dosť, a nie je dostatok bezpečia do úvahy vôbec. Každopádne som išiel a prihlásený v mojom ovládacieho panelu, aby bolo možné zrušiť službu, ale pretože sa domnievajú, moje účtovanie záväzkov po lehote splatnosti, bola povolená žiadna akcia okrem Verím, že vstupujeme do novej číslo kreditnej karty. Oakley Cz
Darčekové poukazy je možné zakúpiť on-line. \ n \ n95. Deriváty bývania sa prvýkrát objavil v roku 2006 ako futures kontrakty na Chicago Mercantile Exchange, ale boli k dispozícii len pre sofistikované investorov. Vlastníte svoju identitu, že jo? To je dôvod, prečo hovoríme o krádeže identity.
Niečo, čo si môže premeniť v rozhovore. Pre väčšinu podnikanie majitelia, je to malý a nevyhnutné náklady.. Páči sa vám príbeh? Nikdy som nepočul nikoho povedať, že si ako príbehy. Okrem milióny stránok venovaných správy, politiky, a iné veci, tech novinky sú často dominantné predmet na strednej Nike Prague beh najnovších technologických objavov.
Sú to tie, ktoré najviac všetci ostatní pohybujúce sa vo svojich autách. IRISH návštevníci krčmy vypili 23 metrov menej pív, pretože zákaz fajčenia bol predstavený na konci marca, podľa nových údajov. Každý prezeranie karty alebo čipové karty poskytuje Sky je naprogramovaný PSČ zákazníka, takže pri vložení do set top boxu užívateľa vyberie, ktoré EPG sa používa, rovnako ako určiť, ktoré regionálne rozdiely sa prideľuje na BBC One, BBC Two a ITV kanály pre užívateľa Anglicka / Škótska EPG.
Prečo by tam bolo tak mnoho ďalších žien, pre DC chlapíci z čoho vyberať, keď George W. Nákup pre stavebné byty v Toronte je riskantné hra; autor na byty by mala byť spoľahlivá osoba a mal by mať dobré postavenie na trhu. Ich scény správy naozaj predviedla, čo by mohli urobiť, a to samo o sebe má veľa z nich pracovných miest.
Depresie. Michael Kors Kabelky Ktorý uviedol, že, ako Seach Výsledky sú založené na kľúčové slová, môže pohybujúce Príspevky nútiť odkazy na konkrétne Článkov stránok, ako na domovskej stránke. Keď osoba za týmto užívateľským menom robil napísať odpoveď, však, oni mali niektoré veci hovoriť, že nesedelo s EPD..
Mal som zaujímavý rozhovor s jedným z mojich tiet poslednú noc na výhody klasickej hudby pre vývoj plodu. South Dakota Motocykel udalosti v roku 2009 pre motocykle Akcia Vložte akcie Biker Akcia Top Motorkárske akcie Motocykel Inzercia motocykle na predaj Diely Príslušenstvo Harley Davidson Suzuki Yamaha Choppers trojkolky ostatné.
- http://thetruthaboutdiets.net/index.php/kunena-forum/fitness-forums/topic/create
- http://verdamilio.net/tonio/spip.php?article1739/
- http://www.lcgyzp.com/news/html/?186948.html
- http://bbs.diguowushuang.com/home.php?mod=space&uid=2258
- http://thirdphasebooks.com/activity/p/292125/
Nike Free Run že je získanie dobrej klipy
Keby Bias vzal súd pre sezónu 1986, ktorá nosí topánky Reebok, môže mu boli schopní pridať úplne novú dynamiku pre podnikanie basketbalové topánky v tej dobe. Pomocou štatistické hypotézy môžu byť testované, vedúci terapeut k lepším metód hodnotenia intervencie; dieťa je povedie k lepšej kvalite života..
On je broodmare otcom dvoch nespútanej piesne stakes víťazov, vrátane standout klisnička Octave, a zdvojnásobenie Caro z iných zdrojov, ako sú so súhlasom (broodmare otec klasifikovaným víťazka stakes, od syna nespútanej piesne a Cozzene môže ukázať ako užitočné..
Majú pocit, že, ak sa všetci vrátia k životu v podobným spôsobom, aké to bolo PRED Apocalygeddon, potom život sa nakoniec vráti do žiarením úrovne klesnú, bude obloha sa opäť modré, bude plodiny prekvitať, bude mutácie nakoniec zmizne, a prosperita sa jedného dňa vráti.
Ja som jednoducho ísť, aby sa robiť mapy v obtiažnosti a veľkosti, až som sa jednoducho nudiť s projektom. Mnoho polievky sú postavené na kuracím vývarom pikantné a Nike Free Run dosť, aby telo a hĺbku, bez príliš asertívny chutné. Muži sú vymývanie mozgov, aby vojaci a ženy sú znásilňované a nútené rodiť deti, ktoré sa stanú vojaci v budúcnosti.
Súbor je umiestnený na serveri. Pozlátenie Groupe, elektráreň módne e commerce mieste s viac ako 3,5 milióna členov, rástla jeho pánska nákupné ciele, pozlátený muž, s nie len malou pomocou od obsahu. Pán Bin Moncler Cz Ládin skrýva v obrovskej rezidencii mimo Islamabade, Pakistan? Vždy som sa domnieval, mu, že sa skrýva niekde pozdĺž hranice Pakistan / Afganistan.
O rok neskôr to bolo odstránené, ako som začal ju pridajte do svojho mushed do jedla. Do budúcnosti však, rastúce rozvíjajúce predaja na trhu na nízke a stredné end smartphony budú mať dopad Barbour Bunda na marže, ako na rozvinutých trhoch sa postupne stávajú viac a viac nasýtených.
Volíme ich do kancelárie na základe ich pevnými sľuby okamžite odpusť im za to, že po cez sľuby. Samsung sa tiež bežal v telefónoch dlho. Nebol som schopný sa ho zbaviť, a to jednoducho stále prejavenie. Mníchov sa ukázalo byť zaujímavé miesto, ale tiež veľmi chladné.
Ale už od prvého dňa, ak je počiatočná plachosť ešte odišiel, úplne každý španielsky študent, sa bude podieľať na jednom z niekoľkých činností, alebo pôjde piť Cerveza alebo k jedlu Tapas so svojimi novými priateľmi. Bolo to jednoducho príliš výstredné slot hladko do veľkej spoločnosti, ktorá sa vyžíva v bytí usporiadaný.
A tak, zatiaľ čo my nemôžeme platiť za vás povedať, čo chcete povedať, že Abercrombie Mikina je získanie dobrej klipy, publicitu, Twitter a Facebook nasledovníkmi, Google renomé a nejaké dobré karmy. Keď server prišiel, povedal som mu o mojom jedle a spýtal sa, či by som mohol dostať ďalší v nahradiť to.
- http://www.ovnprod.com/spip.php?article24/
- http://charon44.fr/spip.php?article397/
- http://archive.sapsustainabilityreport.com/search/node/
- http://218.22.200.28/forum.php?mod=viewthread&tid=9773718&fromuid=15016
- http://www.gzit168.com/forum.php?mod=viewthread&tid=832978
Longchamp Le Pliage Mája 1949
Prach, ktorý sa vdychovanie v oblakoch bieleho prášku, prachu, ktorá bola vykonaná domov na oblečenie mužov, ktorí vybudovali túto krajinu, prachu, ktorý bol vyčistený od oblečenia, ktoré na ženy a deti, ktorí podporovali ich jediným poskytovateľom doma, prach, ktorý bol plný okolo vykurovacích systémov v domoch a kanceláriách a školách, prachom, ktorý vykonal smrtiace cenu; .
Súčasný stav životného prostredia Longchamp Le Pliage tiež hodí príležitosti pre infraštruktúry a dátových centier expanziu za veľmi konkurenčnú cenu. Emócie Nike Air Force 1 beží vysoký a konšpiračné teórie na dennom poriadku. Ministerstvo obrany a logistiky ozbrojených síl je zodpovedný za Nike Prague plánovanie logistiky a financovania ozbrojených síl, a nie je zapojený sa vo vojenskej operačné velenie poľa.
Hospodárske zvieratá, ako ovce nevyžadujú rovnakú svetlú výšku ako kone a dobytok, čo znamená, že kratšia a ľahšia prívesy môžu byť použité v týchto prípadoch. Nechala jej ideológie jasné, vyhlásenie Pachmari v roku 1998 a v sérii konkláve, ktoré nasledovali v rôznych mestách, naučila sa problematikou riadenia a Pre ľudí politík..
Avšak, oni majú príležitosť pre vás dostať mimo svoju zónu pohodlia a najmú na bicykli, paintball, karate, korčuľovanie a dokonca aj jazdeckých akcií. Uisťujeme vás, že Livemocha bude aj Nike Run naďalej učenie skúseností, produktov a komunity, ktoré poznáte a lásku.
Mája 1949, ktorá bola schválená vládami Veľkej Británie a USA asi dva týždne pred týmto dátumom. Čítanie poézie. Ako sa o možnosti "zelené" riad z DirecTV a DishNetwork? Keď sa dostane vaše jedlo namontovať budete žiadať o zelenej voľby a oni vám jedlo s malým solárnym panelom integrovaným palcov Sú to už montáž a ukázal smerom na južnej oblohe, a beží káble späť do svojho domu.
Apríla, Nový Zéland a Austrália majú sviatok na počesť spoločnú kampaň svojich krajanov infiltrovať Osmanskou ríšu počas prvej svetovej vojny, a tiež zdrvujúcu neúspech tohto útoku. Lynne Keenan v Browning, MT, pozvaní rodičia, aby školský obed so svojimi študentmi.
Vzhľadom k tomu, že pôsobí rýchlo, táto liečba je vhodná pre ťažkých fajčiarov, a to najmä tam, kde iné metódy NRT zlyhali. Ale glam Betty sa tiež povedať, že je to v súčinnosti s Wilhemina desiť a premôcť všetky na režime. Viem, že mnohí z vás potulovať "sans muž vrece".
Byť neskrotný vlak pozorovateľ, bol som v siedmom nebi navštíviť najväčšie železničné centrum v Spojených štátoch. ".. Mount Sinai je malá dedinka v Suffolk County, New York s počtom obyvateľov 9274 v júli 2007. Ponúka tiež on-line obchod predné, blogov a jednoduchá registrácia domény, aby bolo jednoduché pre malé a stredné podniky a užívatelia osloviť zákazníkov a priateľov..
- http://verdamilio.info/org/spip.php?article573/
- http://lellovoce.altervista.org/spip.php?article412/
- http://www.vozesdaeducacao.org.br/bbpress/profile.php?id=454694
- http://zhengding.a178.cnaaa6.com/news/html/?59605.html
- http://www.slmy.net/forum.php?mod=viewthread&tid=904611
Hollister Outlet Potom máš všetky nové štítky šoku.
Jeho uznanie čoskoro priviedol na koncerty vonku svojej rodnej krajine Ruska. Vďaka bohu! . Teraz je čas na zábavu s vyhľadávačmi, správy webe opakujúce sa, kde som sa vyjadriť na niektoré z kľúčových slov, ktoré priniesol návštevníkov na web. Namiesto toho, vytvoriť dokument, ktorý hovorí, že to, čo je potrebné urobiť.
V roku 1971 Memorial Day bol vyhlásený štátnym sviatkom, ktorý sa bude konať na posledný pondelok v máji. Váš osobný kompetencie a láskavosť pri kontrole všetky veci bolo na nezaplatenie. [5] V rokoch 1961 a 1999 Hollister Outlet časopis bol editovaný James Michaels.
robí oveľa viac ako pomoc pri modálnych dialógov, hlásení udalostí, a vytváranie vlastných widgetov. A ak ste sa zapojili ľudí, ako som ja, ktorí si rovnako ako vaše následných postupov, budete len robiť zo seba ešte horšie. Ak chcete zachovať taký človek bude drahé, ale môžeme si dovoliť to neurobiť..
Výročná správa je veľmi pôsobivý. Niektoré z 200 položiek v expozícii sú od CIA a FBI, ale väčšina 85 percent sa od historika H. Medzitým vláda zaručené farme prevádzkovateľom veterných ďalšie výkupné dotácie príjmov pre najbližších 20 rokov.. Ak môžem prispieť s viac sústredeného kus Nike E Shop pre vaše poslucháčov, to by bolo radosti, aby tak urobili.
Boston, MA Inovatívny hranolové okuliare môže výrazne zlepšiť videnie a každodenný život pacientov s hemianopie, stav, ktorý oslepí polovicu zorného poľa na oboch očiach. Endometrióza môže dôjsť na takmer akomkoľvek mieste v panvici. Redesign, inými slovami, zdá sa v mnohých prípadoch byť príznakom Michael Kors Peněženka propietor zmrštenie záujmu.
Abram je veľmi zdravá On je dobre vyzerajúci dieťa a interakciu s médiami v prípade, Aamir Khan povedal:" Nemám v úmysle vstúpiť. Snívanie o žlté znamená, že máte k dispozícii veľkú dôveru a budete robiť správnu voľbu v správny čas. Najhoršie zo všetkého nemôžem dostať, aby ma niekto veriť.
Ako by to zmenilo, ak by sme Ray Ban Brno boli to šťastie vidieť Ľan Bias rozvíjať na NBA súdu? Bias talent a popularita by veľmi pravdepodobne dali výrobnému odvetviu celkom novú dynamiku. Teraz by ste mali byť schopní prezerať a vyhľadávať na Play Store. Ako švajčiarska a juhoafrickej vlády by mali podporovať silný rozlíšenie na budúci mesiac zasadnutie Rady OSN pre ľudské práva v Ženeve, "povedal Keenan..
Kopula je oficiálne blízko v 07... Sme presvedčení, rozvíjať a postupovať v pravý čas so svojimi rád, návrhov a podporu predaja. Iste, je tu hlboký nesúhlas medzi lekárskej profesii o Lyme. Teraz sa vám to vedieť, či môžete predať! Potom máš všetky nové štítky šoku.
- http://youtoocando.com/?p=210#comments
- http://221.236.35.13/boke.asp?pmwkfndy.showtopic.103084.html
- http://xjxg.cn/thread-2036422-1-1.html
- http://bbs.massyw.com/home.php?mod=space&uid=33487&do=blog&quickforward=1&id=456344
- http://technowise360.snapbuzzz.com/activity/p/206082/
Nike Store Praha žiadny čas
Pri správnej etikety SEO môže vytvoriť webovú prezentáciu pre akékoľvek spoločnosti alebo podniku, ktorý je kľúčom k zaisteniu prevádzky od výskumných pracovníkov vzdelaných zákazníkov alebo záujem klientov.. Aj nehovoriac o moji chlapci prišli prečítaní vynikajúce užitočných tipov nájdete na svoje webové stránky a potom zrazu prišiel s hrozným pocitom, nikdy som poďakoval majiteľovi webových stránok pre ne.
To sa deje na úradníkov po celej krajine každý deň, že sú tam, aby nás v bezpečí, a vaše stanice sa dať do ešte väčšie nebezpečenstvo. Kreslenie na kádra skeptik vedcov, počas skorých a polovici roka 1990 GCC snažil zdôrazniť neistoty klimatických vedy a zaútočiť na matematické modely používané na projekte budúce zmeny klímy.
Efektívna komunikácia pre Vaše koncových užívateľov a stakeholdersFrom verejne obchodovaných veľkých spoločností, aby v súkromnom vlastníctve malé a stredné podniky, tisíce alebo dokonca milióny dolárov sa vynakladajú každoročne na trh. Rooney, obvinený z napadnutia urobiť, ublíženia na zdraví (s kovovými kĺbmi) sa pokračovalo až do dnešného rána.
Tu sú niektoré ďalšie veci, aby zvážila predovšetkým príbeh Jóba bol komfort pre mnoho veriacich v priebehu rokov. RIRI Nie je perfektné! Ale ona vie, ako sa cíti. Teraz si myslím, že o tom sa pohybujete na Nike Store Praha koľajniciach čoskoro! Eeep! Nike Boty Musíte byť tak nervózny, ako som bol späť v deň.
V deň, keď článok je publikovaný, nechal som sa trochu prirodzene organický prevádzku, aby to spôsob, ako sa na webe. Hovoril som sám pre seba:. Chceš predávať papierové učebnice? Fajn, ale radšej predať im lacnejšie než Laserové náklady na stránku.
Scan ak v poriadku, ale iba výstupy prázdnu stránku buď na tlačiarni náhľadu. Žiadny priestor, žiadny čas, len čistý nič. Aj keď je to dobrá voľba, ak máte veľkú informačný bulletin, to znižuje otvorenú rýchlosť svojho spravodajcu. Naším cieľom je slúžiť ako komunikačná platforma pre Latinskej Ameriky a záujemcov v Latinskej Amerike.
Naopak: Nedávna štúdia ukázala, že vymáhanie daňových zákonov uvoľnila v mesiacoch viesť až k voľbám, pretože zavedené si chcieť obťažovať voliča a prispievateľa. Čo je dobrá vec, vzhľadom na nepreberné množstvo živá hudba na počúvanie, filmovej náhľady a názory, sportscasts, hry na stiahnutie zadarmo a zástupy iných pásma sania Zábava K dispozícii je v ponuke.
Na druhej strane, takmer všetci Nike Free Run Dámské ľudia jednoducho kúpiť akékoľvek jednotky USB kedykoľvek potrebujú prenášať dáta. Čo tieto postavy sa predstavujú je široká osobnosti spektra. Získate plnú Brýle Oakle pozornosť od nášho trénera, ktorý vás naučí všetko o tvaroch tváre a typy obočia vhodných pre ne.
- http://ciarcr.org/spip.php?article310/
- http://vyqqgo.com/forum.php?mod=viewthread&tid=1378123
- http://verdamilio.net/tonio/spip.php?article1502/
- http://propdxb.com/activity/p/483851/
- http://qwgift.com/news/html/?4468.html
Brýle Oakle sú zodpovední
Či už máte záujem o Inuit kultúru, naše exotickej prírody, hojnosť unikátnych vonkajších dobrodružstvo príležitostí alebo iných činností, náš blog bude mať pre každého niečo! . Pozrite sa na 2.013 Spotreba paliva príručke pre odhadovanej hodnoty spotreby paliva prírodných zdrojov Kanady.
Mám Win XP Home počítača, ktorý potrebuje mať prístup k podielu na Windows Vista v káblovej sieti. [11] Moorovho energetickej komické vystúpenie ako Van Dyke postava manželky, začal vo veku 24 rokov (jedenásť rokov Van Dyke je junior), z ako herečka a jej podpis tesné capri nohavice veľmi populárne a stala sa medzinárodne slávny.
Sú naozaj predčil sa s hudbou a tónom. Dr Solomon A. Čo je považované za normálne a prijateľné, sa neustále mení. Taim má v súčasnej dobe na dvoch miestach, a navyše nákladiak. Možno som misremembering, ale ja si to nemyslím. Ceny v živých hudobných baroch sa väčšinou dvakrát tak vysoko počas doby, kedy mal prehrávanie hudby.
Pedikúra sú bezpečné počas tehotenstva. 5. Jo, a na začiatok to preč, som ešte dokončil svoj e matematiky úlohu príliš. Pinstripe trikot naozaj kričať "kancelárske oblečenie!", Kým flitrami a trompe l'oeil motýlik veľmi jasne, aby pre formálne trikote.
Tento druh z jedného predmetu, že každý je rád, "stačí vedieť príliš veľa o tom. Moje štúdium v zahraničí Firma má škrupinu webové stránky, ktoré vyzerá celkom dobre, ale je potrebné skopírovať a grafiky. Je to tiež viesť neskôr k populistickým Jharkhand oslobodzovacieho hnutia..
V Británii je veľmi odlišný od toho vo Francúzsku, ktorý, podľa poradia, je veľmi odlišná od Nemecka. Opýtajte sa svojho lekárnika, ktoré vám pomôžu vybrať vhodný liek proti bolesti pre vaše dieťa.. Brýle Oakle Nie je to zlé pre spoločnosť, Louis Vuitton Praha ktorá je iba osem rokov.
En el mismo Aeropuerto compramos un Rail Pass, por 68 (SE puede Pagar kon Tarjeta). Ak hľadáte niečo iné, alebo dokonca naozaj, ale naozaj iný, Zeno Clash II môže len slušať. Paul Scholes cieľom bolo absolútnu belter! Že hlavička bola naozaj presné.
Máme celkom veľa dobrých hercov a mierne sa líšia v ich maniere. Ani organizácie, anonymné stretnutia novinky ani neosobné výstrižková služba, kvalitné weblog sa vyznačuje hlasom svojho editora, a spojenie, ktoré redakcia s jeho alebo jej publikum. Povedal Michael Kors Peněženka mi, koľko zaplatil za svoj domov, citovať ohromné množstvo, ktorá robila moje oči choďte veľký.
"Ide predovšetkým o to, že tí, ktorí by sa dal pracovníkmi v nebezpečenstve, sú zodpovední," Merritt said.However, Merritt zdôrazňuje, že . To malo tú správnu konzistenciu, a mal pekný Ray Ban Praha pokovanie s celou cíceru v centre, niektoré kúsky petržlenu, posypeme paprikou a veľkorysé množstvo olivového oleja.
- http://www.azzeh4dev.sy/phpBB3/viewtopic.php?f=67&t=1564207
- http://www.ccpshipping.com/search/node/
- http://verdamilio.info/org/spip.php?article573/
- http://e.wz.cz/403.html
- http://gm015.com/forum.php?mod=viewthread&tid=11115
Ray Ban Sluneční Brýle 56 odišiel v tretej tretine
Váš lekár môže len komunikovať s pacientmi alebo zamestnancami, ktoré sú v súčasnej dobe vo svojej oblasti vplyvu, určený biele kružnice so stredom okolo vašej postavy. V súčasnej dobe je možné zakúpiť genericky. Naše systémy sú postavené na pohodlie dospelých, a nie nutne v prospech študentov..
Učenia. Na konci viac ako 1000 ľudí v hĺbke noci zatknutý, väčšina z nich.. Ak ste zdvorilý, nebudem suka. Nakoniec ste daný sami dostatok času po rozvode nájsť iný vážny vzťah? Už ste dňa dosť? To môže trvať jeden, pár, alebo až za niekoľko rokov úplne 'obnoviť' z rozvodu a nájsť nový, trvalý vážny vzťah..
V skutočnosti, viac ako pár Ázijské ženy moji priatelia dali sa na Ray Ban Sluneční Brýle ázijských mužov Louis Vuitton Bazar práve preto (a príliš krátka, hovoria), a začať skutočne loví muža 21. Pretože náš pobyt bol v offseason a krátkym ľavým piatok neskoro v noci a odletel v utorok popoludní vyradený náš plán urobiť malý ostrov poskakovanie a namiesto toho prilepené na Sao Miguel.
Ak by som mala manžela, pravdepodobne by som sa ho naučiť, vedľajšie účinky a udržať ich v tajnosti mne spôsobiť sám falošný Príznaky po celú dobu.. Tam je tiež nejaký laboratórny dôkaz za silné klinické dojem, že v určitých situáciách môže mať dosiahnuteľné koncentrácie askorbátu selektívny cytotoxický efekt na malígne bunky, pričom je neškodný pre normálne bunky, čo vedie k regresii rakoviny v zriedkavých prípadoch..
Keď Nichol len na tyči strelou na prestávku ďaleko s 1:56 odišiel v tretej tretine, Lapierre pokračoval skontrolovať Nichol do dosiek zozadu.. V tomto kurze budeme preskúmaná Lewins 'predstavy o organizačné zmeny, ktoré zahŕňajú' rozmrazovanie, pohyb, a zmrazenie ', ktorý má čo do činenia s pohybujúcou sa od súčasného stavu, učenie sa novému správaniu a posilnenie a udržanie nové správanie.
'Povedali Belstaff Praha sme si:' Prečo nie vytvoriť životný štýl okolo niečoho, čo máme radi robíte? ', 'povedal Nick. Najčastejšími dôvodmi pre to nemajú dostatok železa, pretože ste stratili krv (najmä ženy, ktoré majú ťažké obdobie), alebo preto, že je nedostatok železa vo vašej strave, ale existuje mnoho ďalších možných príčin..
Niektoré z nich sa môže byť dosiahnuté s insekticídom. Vzhľadom k tomu, zlá hygiena znižuje svoje lekárske zručnosti, budete chcieť, Brýle Ray Ban aby sa vaše ruky a telo v čistote. Naše Level Maths Tutor Brighton pochopiť, že dostať sa stupeň nie je len o memorovanie vzorcov; je to o uplatňovaní vedomostí a pochopenie problémov a konceptov niečo úplne iné, než len mechanické memorovanie..
Lietadlá môžu ešte pristáť a vzlietnuť, ak ešte vo fronte). Vegetariánska a non vegetariánska kuchyňa tohto mesta je inšpirovaný z najlepších domácich kuchýň z rôznych častí Indie. Tí, ktorí v očiach verejnosti vedia, že by mali pustiť túto tému, budú trpieť následkami.
- http://stannschoir.org/activity/p/442388/
- http://erlangga.co.id/forum/newtopic.html
- http://fzyhgd.com/news/html/?239150.html
- http://www.reo8.moe.go.th/index.php/forum/5/2576577-bryle-ray-ban-#2576577
- http://www.yuantianxiahj.com/news/html/?28248.html
Boty Ugg y
Päťročnice začal v roku 2012 13. Bývalý kardinál a súčasný pápež, ktorý, ako už bolo preukázané, dohliadol na to, že tisíce a tisíce maloletých by mohli znásilniť jeho kňazov, ktorí zostali bez trestu, pretože sa vzťahuje až zločinov na celom svete, a tým napomáhanie a navádzanie nových trestných činov, je až teraz nie je ohrozená s prípadnými sankciami.
Kay Henderson Des Moines, Boty Ugg Iowa (Reuters) Iowa dosiahla predbežné dohody s federálnymi úradníkmi na pláne na rozšírenie počtu obyvateľov s nízkymi príjmami štátu nárok na Medicaid pod vedením prezidenta Louis Vuitton Kabelky Baracka Obamu reformy zdravotníctva zákona, Iowa guvernér povedal vo štvrtok.
A to je dôvod, prečo sme vytvorili Batoľa čas, najmä pre tých najmenších! Zapíš sa každý utorok a štvrtok od 9:30 do 11 hodín a od 14:00 do 15:30. To sa líši od prílohu v tom, že je načítaný do databázy len raz so všetkými následnými odkazy na dokument (y) uložené ako odkazy.
Vstavané webové stránky pomocou takých nástrojov, ako CSS, HTML a jQuery. Miesto, s bezpečným prístupom, je teraz zjednodušená a jednoduchšiu navigáciu, hovorí de Boer, ktorý ponúka aktuality každý deň a priemysel výskum. Ten chlap nebol provokoval ako toľko miest, tvrdí.
Nedávne zmeny v Mexiku ekonomike naznačujú, že to môže byť aj konzervatívny odhad ... Mnoho druhov typoch prípadov a ochrany sa dostal nastavená tak, aby, keď potrebujete zabezpečiť malé a stredné zabezpečenie iPhone pri použití denne. Talianskej, mexickej, Američan, a viac sa upokojiť akékoľvek vyberavý jedlík, ako aj zabezpečiť Oakley Praha pre tých, ktorí sú ochotní skúsiť čokoľvek.
Namiesto toho to bol "otvorený bazár úplatky, protekcie a úplatky", ako New York Times vyjadril, vytvára viac než 10 miliárd dolárov nezákonných finančných prostriedkov na režim a miliardy viac na ruských a francúzskych politikov a podnikateľov Saddáma Husajna.
Je to nápoj AMT Coffee mali o svojich ponukách na dlhú dobu a ja som ho kúpil často na ceste do a z univerzity, ale Costa je sladšie a punchier, vyrobený s ovocným sirupom, skôr ako práškové paketu a obsahuje . Existuje mnoho ďalších faktorov, ktoré musia prísť do hry, akonáhle sa dostanete na návštevníka na vaše stránky: správ na odkazovanú stránku, ponuku, výziev k akcii, kvalitu grafiky, ceny výrobku (najmä pri porovnaní s inými weby .
1,2 m Prime Dôraz by mal byť v poriadku tu. Podľa Hollister Tepláky štúdie 2011, ALA tiež znižuje množstvo telesného tuku by liečenie cukrovky a vysokého krvného tlaku [6]. Ale to, čo som stratil, alebo nikdy, bolo to, že oblasť mozgu, kde materstvo prebýva ... Aljaška Radio Experimentálne Expedícia: To je to, čo hovorí Blue Sky: February 1940 Hubbard bol prijatý za člena Klubu prieskumníkov "v New Yorku (hoci jeden účet Scientológia hovorí 1936).
- http://victoryseller.com/news/html/?91802.html
- http://www.consegui.me/index.php?page=item&id=171986
- http://publicis.com.cn/forum.php?mod=viewthread&tid=426824
- http://www.ovnprod.com/spip.php?article33
- http://zejz.com/news/html/?65637.html
Moncler Outlet Online aby hodiny od ľudí
Iní môžu znovu pripnúť fotografie, čím sa šírenie dosah fotografiu na Pinterest. Obchodné bola zahájená "Steady" Eddie Stobart v roku 1950 ako poľnohospodárske podnikanie v grófstve Cumbria. Poznámka editora od Rebecca Snowden: V poslednej dobe, Institute of Medicine (IOM) vydala správu s názvom "zmiernenie bolesti v Amerike: Blueprint pre prevenciu Transformácia, starostlivosti, vzdelávania a výskumu", ktorý vyzýva k spoločenskú reformu v tom, chronická bolesť je podarilo, pretože to je národná kríza.
Okrem toho, že zábavné výpad na videohry humbuk priemyslu, je to tiež, myslím, celkom zdravý postoj pre videohry fanúšik vziať.. Výročie vydania. Namiesto toho, aby hodiny od ľudí, ktorí prestali na tých, ktorí majú len veľmi málo hodín (3 dni v mesiaci Moncler Outlet Online v niektorých prípadoch by mal byť čiastočný úväzok) hodiny sú uvedené na ľudí, môj šéf má rád prinútiť ich k práci 28 dní z .
Vo svojom zostavení môžete zvárané dosku na ňom objavia. Mohli by ste vytvoriť zoznam každého z všetkých vašich sociálnych sietí, ako je vaša stránke na Facebooku, Twitteri krmiva, alebo Barbour Bundy LinkedIn profil? Dobrý príspevok.. Umožňuje užívateľom vytvárať on line profily, hrať hry, preskúmať hudbu, chatovať, a ešte Oakley Cz oveľa viac; .
Tiež sme počuli chválu na Cinco de Mayo hamburger.. Natívne terénne bolo pochádzajú z okruhu 100 míľ obchodu, s cieľom zabezpečiť vhodnosť, a tam sú regenerované vody a ďalšie funkcie pre úsporu vody. Ale Barbour Praha posledný MRI ukazuje úspešne rozbalený chrbticu.
Stretol som svojho syna v Kalifornii, a potom sme leteli do Austrálie splniť náš tím. Tieto kontrolné dokument programy umožňujú právnici pracovať efektívnejšie a zároveň šetrí nesmierne množstvo priestoru, a preto náklady tým, že eliminuje potrebu objemné organizáciu papiera a zakladacej systémy..
Nakladanie s takými pochybnými on-line zdrojov, je istý výstrel spôsob, ako dostať napálil. Záver. To by mohlo byť nádherné miesto na doručovanie nahor. Môžete sa tiež pozrieť na fotky z rôznych typov bielych škvŕn na koži tým, že ide o Google obrázky.
Domorodé komunity boli nedostatočne pre mnoho vecí, ako sú kanalizácie, vzdelanie, slušné bývanie, dokonca aj veci, ako sú základné a podľa potreby aj vodou. Internet marketing sa nemôže odchýliť marketingu a reklamy prostredníctvom siete s internetovej stránky.
Vždy majte na pamäti, udržiavať profesionálny spôsob u všetkých riadenia. Dôvodom pre toto oneskorenie je dvojaký, jednak sme chceli zabezpečiť našim akcia bola postavená na robustnej údaje, a to je nutné nás analyzovať a zachytiť výsledky našej rovnosti Performance Hub.
- http://verdamilio.info/org/spip.php?article573/
- http://xigeart.topnic.net/forum/forum.php?mod=viewthread&tid=344107
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article5818/
- http://www.ibiker.cn/thread-1765806-1-1.html
- http://www.mariettakaramanli.fr/spip.php?article647/
Ray Ban Cz ale obranná jednotka
Som sa opýtať, či niekto, kto prijal Cymbalta a dostal nežiaduce sexuálne nežiaduce účinky, keď mal ich sexuálne nežiaduce účinky odznejú. Som muž v mojich 20s, a okrem nežiaducich účinkov liek funguje dobre. Beriem liek na kýlu v krku, a až neskôr zistil, že liek je tiež antidepresívum s potenciálnymi sexuálne vedľajšie účinky. Chcel by som počuť niektoré osobné historky / problémy / úspechy, ktoré sa zaoberajú sexuálny aspekt lieku. [Viac vnútri]
Čas sa dostanete loptu na obranu, keď sa pokúsite, že pristátie, povedal Wilson. len využil svojich chýb. bolo niekoľko z nich, ale obranná jednotka, ktorá bola ohováral a zranenia náchylnejšie produkoval jeden z jeho najlepších úsilie sezóny. Havrany boli len 5 za 14 pre tretie dole konverzií, a zlyhal na všetkých troch svojich štvrtý down pokusy, jeden príde vnútri Patriots 5yard riadok. Obraty a bránková čiara stáť? Na deň s pomerne nečakaným výsledkom, to dávalo zmysel.
Parklets Ray Ban Cz majú priniesť pocit rozmarne a spontánnosti, do mesta, ale aj napriek hlásenú investíciu vo výške $ 15.000 25.000 dolár za parklet, priestory našli niekoľko užívateľov v Bostone. Môžu byť príliš blízko k tradičnej parkov, alebo príliš Navrhnutie osobitnej. V Jamaica Plain, sa prehla lavice v jednom parklet ponúkajú väčšie dobrodružstvo skateboardistov, než pohodlie pre konverzáciu. Vineet Gupta, plánovanie ředitel Boston dopravné oddelenie, povedal Globe dúfa, že použitie týchto parklets zdvihne budúci rok na jar.
Príkladom toho je, keď spoločnosť, hovorí malý mobilný telefón spoločnosti, zahŕňa sankcie vo svojich zmluvách, ktoré vyžadujú dodatočné poplatky za zbierok omeškania. Obvykle pod štátnym Nike Boty právom, bude poplatky za neskoré mať nejaké čiapku a robiť ďalšie poplatky v súvislosti s touto platbou bude zobrazené ako súčasť neskoré poplatok. Spotrebiteľ nemôže vzdať týchto práv.
'Čo ponúkam je vážny plán pre vyrástla krajinu,' povedal delegátom. 'To bude vytvárať pracovné miesta. Majte hypotekárne sadzby na nízkej úrovni. Nechajte ľudí, aby viac ich dane z príjmu zadarmo. To je jediná cesta k lepšej životnej úrovni.' Konzervatívci boli nútení reagovať na sľubu práce na svojej vlastnej konferencii posledná týždeň, zmraziť účty za energie ľudí v prípade zvolenia, sľub, ktorý pomohol tlačiť svoj náskok v niektorých prieskumoch verejnej mienky z celej tri až 11 bodov.
Janis, na sebe ružové hodvábne minišaty a biele sieťované pančuchy, Longchamp Le Pliage toted zapečatenú fľašu Southern Comfort, jej ochranné známky úliatbu. To bolo prvýkrát, čo som usrkával Southern Comfort s Janis, nie menej! a išiel dole ako cukríky. Prvá Nike Roshe Run vec, ktorú som si všimol na rozdiel od svojich krepaté špinavé blond vlasy a nádherné bradavky strkať na šatách, boli malé krátery z detstva akné tváre bolo niečo nesmierne skutočný o dámu. Vyžarovala vôňu ženy, a nie len tak hocijakú ženu: prejdite na čerstvý bylinkový šampón z nej hustú hrivou, pot z podpazušia a snáď od medzi jej nohami, isté je ne sais quoi. Bola to všetko funky zmyselnosť. Jej silný těžkomyslný telo mäsité, ju stále posúva dcollet odhalil dokonalé melónu v tvare prsia a nohy, ostýchavo prekrížené, bolo snom. Jej přepjali Texan hovoriť ospalo bol obvinený tupým spovednice tónom, ktorý povedal: 'Počúvaj, ty radšej toto právo inak!'
- http://www.qqyyxx.com/forum.php?mod=viewthread&tid=351954&fromuid=34950
- http://www.yichun360.com/bbs/forum.php?mod=viewthread&tid=175749&fromuid=4242
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article5818/
- http://www.beijingsg.com/news/html/?78458.html
- http://mariettakaramanli.fr/spip.php?article705/
Ray Ban Sluneční Brýle Zynga sloty výrobky nie sú dobre.
Tým môžete vybudovať dôveru a vyhliadky čoskoro bude vaše Ray Ban Sluneční Brýle dlhodobé zákazníkov pre svoj online obchod. Guvernéra prešiel Meghan až Martinez než ten druhý muž spustil lano k nemu, a akonáhle bol hore, Martinez povedal mu, že by mohol prísť do ich tábora, ale tam boli dve pravidlá: Martinez bol v poplatku a bez vlastnej hmotnosti.
To stojí za zváženie, prečo developer sa chystá na crowdfunded trasu. Plánovanie tábor môže zdať skľučujúca, ale ak budete postupovať podľa týchto krokov, mali by ste mať pevnú štruktúru s ním pracovať. Pridanie urážku zranenia, Zynga sloty výrobky nie sú dobre.
Mojou úlohou je pomôcť chlapci zo všetkých oblastí života stretnúť so ženami, stavať príťažlivosť, a mať úspešnú datovania život. Toto pravidlo, Ugg Válenky ktorý bol schválený Fedu a ďalších agentúr, je zameraná na predchádzanie mnoho veľkých bánk z obchodovania vo svoj prospech v nádeji, že zabráni praktikám, ktoré pomohol viesť k vypuknutiu finančnej krízy 2008..
Stupeň je výzvou mnoho spôsobov. Ak študent má aspoň jednu kartu zo sady, oni si vyberú niekoho opýtať, čo máte? Ak osoba, sa pýtali má túto kartu, musí to dať ten, kto požiadal. Stačí urobiť niekoľko kôpok okolo mravcov trás a počas niekoľkých dní, vaše ant problémy sa doslova zmizne..
To ukazuje, horné vedenie, že vezmete jobseriously a chcú neustále zlepšovať.. Tá sa pohybuje od písania tlačových správ a hodnotenia, vytváranie a zostavovanie súťaže a rozhovory vysoký profil app vývojárov. V niektorých prípadoch, to je predĺžená do garáže a dvor na dvoch miestach, kde 'veci' má tendenciu sa hromadiť.
Tereza: 'No, ste práve urobil.' Skóre!. 'Mám Longchamp Cena rád, keď sa niekto v blízkosti pacienta je tam,' hovorí Ralph Brindisi, MD, klinický profesor medicíny na University of California v San Franciscu. Medové týždne David Moyes 's klubom sa tiež zdá byť u konca.
Mali byť lepšie vybavení neskôr riešiť tie dlhé písanie úloh. To sa vzťahuje na problémy pri vykonávaní dlhodobých plánov, stanovovaní cieľov a začatie krokov k dosiahnutiu cieľov. Som naozaj nadšený, vidieť, čo s tým robiť.'. To tiež znamená, že klient je šťastný a spokojný s vašou prácou, ale ak dostanete negatívnu spätnú väzbu od klienta, Michael Kors Peněženka nikdy si to negatívne.
Jeden z najviac uznávaných recenzovaných časopisoch v oblasti zdravia a životného prostredia, tento mesačník dôkladne skúma vedecký spojenie medzi zdravím a životným prostredím. Ale je jasné, že to nemohlo byť došlo bez jeho vedomia.. Jediný človek, s ktorým by mala byť konkurenčné voči sa sami.
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
- http://teecommunity.com/showthread.php?221577-Longchamp-Eshop-Ty-chce&p=222755#post222755
- http://lmusicradio.altervista.org/osclass/index.php?page=item&id=74614
- http://www.achicourtautrement.fr/spip.php?article451/
- http://bbs.dlhxw.com/forum.php?mod=viewthread&tid=685824&fromuid=35715
Barbour Bundy Je to film
Keby chceli vyzdvihnúť na Quvenzhan Wallis, mohli mať, ale oni by mali vedieť, kde bola čiara. Tento článok však hovorí Barbour Bundy niečo iné, zdá sa, že v pláne na ktoré majú viac "profesionálne" videa namiesto "hlavnej lode" videa. Ich dočasný charakter umožňuje prepínanie z rozmaru.
To znamená, že značná časť Ameriky sa dostáva jeho "novinky" od Topix. Je to zaujímavý zoznam, ale myslím, že si vybrali podivný výber pre číslo jedna: "mestská legenda" o President Woodrow Wilson údajne poznamenal, že ultra rasistické filmu Zrodenie národa bol ako "histórie písané s bleskom" a "všetky strašne pravdivé.
Intelektuálna nepoctivosť nepozná hraníc. Preslávil sa v knihách a filmoch, počítanie kariet je považovaný za podvádzanie, aspoň kasína. Novembra 2013 self opísal "hacktivist" Jeremey Hammond bol odsúdený na desať rokov vo federálnom väzení pre získavanie a zverejňovanie dôverných informácií zo súkromného obranná firma Strategic Forecasting (Stratfor).
Jeho filtrujú tiež objavil, že bol vyrovnaný. SlideShare je o prezentácie, Nike Boty prinášajúci snímky, dokumenty a videá obohatiť prezentáciu. Strávil som 12 dolárov na to. Planéta Zem je taký epos, že zarobí porovnaní s niektorými z najväčších hollywoodskych trhákov.
On je stále verí v hlavných generátorov tretích strán, ako je trilógia Enterprises Inc, Austin, Abercrombie Outlet Texas, ktoré sú dobré na hodnotenie šanca, že jedinec bude kúpiť vozidlo v rámci stanoveného obdobia. Mesto Memphis bol nachádza 28 km južne od modernej deň Káhira na ostrove na rieke Níl.
Je to film, ktorý by mal byť na zozname veľa ľudí filmoch. Existuje mnoho alternatívnych riešení, ktoré som nespomenul. Je to kompletné rodina rozvrhnutie, všetky tematicky konzistentné a vizuálne optimalizované pre platformu stránka je zobrazovaný na.
Ihly sú vložené buď po dobu niekoľkých sekúnd, alebo môže byť ponechaný na mieste o niečo dlhšie, v závislosti na požadovanom efekte. Bol som to šťastie pracovať s pánom Ramesh Tauran, Sajid Nadiadwala, Karan Johar, ktorí naozaj milujú svoje filmy. Recepty sú Tiramisu palacinky, grilované čiernu slivku a jicama šalát s čakanky, modré kukurica pizza s pestom grilovanými paradajkami a ricottou dedičstva.
HT Media taktiež vydáva Mint.The Tlačiarne (Mysore) Pvt. Je to úžasne hlúpy a suigenocidal. Neuveriteľné! Právnik obviňuje obeť za to, že expert. Budem blog si cestu Ralph Lauren Trička cez zvyšok Junior roka. Stanley Fischer bol technokratický 2 a vymáhač z týchto podmienok.
Bitka Burn App. Kamera ukazuje scénu temné kopca s mraky víriace okolo neho, zatiaľ čo Perry je vidieť jesť jahody, ktorý je symbolom slávy (to je tiež odkaz na svoj debutový album "One of the Boys", pretože disk má veľký jahodový potlačou na ňom), a steny blíži sa na ňu..
- http://retraitegenerationsacrifiee.fr/spip.php?article1173/
- http://ks35439.kimsufi.com/spip.php?article450/
- http://general.assembly.codesria.org/spip.php?article87&lang=pt/"/
- http://117.40.237.2/bbs/forum.php?mod=viewthread&tid=664566&fromuid=59502
- http://old.klafmann.com/index.php?option=com_kunena&view=post&do=new&Itemid=151
Ugg Válenky ale zdalo sa
Netreba dodávať, že Ráma nakoniec porazí démona kráľa a radostne sa stretol so svojou nevestou. Je to legrační, ma teraz, ale musel som to naozaj precízna presvedčenie, že striebro ani pracovať na mojej pleti. Snažím sa môj bestto prečítajte tam, kde mám voľný čas.
Potom som sa opýtal, aj ona môže aspoň jednoducho vrátiť a potom loď je na mňa tak, že nemusia platiť odpoveď:? Dobre, môžete ich vrátiť, ale potom budete musieť zaplatiť them.I reship potom . "Nemusíte mi fázy!" Jace povedal, keď unshifted. FastestChrome: Ako jeho meno by viedlo vás očakávať, FastestChrome pridáva niekoľko užitočných úsporu času nástroja na Chrome prehliadača.
Jedným zo spôsobov prepojenia budovy získal na sile v oblasti off page optimalizácie, pretože zmierňuje odkaz popularity a hodnotenie vyhľadávačov. Vezmite malé deti putt putt kurzy. Ďalšie cennou vlastnosťou je, že je možné obmedziť hľadanie na konkrétnu geografickej polohe.
Čo je to pohodlnejšie, než sa podáva jedlo s domáce varené kvality v jednom z Katy mnohých chutných reštaurácií? Mali by ste si rezervovať pre Da Vinci Ristorante Italiano. Ugg Válenky Miesto stimulácia, účinne zakázať nervové funkcie alebo zavedením nervový šum (.
Jeden skvelý tip pre použitie matné rúže sa pracovať trochu mimo strely s driekom z bavlny vatovým tampónom a potom zohrejte tým, že pracuje sa na zadnej strane ruky aplikovať štetcom. Myslím, že je to dôležité pre všetky z týchto prijímačov, tie mladšie, najmä (ktoré) sa uistite, že sú maľovanie na obrázok vpravo pre quarterback a učiť nuansy toho, čo robíme urážlivo.
Bez prognózy o tom, čo sa deje v ekonomike, možno budete chcieť držať sa svoje peniaze. Výsledky boli dosť podobné. False: Vaše prsia zväčší a môže zvýšiť v niekoľkých rozmeroch, po pôrode, Belstaff Bunda takže je logické, že sa cítite sexy svojimi curvier, perkier prsia, že Woolrich Jacket jo? Ale pravdou je, Louis Vuitton Peněženka hovorí myška, pravdepodobne ste vyhrali keď dojčenie je skvelé pre zdravie vášho dieťaťa, to asi nebude robiť veľa pre váš sexuálny život.
Než sme si mysleli, že je to elektrická sieť, ale zdalo sa, že všade okolo nás, a to nielen zo zdroja. Február Bay Area User Group (R programovací jazyk), sa konalo stretnutie s použitím RP hotelových zariadení. Ja čítal mnoho ďalších ľudí rád na túto tému, ale čím viac som čítal, tým viac si uvedomujem, že som nebol sám vo svojom hádať práce prakticky každý článok som čítal, je odhad niektorých kind.My hlavnej rady pre ľudí, ktorí chcú optimalizovať .
Ako zakladateľ Arianna Huffington vo všeobecnosti argumentovali, HuffPo poskytuje propagačnú hodnotu, ktorú poskytuje tým, že ponúka prispievateľom šancu byť vidieť na viac ako 20 miliónov unikátnych návštevníkov mesačne. Mike Pooley povedal pedicabs a rikša prívesy sú "v zásade považujú za motorové vozidlá" a riadi sa rovnakými právnymi predpismi.
- http://bidwindeals.com/blogs/viewstory/591075
- http://verdamilio.net/tonio/spip.php?article1502/
- http://www.027d.com/forum.php?mod=viewthread&tid=1564111&extra=
- http://francochilenos.com/spip.php?article594/
- http://0.0.0.0.ehhkzg.maxsc.org/bbs/home.php?mod=space&uid=467825
Barbour Bunda hovorí Northern Gateway
Fotografie sa objavili v médiách ukazovať Ram Charan stráže zbili duo ako ich prišla na spôsob, ako herca Aston Martin v nóbl Banjara Hills časti mesta. Médiá kritizovala policajný nečinnosť pri vybavovaní prípadu hovorí, že policajti nie sú pripravení zakročiť proti synovi únie ministra s nezávislým poplatku za ministerstvo cestovného ruchu.
Experimentoval Barbour Bunda som s ním; Čítal som návod, som si istý, že som vedel, ako moc o tom, ako som mohol. Urobil som nejaké chyby, zatiaľ čo robí tak, ale som sa naučil od jedného každého z nich. Som sa stal celkom zbehlý v nastavení príslušnej hodnotenia; pri čítaní učebných plánov a umiestnenie ďalšie kroky, na zdieľanie informácií so svojimi študentmi.
Strach zo mnohí z biblických proroctiev divákov a dokonca aj sekularizovaných svetových divákov ako Rush Limbaugh, Glenn Beck, a ďalšie je, že nadchádzajúce rokovania Kodaň a ďalšie im podobní predstavujú pokusy o globálnej elitári 'k vytvoreniu svetovej vlády. Zviera Antikrist a jeho falošný prorok príde z jedného svetového poriadku, podľa trinástej kapitole Zjavenia. Vývoj globálneho otepľovania krízy a volanie o globálnej správe, aby všetky národy sveta, aby sa veľa z ich zvrchovanosti je v popredí v súčasných novinových titulkov. Tak, to nie je príliš pritiahnuté za vlasy, vidieť, odkiaľ niečo cez vrchol vyhlásenie, ako je ten, nad príde.
Bohužiaľ, moja skúsenosť na oddelení urgentného príjmu je to, že Canada Goose Coat väčšina ľudí nemá hovoriť 'ona proste prišla, musím ísť.' Dosť bizarne, aj keď podľa všetkého myslí, že sú tu pre potenciálnych núdze, mnoho ľudí zostane na telefóne, keď som prišiel do miestnosti. Nemôžem vykonať zodpovedajúce históriu alebo fyzická s niekým, kto hovorí na telefóne. Môj prístup je, že budem čakať na chvíľu, a keď stále rozprávali, odídem. V ED, mám možnosť len vrátiť neskôr, keď mám čas (aj keď to môže byť za pol hodiny alebo hodinu neskôr, v závislosti na tom, ako obsadené sme). Lekári, ktorí vidia pacientmi na pláne nemajú taký luxus.
Autora: B. Weiner (1992) definované motivácia k učeniu ako o to, ako žiaci predstavujú pre svoje minulé úspechy či neúspechy. Študenti, Ugg Praha ktorí pripisujú ich úspech či neúspech stratégií intenzity alebo učenie, skôr než na ich vnímanie ich schopností, šťastie a / alebo obtiažnosti úlohy bude väčšia ochota učiť sa, a sa nevzdá ľahko.
Si mysleli, že sa jednalo o slam dunks,' Marc Lee, analytik na ľavej strane sa opiera Kanadské centrum pre politiku alternatívy, hovorí Northern Gateway, Keystone XL a ďalších projektov plynovodov súčasnosti čelí spoľahlivým odporom. Takže, čo sa stalo? Čo didn't.The potrubie Canada Goose Bunda bolo vždy bude čeliť ťažký boj na západ od Skalistých hôr v provincii, kde sa ekologické hnutie vzpruženie desaťročia starý 'Vojna v lese' proti starým rastu logging.Enbridge a oilpatch výrazne podceňovať sila Zelené Corp, starší, múdrejší a lepšie financovaná modernú verziu tohto spojenia farbené obyvatelia, ktorí boli zatknutí snažia zachrániť stromy v roku 1990.
- http://www.lzwenlian.com/bbs/forum.php?mod=viewthread&tid=976422&fromuid=53192
- http://verdamilio.net/tonio/spip.php?article1970/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article5818/
- http://s214.leosys.com/discuz/forum.php?mod=viewthread&tid=311183
- http://mariettakaramanli.fr/spip.php?article268/
Ray Ban Brno .
Helms pracoval v priemysle a akademickej obce na viac ako pätnásť rokov. Bol Ray Ban Brno som dosť dlho s RIM, že odpoveď na Vašu otázku by bola absolútne áno. Náhľad na zobrazený obrázok je spojená s pôvodným súborom. Tento druh vedomostí bude mať zásadný význam pri vytváraní istí, že ste jednoducho sú si vedomí najlepší spôsob, ako mať nezabudnuteľný nákupné skúsenosti.
Jednou zo skupín, ktoré je ľahko rozpoznateľné pre mňa je Univerzita v Utrechte klastra existujúce profesorov, doktorandov, študentov a bývalých kolegov. V skutočnosti, priemerný príjem je len asi 10 15 g na deň pre väčšinu z nás. Jednou z najdôležitejších častí je ich BBB (Better Business Bureau) Hodnotenie.
Kriminality v oblastiach, kde sú CCTV kamery v prevádzke dramaticky poklesla. Pieseň / video bol vyslaný, aby v pondelok večer. Pretože Japonsko je stiesnené, a obsahuje Belstaff Outlet mnoho prvkov odlišných typov a od rôznych generácií, len fotografovanie prirodzene vyústi v veľa nechcených a nepotrebných prvkov dostať do každej snímky.
Ak je váš článok editor je nafúknutý bordel, bude vaše ďalšie funkcie nezáleží. "Hoi pokračuje," tam je rozhodne vyzdvihnúť v kupca záujem zahraničných nehnuteľností v posledných mesiacoch. Niekedy domáce zvieratá sú kŕmené aj stolný jedlo ako drvič odpadkov: "zvyškami od stola Got Dajte im k zvieratám Budú jesť niečo?.!" Môžu sa deti učia pomáhať starať sa o domáce zvieratá? Okrem toho, len to, čo je tak zlé na tom, kŕmenie našich domácich maznáčikov ľuďom jedlo? .
Prostredníctvom série pozorovaní s ďalekohľadmi v Čile na Cerro Tololo Inter American Observatory (CTIO), Winkler a jeho tím, vrátane Middlebury College vysokoškolský študent Gaurav Gupta (teraz postgraduálne študent na Cornell University) a Knox Long z Space Telescope Science Institute v Baltimore, našiel slabú šupku žiariaceho vodíka obklopujúce miesto, kde sa hviezda explodovala.
Palin životopisec: "Myslím, že archívy Politicalgates sú najlepšie jediný dostupný zdroj pre každého, kto premýšľal, prečo otázky sú stále pýtal Sarah naozaj je Trig biologická matka." (Od 28.augusta 2011) Andrew Sullivan (Daily Dish): Politicalgates je "neoceniteľný" (od 28 februára 2012) Nike Free Run Prečítajte si Canada Goose Sale starý príspevok na Palingates o falošné tehotenstvo s obrázkami ešte neporušené v tlačenej HERE.Read staré príspevky na Palingates on-line HERE.We zlomiť "špirála mlčania" Prečítajte si podrobnosti o! "najväčší podvod v americkej politickej histórii" topánky na zemi v New Hampshire rally wit.America, máte na výber: Hlasujte pre čierne M .
- http://thehospoda.com/kunena/13-living-here/topic/create
- http://globaldialogue2013.go.tz/gdforum/activity
- http://www.suwentang.com.cn/bbs/home.php?mod=space&uid=86319
- http://general.assembly.codesria.org/spip.php?article87&lang=pt/
- http://www.sebalo.info/spip/spip.php?article11
Louis Vuitton Bazar Konca roka je zrejmé
Pamätám si, keď vám povedal, ako viac bozkávanie môže zachrániť vaše manželstvo? No, sme mysleli, že, ale tu pár, ktorý išiel trochu cez palubu. '. Vražda je závažné obvinenie. Tu vnútri panelu Vrstvy. Skôr, upgrade z fotografie HTC One ROM CyanogenMod nutné odomknutý bootloader, vlastné využitie, najnovšiu verziu CM a GAPPS.
Mám notebook, ktorý by som mohol priniesť, ale má 5 GB zadarmo len a ja by som radšej nechať doma. A podľa správ, on nariadil veliteľom minimalizovať civilné straty.. Každý rodič dieťaťa so špeciálnymi zdravotníckymi potrebami budú seba a svoje deti vidieť mnohokrát vo svojom čítaní tejto knihy.
To je priamy. Zväčšenie problémov prišiel znamenať, že 'pesimista' sa objaví znepokojený problému Aktívne sa zaoberá aktuálnym Louis Vuitton Bazar dianím vo svete; a dáva falošný pripojenie, ktoré kumulatívne úzkosť je získal trofej z nášho životného štýlu dnes. Rovnako uvádza, milióny mužov v Spojených štátoch trpí klinicky významnou poruchou príjmu potravy na niekedy vo svojom živote.
Konca roka je zrejmé, čas na opozičné strany, aby zoznam toho, čo oni vidia Air Max 90 ako zlyhanie Welsh vlády, ale dnes je aj pri PN hlasovaní o rozpočte práce. Celú pravdu o Business CoachingCoaching, všeobecne, je rastúci priemysel, do tej miery, že projekcie predvídať nedostatok trénerov v budúcnosti.
Priznala: .. Ste oprávnení na zobrazenie '+ +' metered_total_article_limit zadarmo články každých 30 dní, a v súčasnosti máte (% zostáva%) zostávajúce. Ja neviem, ako reagovať, keď sa ľudia gratulujem ma beh 26,2 mil. [22] [23] Zákon howevever, vetoval guvernér Oscar Mario Jorge ako jeden z jeho prvých krokov vlády, menej ako o tri týždne neskôr, s argumentom, že jeho nová interpretácia skorších právnych predpisov by mohla byť považovaná za protiústavnú.
Musíte si byť vedomí toho, že naši obchodníci sú povinní znášať náklady na riešenie spamu generované mail a tie isté náklady budú odpočítané z vášho účtu by mal byť náš obchodník sa uchýliť. Všetci vieme, že tam sú tony Moncler Bunda proteínových doplnkov, a asi v týchto dňoch, niektoré dobré a niektoré zlé.
Tieto malé čipy, aby stroj číta dokumenty jednoduchšie, ale mohol tiež, aby niekto so správnym typom skenera škriabať svoje informácie a sledovať svojho pobytu. Odporúčam požiadať o záväzok Prenajatý Názov politiky a získať titul poistenie, ktoré pokryje vaše nájomnej záujem, ak sa táto politika je k dispozícii v štáte, kde sa nehnuteľnosť nachádza.
Môj manžel a ja som zvyčajne ry robiť svoju vlastnú vec a snaží sa používať verejnú dopravu, keď v prístave, ale Haver Canada Goose Sale nikdy § Dva organizované výlety, ktoré stoja v mojej pamäti bol Iguazu Falls (môžete to urobiť pred nástupom loď) a Machu Pichu z Limy.
- http://www.francochilenos.com/spip.php?article1011/
- http://www.dailyqr.com/blog_entry.php?user=1297740&blogentry_id=25455314
- http://tancet-exam.com/forum/profile.php?id=90868
- http://www.jiese.cn/home.php?mod=space&uid=182748&do=blog&quickforward=1&id=9791951
- http://www.dailyqr.com/blog_entry.php?user=1336356&blogentry_id=25343607
Air Max 90 To je to
Nemusíte mať vedomosti, aby skutočne napísať článok ešte. Obliekanie na filmovú premiéru v novembri, Jenna otriasla po červenom koberci v mini farebné blokovaný šaty. Urobil tak v časti s trochou pomoci zvonku a čiastočne sa na topánky kožené kampane, že aj nedostatočne kampaň sa dá robiť (rovnako ako to urobil v Iowe).
Súhlasím s nimi prijateľnú úroveň nezávislosti, ktoré budú určite chcieť odísť na vlastnú päsť, takže je potrebné stanoviť základné pravidlá pred začiatkom dovolenky. Potom Inner City Press požiadal o sťažnosť, ktorá bola podaná s akreditáciou a spojovacie jednotky Louis Charbonneau, predsedníctva šéf OSN Reuters, ktorý používal bez kreditnej Inner City Press exkluzívny príbeh, ktorý americký úradník Jeffrey Feltman príde a práce pre Ban .
To vyhralo noviny roka za kalendárne roky 2007 a 2009 a je na Novom Zélande je tretí najvyšší v obehu noviny. Po štvrté, budeme radi, že sme rýchlo sa vzťahuje tento materiál po náš šiesty sneh deň zasiahne budúci rok. Phil Mickelson je robiť svoju tretiu kariéru začať v akcii a prvý od roku 2009.
Nemá to sa zdá byť ťažká úloha, ako sa ukazuje potenciál k rastu. Ale pomocou GPU, aj kefa z niekoľkých tisíc obrazových bodov na obrovský obraz je úplne Air Max 90 (ehm) tekutiny, reagovať v reálnom čase na ťahy štetca s perom a myšou. Roztomilý dievčatko, ktorá hrala v južnej Wild bol ťažký témou rozhovoru, pretože najmladší kandidát na hlavnú rolu v histórii, jej krásne meno je sústo a ona dokonale drzý.
Zavolal kamióny "na obtiaž," a povedal, že predstavuje "nekalej konkurencie", do polovice Wilshire reštaurácií v "stacionárne, povolených miestach." On pokračoval o tom, že potraviny nákladné autá by sa držať slúžiť stavenisko, kde zamestnanci nemajú ľahký prístup k inej potraviny, a že "by mala Abercrombie Mikina byť ich jediným miestom v meste.".
Je to štípe sakra veľa. 4. Palmer si myslel, že bude pracovať v záchrannej službe zvierat, a nakoniec otvoriť svoje vlastné dobré životné podmienky zvierat agency.16 bola prijatá na vysokú školu študovať učenie a bral kurz na žurnalistiku, ale vždy sníval o tom, acting.317 Palmer opustil univerzitu, aby .
To je to, čo som sa na prvom mieste.. Mnohí zákonodarcovia tlačí, aby túto sumu zvýšiť na 10 miliárd dolárov, aby poskytla viac podnet k firmám, ktoré by mohli byť odmietavý mechanických problémov, ktoré stoja viac k náprave, ako náklady na čistenie..
Dva príklady by to byť Americká akadémia fyzikálne medicíny a rehabilitácie . Trh trvalo ďalších päť viac rokov začať Nike Air Max 90 klesať v hodnote. Takže kanál svojich čitateľov, keď si klásť otázky. Prečo by ste si mali vybrať Belstaff Bunda replika Oakley slnečné okuliare? Tam sú skvelé ponuky popisov prečo.
- http://www.observatoiredesreligions.fr/spip.php?article11
- http://team-atomic.net/forum/viewtopic.php?pid=134006#p134006
- http://www.rmnx.com/docs/index.php?title=User:Tbnljrlr#Nike_Cz_Shop__83
- http://general.assembly.codesria.org/spip.php?article87&lang=pt/"/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article15378/
Belstaff Sherlock Coat srdce astronauti explodujú
GREENSBORO Bývalý Guilford County rada komisárov predseda Melvin 'Preskočiť' Alston oficiálne oznámi svoj boj o sedadlo Valného zhromaždenia v stredu. Popp, ktorý nahradil vystrelil Dan Hawkins päť hier do sezóny 2013, zostal neoblomný PPL, bola dosť dobré vyhrať šampionát.
Z väčších kusov šperkov, ja používam porcelán papier íl, ktorý má ľan miešať sa do neho. Namiesto použitia, že môžete experimentovať s rôznymi tvarmi. Dlhuje 253844 dolárov na jej hypotéky, úverové línie, auto úver a kreditné karty. Zamilujú sa do seba, ale Jeff má problémy jeho vlastné.
SAMPLE. 'Niektorí ľudia hovorili, srdce astronauti explodujú, alebo že ich krvný tlak sa zníži na nič. Myslím si, že v prípade, že softvér je tak optimalizovaný pre hardvér potom to beží 'meškanie' zadarmo. Videl, že ona bola 'ťahúň', a že mu dôvod, prečo sa s ňou oženiť, alebo tak jeho príbeh pokračuje..
Možno, horolezectvo. Riziko prasknutia aneuryzmou zvyšuje, ako aneuryzma dostane väčší. Októbra, ťažký armádne ostreľovanie rebela držal kurdskej mesto Tell Aran vľavo 21 civilistov. Nech už je dôvod pre nedostatok spánku, výskum ukázal, že Belstaff Sherlock Coat to berie daň na nás ako psychicky, tak fyzicky.
Ale hráči sú veľká pomoc.. / Ale ja som chodiť na rozbité sklo / len držať istom zmysle svoje vlastné istoty. Proti vysokému krvnému tlaku lieky som bol na, na druhej strane, mi jednoducho vyrazila Nemám tušenie, či to robilo niečo vedľajších účinkov; úprimne, musel som prestať brať to kvôli 'zaklopal ma' bit.
Nemáte niečo pridať, aby bol šťastný; musíš niečo klesnúť. Longchamp Cena Dvojica háčikov tyčí rozširuje smerom von od vonkajšieho konca zostavy priečky pre podporu jednej alebo dvoch bicyklov. Taborn má jazzové klavírne trio tradície do nového územia s deviatimi provokatívne kompozície, na ktoré Cleaver a Morgan presahujú úlohu podpornú rytmikou hrať rovnejšie úlohu v utváraní melódie a harmónie.
Vykonané na prácu s ministerstvom Hollister Tepláky zdravotníctva s cieľom uľahčiť nový výrobok na trh. Máme tendenciu preceňovať vplyv technológie v krátkodobom horizonte, a podceňovať vplyv technológie v dlhodobom horizonte. [10] Bez ohľadu na to, iracký futbal už nikdy nebude rovnaký.
Ústava skúšobného gramotnosť jazyka. Okrem toho, askorbát podával v farmakologických dávkach zvyšuje množstvo parametrov imunitnej odpovede na úrovniach vysoko nad trochu svojvoľné 'normálny' rozsah, vrátane buniek sprostredkovanej imunity a endogénnu produkciu interferónu.
Musíte mať na pamäti, že pred 2 mesiacmi nikto z prítomných povstania v severnej Afrike a v Perzskom zálive boli novinky. Pani Bolgiano má magisterský titul v odbore obchodná administratíva, rovnako ako Belstaff Bunda v bakalárskom študijnom programe, z Cornell University.Steven CaffeDr.
- http://www.guandongshan.com/forum.php?mod=viewthread&tid=1139219
- http://indogermanschool.org/2015/12/how-exactly-to-recognise-the-outward-symptoms-of-genital-herpes/
- http://www.ovnprod.com/spip.php?article8
- http://bbs.fjsszs.com/forum.php?mod=viewthread&tid=1108594
- http://www.lymldqx.com/forum.php?mod=viewthread&tid=155834
Canada Goose Praha sme sa dohodli na niekoľkých položiek
Caf sa nachádza v to, čo bolo pôvodne skladisko město vlak. Tu je návod, ako niektorí muži manažéri sú nápadné správne noty s kolegyne a spotrebiteľov. V prípadoch, keď sú informácie zaslané na tretiu stranu, vám bude oznámené Canada Goose Praha tretej osobe používaný, a musia mať možnosť odmietnuť z odovzdania, ak si vyberiete.
2) Nemôžem už dokonca začať hru. Ochranný Oracle laminované chráni pokožku pred opotrebením a zároveň dodáva ďalšiu ochrannú vrstvu pre device.At 0,01 mm Abercrombie Praha na výšku, MusicSkins pridať takmer nulové väčšinu, takže váš prístroj bude stále perfektne integrovať s takmer vo všetkých prípadoch, tašky, doky, iTrips, alebo náramky..
Putin tesnenie Hefty Pokuty za "Protestné činov" v Rusku. Po prvé, neti hrniec Nike Boty s práve teplou slanou vodou je výborným liekom pre každú nosovej kongescie, či už je to začínajúcich alebo pokročilých. Týmto spôsobom by regulačné orgány vedieť, kto je crowdfunding, ktorý podporuje ich a koľko raised.Social médiá by presadiť integrityAnd najdôležitejšie sociálne médiá by sa riadiť proces.
Flash pamäť používa pre čítanie a ukladanie do vyrovnávacej pamäte je MLC flash pamäť, ktorá je bežná v SSD a iných spotrebných výrobkov flash pamäte. Vzhľadom k tomu, ružová je ich preferovaným paleta, sme sa dohodli na niekoľkých položiek, z tohtoročnej sezóny hviezdou prehliadky kolekcie, ktorá sa vyznačuje hviezdy trblietavé zlaté, ružové, bohaté hnedej a krémovej farby.
Máme dobrú správu pre všetkých záujemcov o BSHB Recruitment 2013, 01 2013 141 (sto štyridsať jedna) voľné miesta v tejto doske, inzerát už oznámil, prečítajte si nasledujúce . Začnite s nízkou hmotnosťou, aj keď si myslíte, že môžete urobiť viac, takže don nadmernou telesnou seba a potom, ako sa dostanete pohyby nadol môžete postupne zvyšovať, ako sa cítite pohodlne.
Jeden z jej najlepších poviedok, "Bliss", slúži ako hlavné príklady týchto definujúcich vlastností. Za pár mesiacov som išiel webové stránky, webové stránky, aby sa uistil, že som preč z nich. Bol som spal lepšie, rovnako. Potom Zaujímalo by ma, prečo bol email údajne poslal z jedného "Stephen Massey".
Existuje Longchamp Cena mnoho ďalších otázok, ktoré sa vyžaduje úplné zverejnenie, ktoré vyžadujú pozornosť. Foot kluby by mohli tráviť viac času poradenstvo hráčov využívať sociálne médiá zodpovedne, skôr než grganie senior hráčov z vyjadrení ich považované za priamy a názory.
Nehnuteľný vynikajúci vizuálnu príťažlivosť na tejto stránke, sa mi to 10 10 Pomer Everyday Health je predná digitálny zdravie a wellness spoločnosť .. Počas nášho pobytu sa childeren chceli využiť bazén po prehľadaní všetkých papierovanie som nemohol nájsť otváracej doby bazéna, pretože sme nikdy nemali žiadnu uvítací balíček, tak sa obrátil s plávať krúžkami v 9 hodín ráno len aby povedal svoje majiteľa len do 10.
- http://www.beijingsg.com/news/html/?78010.html
- http://ciarcr.org/spip.php?article310/
- http://www.chat.nsqkl.org/viewthread.php?tid=1193827&extra=page%3D1&frombbs=1
- http://dedi.bargainspy.co.uk/user
- http://comcom-10.com/forum.php?mod=viewthread&tid=5931831
Canada Goose Bunda sú tam niektorí odborníci
Myslím, že Atom bude v poriadku pre mnoho základných potrieb ľudí, ale to je GPU treťou stranou na Clover Trail. Ale keď Aktuality Ltd Ľudia, ktorí vlastnia publikovať obvinenia identifikačné vnímanej korupcie, majú nárok na toľko slobody prejavu ako právo nás všetkých v súčasnej dobe umožňuje.
Read ReviewThe Civic je k dispozícii s dvoma Canada Goose Bunda benzínovými motormi, ale je to 2,2 litrový motor i CTDi diesel to je náš obľúbený. "Je to ako posledná kvapka. Stráviť trochu dlhšie dokumentácie a pripomienok, ako by ste mohli robiť normálne, a naozaj sa snažia premýšľať o tom, čo niekto čítaní by sa mohli pokúsiť sa objaviť.
Máte tušenie, čo je skutočné alebo falošné. Neskôr Leanne presvedčil svojich rodičov, aby ho spustiť ako podnikanie. Indická meď Ter ms vlastného priemyselného posúdenie minerálne, India má nedostatok medenej rudy ako prírodného zdroja. Cena je 70,00 dolárov pre dospelých 50,00 dolárov za dieťa / Ray Ban Brno seniorov.
Znovu založiť na výrobných faktoroch, ako je napríklad dopytu a ponuky, keď je dobrý zdroj, každý národ by mal dať prednosť zabezpečenie zachovanie toho, čo má, a to je, keď dopyt je nízka. To hovorí, že pôda nie je beží dobre, a sľubuje, že vyhrať slobodu pre ľudí tejto krajiny.
Rozložená na 56 ha, to bolo dokončené v roku 2002. Ale ich výzva pre územnú blízkosti je len výhovorka, aby sa zabránilo rokovaní. Je tam otázky, ktoré nemožno odpovedali áno, sú tam niektorí odborníci, ktoré nie sú tak veľké ÁNO. Našiel som počítač a dostal všetky súbory, Air Max 90 Hyperfuse potom sa deje okolo plnkou veci z domu do veľkého čierneho vreca som si so sebou, keď som náhodou narazil na preteky a nastavenie alarmu.
Google vám zasielanie ton prevádzky zadarmo, ale to nestačí, takže sa nákup reklamy na Google. Ak ste Dennisa Ryder a nechcete, aby Michael Kors Praha váš obrázok, ktorý bude zobrazený na 123people, prosím odstrániť obrázok z pôvodného zdroja. Gepard (Acinonyx jubatus) je veľký mačací (rodina Felidae, podčeľaď Felinae) obývajúce väčšinu Afriky a časti Stredného východu.
Ja som si všimol, že to nie je len hlavný index stránky, ktoré môžu byť ovplyvnené tým mám niekoľko mini webov v rámci rovnakej lokalite, ktoré boli zasiahnuté tiež. Ríša bola vždy mestečko operácie. Je to cieľ zdravých rodín a zdravých komunít. Vždy som sa smiať, trochu, keď počujem ľudí hovoriť o ostrove rovnakým spôsobom hovorí o legitímne Detroit krachu.
V skutočnosti, monitorovacie stanice Národný park Rocky Mountain, ktoré merajú, ako Thompson River Big bude dariť tento rok na jar a v lete ponúkajú niektoré štátne najhoršie správy. "Je to ako posledná kvapka.. Street na pešej zóne v St Mary obsahuje obchody so starožitnosťami, darčekové obchody, nezávislé kníhkupectvá, kaviarne a reštaurácie.
- http://lellovoce.altervista.org/spip.php?article412/
- http://www.shanghaisoft.cn/bbs/forum.php?mod=viewthread&tid=1070764&extra=
- http://szhdad.com/thread-55025-1-1.html
- http://tianjin.xn--fiqs8sx3j.com/bbs/home.php?mod=space&uid=405920
- http://www.francochilenos.com/spip.php?article1011/
Nike Store Praha Dát je tiež tak šikovný
Všetky tvrdá práca je zrazu fuč a človek nájde sám znovu fajčiť uspokojiť nikotínu opice stále na chrbte. To, že tendencia skĺznuť späť do fajčenia, ktorý umožňuje dostať prestať fajčiť pomoc, ktorá rieši príčinu fajčenia tak dôležité. Prvým cieľom je pochopiť, triggery, ktoré spôsobujú chuť k prepätiu. To vám pomôže buď sa im vyhnúť, alebo aspoň byť pripravení ich napadnúť, keď dorazí.
Návrate bol ten rozdiel, že Rancocas Valley tréner Anthony Corrado. Nemáme mať Kristin pravdepodobne prehráme. Musíš ju spustiť s autom, aby ju z hry, to zviera. Hrala fyzickej, beží na podlahu tak aj pre veľké dievča a boli sme schopní ju nájsť pre niektoré veľké body. uzavreté Rancocas Valley bod za bodom a skočil na 20 17 vedenie po Brielle Mattiello Nike Store Praha skóroval po sebe idúcich bodov uzavrieť v prvom štvrťroku. Hybnosť nasledoval na druhom štvrťroku Julia McClure, ktorý skončil s 15 bodmi a 10 doskokmi, prevýšený v po sebe idúcich laických up Air Max zažať Ralph Lauren Praha 14 6 beh, že Alyson Toman, Belstaff Bunda ktorý viedol s kariéru vysoké 17 bodov, zavŕšený sa chrbtom k sebe skóre nízko. Beh povolený Hudson County škola vziať 34 24 olovo, jeho najväčší z hry.
Dát je tiež tak šikovný, tak dobrý, ako softvér, ktorý zlepšil svojej práci. Inými slovami, stupeň inteligencie údajov bude čiastočne závisieť na kvalite softvéru. Že v dopadoch otočte efektívnosť výsledného inteligentnej právnej údajov do vlakov nové dáta pri vstupe do systému. Rovnako tak by sa ďalšie prvky, ako je rozmanitosť alebo rozlišovacej spôsobilosti predchádzajúcu alebo ďalšie údaje.
QMI Oil System Cleaner cirkuluje motorom, kde jeho koncentrovaný olej na báze detergent akcie drhne preč ďasien, lak a karbónové usadeniny. Potom suspenzné činidlá emulgovať nečistoty a znečisťuje pre bezpečné vybratie z kľukovej skrine na oleje drain.Helps znižuje spotrebu oleja zo zakázaných alebo blokovaných návrate výmeny oleja kanály v hlave valcov. Ak tomu tak nie je riešená, je táto podmienka prispieva k ochudobneniu dodávky oleja a seizure.Helps motora voľných lepkavých zdviháky a udržiava dobré prúdenie mazivá skrz engine.Frees piestnych krúžkov pozemných vkladov, čo znižuje stratu kompresie a vyhodiť by.Extreme tlaku agenti zlepšenie mazania kritických oblastiach a ochranu proti strate mazania pri cleaning.Helps predĺžiť životnosť motora odstránením abrazívne častice opotrebenie kovových a nečistoty, čo znižuje opotrebenie motora pracovných prvkov, tesnenia a O-krúžky.
Amnesty International povedal, že uvoľnenie dokumentov bolo vítané, ale odsúdil rozhodnutie zablokovať stíhania. Vlastný odhad generálny prokurátor Eric Holder je, bol zapojený do mučenie, 'povedal výkonný riaditeľ Larry Cox.' Žiadny civilizovaný definícia 'primeranej' správanie môže niekedy zahŕňať mučenia. Mučenie je už dlho uznávaná za porušenia národnej i medzinárodného práva, a nie jeden právny názor, bez ohľadu na to, z akého zdroja, to nemôže zmeniť. '
- http://www.snesup-paris13.org/spip.php?article16/
- http://pcbbbs.net/read.php?tid=468/read.php?tid=468
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
- http://verdamilio.net/tonio/spip.php?article1739/
- http://mtgcyprus.com/index.php?option=com_kunena&view=topic&catid=6&id=201566&Itemid=77&lang=en#207712
Nike Air Max zubár je niečo
Hovoril, Nike Air Max že prišiel z JUCO, možno nedostal všetky nesie vo svojom prvom roku na Havaji. Nesmiete použiť proxy server. Definícia Žena Cougar voľných starších žien datovania lokalít, 60 rokov starý Cougar Cougar femmes stretnutie Cougars on-line hot miestnej pumy muž datovania staršie ženy Pumy dvojhry Ray Ban Praha mužov, ktorí radi staršie ženy staršie ženy datovania mladších mužov stránky mladá žena verí v prednej webe za stránok uvedomujú
Pokiaľ založená v pohotovostnom režime, využíva púhych 0,07 wattov. Táto stratégia je stále vo svojej Ugg Praha experimentálnej fázy a napájacie jednotky sú aplikované na oboch školských autobusov a Charty autobusy rovnako. Neschopnosť mesta k udržaniu dostatočne personálne policajné oddelenie, jeho nedostatok predvídavosti pre kompenzáciu opotrebenie a jej pomýlené posadnutosti nonpunitive anticrime programy zhoršili problém, ktorý v žiadnom inom meste by sa dal opísať ako kríza len ..
Vyliezol na mňa, som skôr prísne ho informoval, že ja som chcel mať sex s ním. To len negatívne. Ak budete tráviť peniaze na kúpu tú prekliatu vec, ktorú by ste zaplatili okolo 300 dolárov, a ešte zaplatiť takmer 40 dolárov za mesiac. Kategórie. Avšak, aby bolo zaistené, že jednáte s stojí za spoľahlivé agentúry, budete musieť urobiť dobrý výskum na to.
Tábor mal AOL dial-up, potom satelit, a teraz širokopásmové pripojenie. To je kratšia beh rozhodla som sa prejsť na vode. Vidíte, zubár Belstaff Sherlock Coat je niečo, čo by ste naozaj nemali prepínať z jedného do druhého, ak nemáte naozaj dobrý dôvod. Teraz je potrebné pridať tento hodnoty / text 's do skrytého vstupu, ktorý bude vybudovať reťazec ako je uvedené vyššie všetkých užívateľov výberov, to potom bude pridaný do mojej databázy do poľa s názvom "vlastnosti" (ja viem, ako to urobiť dátová časť bez pomoci tu potreba, stačí vám na tom, ako pridať hodnoty do skrytého vstupu)
Nesené currentsThen, v roku 2008, obrovská populácie bol nájdený v juhovýchodnej časti jazera. Nehovor Love slovo. Oni veria, že to bude oveľa bezpečnejšie a praktickejšie. Existuje veľa vecí, ktoré som naozaj rád o ňom (prehliadača a skvelé apps aby sme vymenovali dve), ale tam sú veci, ktoré som don ako toľko ako ako nedostatok volanie / koncových tlačidiel pre jedného.
Dokonca aj váš uvítací stránka by mala byť názvom niečo dôležité pre vaše webové stránky. Ak tak urobíte obdržíte County Court Predvolanie z DVLA o kontinuálne registrácii, pretože ste nedostali potvrdzovací list, ale ste presvedčení, že ste poslali podpísanú časť registračného dokumentu a mať kópiu ako doklad, môžete sa rozhodnúť ísť na
- http://www.francochilenos.com/spip.php?article2750/
- http://sippe-onyx.de/index.php?page=Thread&threadID=454264
- http://www.jngi.org/forum/profile/utyrcese
- http://verdamilio.net/tonio/spip.php?article1739/
- http://www.promo-grimpe.com/spip.php?article124/
Nike E Shop domov Dinky dinosaurov
Nielen, že budete tiež môcť sledovať odkazy si môžete prečítať obsah, ktorý obklopuje obrázky môžete narazili "?" skvelý spôsob, ako readup na autá, ktoré ste hľadali Nike E Shop obrázky .. Ako sa hovorí, že na svojich internetových stránkach, ",,," PPC tréner je pay per click marketing fórum, ktoré Abercrombie Praha ponúka všetky vzdelávania, nástrojov, spoločenstvo, a 1on1
Zásadný pitnej vody doplniť naše telo veľkým množstvom tekutiny, ktorá môže očistiť náš systém nemožno dostatočne zdôrazniť dobre. A potom som strávila týždne po týždňoch svojho času sa snaží používať tie nástroje nič z to fungovalo .. Rusdenes pracuje v diskusných skupinách a fórach Spoločenstva, ale to je Pomoc a podpora fórum obývaný Zákazníci, ktorí dobrovoľne venujú svoj čas pomôcť ostatným zákazníkom
Ale on nemá môj rešpekt. V rozhovore s The Escapist, Sawyer Moncler Cz a iné predvádzal rôzne v herných miest, vrátane "miest Good Springs, Primm, Novák (domov Dinky dinosaurov), super mutantný ležanie na Čiernu horu, vojenské / vedecké Inštalácia Helios 1, Camp McCarran, pozemok RealWorld letisko Las Vegas a samotné mesto New Vegas. "
Republikánsky zástupca je nasledovníkom neoConfederate Ligy juhu .. Teraz on-line na zákazku na mieru tvorcovia košele ponúka mužom navrhnúť tričká podľa vlastného výberu, zatiaľ čo sedia doma pri ich jednoduché. Nie je mi to "podvod" povedal len, že to môže byť trochu selfcontained, alebo "márnosť agentúra", alebo možno jej skutočný hľadanie talent, ale to financuje sama tým, že nechá veľa ľudí, ktorí platia za udalosť, ktorá činí to vyzerá veľká a efektné, ale väčšina z nich jo dostaneš veľa z toho.
St Paul bol absolútne presvedčený o tom: "v Kristovi všetky veci na nebi a na zemi sú zmierení", napísal. Obchodníci dnes zriedka používajú hrubé mechanizmy, ako napríklad blikajúce slová na obrazovke. Ešte lepšia bola služba na recepcii. Brees hodil pre 307 yardov a štyri povolenia pristátie, posledný 9yd úder do Darren Sproles, že nastavíte záznam s 02:51 ísť.
Stále mám pocit, ako by to bolo dobré, aby sa hore, haha. To je, keď som si uvedomil, že zoznamka Afroromance môže byť tiež riešením pre moje rušný životný štýl, ktorý nemá časový interval pre datovania .. Zákazníci privítal novú politiku sa zmesou humoru, empatie, sklamanie, a viac ako niekoľko komentárov
Aj s HD 7950 pretaktujú, nemôže úplne dostať až na GTX 670 úroveň výkonnosti v tejto hre. Candace a ja musel vybojovať, že priestor bez prospechu, že sú Ray Ban Wayfarer spolu na cestách a chodníkoch. ASIGroup poskytuje informácie o všetkých typoch Trh cenných papierov obchodovanie, vrátane akcií, CFD, futures, futures a opcií ..
- <a href="http://general.assembly.codesria.org/spip.php?article87&lang=pt/\"/\"+target=\"_blank/" target="_blank">http://general.assembly.codesria.org/spip.php?article87&lang=pt/\"/\"+target=\"_blank/</a>
- http://steenburger.com/search/node/
- http://bbs.go19.cn/forum.php?mod=viewthread&tid=2670765
- http://www.general.assembly.codesria.org/spip.php?article87&lang=fr/
- http://www.onchoice.in/index.php?page=item&id=611815
Abercrombie Mikina samozrejme
[2] Kadidlo svieti pred oltárom denne, a ponuky, ako sú obľúbené potraviny, nápoje a 'duch peniaze' sú uvedené bi mesačne. Rozhodnutie o výbere systému pre riadenie výučby môžu byť na rade kritérií, vrátane pedagogických otázok, flexibilitu a jednoduchosť použitia a licencovania a prevádzkové náklady.
Nie že by to fandenie. Som bol vo veľmi násilnom vzťahu, ale nakoniec nechal som teraz exboyfriend. Kurníku s veľkým horských bicyklov rám a niektoré časti BMX môže vám ísť. V pláne zostať týždeň, 2 osoby + dieťa. Na Deň dôchodcov v konferenčnej sále vlády Circuit House, ShahiBaug, Ahmedabad diskutovať o aktuálne dianie a rôzne predmety týkajúce sa dôchodcov.
Bol veľmi Abercrombie Mikina rovné. Sa naučil z tohto prípadu:. Má nielen produkt bol skvelý, ale podpora bola skvelá rovnako. Alamo tiež slúži ako oficiálny prenajať auto Walt Disney World Resort a Disneyland Resort.. Ale budú potrebovať pas. Schopnosť interakcie s hudbou v prostredí virtuálneho sveta a bude avatara, Canada Goose Sale ktorý môže v reálnom svete robiť veci, snáď to nie je možné, môže byť veľmi vzrušujúce a motivujúce a môže byť zvýšená na Moncler Bunda hudobné vzdelávanie v inovatívnym spôsobom, ktoré neboli ako doteraz plne preskúmané..
Martha Mullet povedala, že si myslí, že vláda sa snaží rozdeliť komunitu, ale členovia sú odhodlaní zabezpečiť prežitie separatistickej skupiny, jej manžel založil. Zle platené a zle umiestnený, oni žili v 'nebezpečných nezdravých podmienok a promiskuity,' podľa novín časov.
Francúzsko, Španielsko, Nemecko, Taliansko, atď). Je dôležité, aby tam snaha definovať naše systémy viery skrze vedomé, racionálne myslenie a logické uvažovanie. Zavolal mi a povedal, že by bol doma 22:30,' povedala Anita. A množstvo váhy každý jednotlivec stratí bude závisieť od ich veku, hmotnosti a výšky.
V niektorých častiach Afriky, najmä Mauritánie a Maroka, obchod prisťahovalcov do Európy sa stala lukratívnejšie ako obchod s drogami. Tie krajiny, ktoré musia byť finančne vypomohol vždy postrádal vysoko kvalifikovanej populácie, ktorá priťahuje zahraničné investície a významných priemyselných odvetví, ktoré môžu súťažiť na svetovom trhu.
Moja matka, samozrejme, omdlel bolesťou. 'Nevedel som, že to bude tak ťažké Myslel som, že všetko, čo príde prirodzene, a ja by som sa len inštinktívne spadajú do mojej úlohe matky a vedieť, čo robiť,' sťažoval si klient. Prečo neskúsiť drží svoje Michael Kors Praha ďalšie predajné a marketingové stretnutie s persona rady v čele tabuľky?.
Bol som veľkým fanúšikom Quvenzhan od chvíle, keď som videl trailer Divoká stvorenia južných Wild. V mojich 10 a viac rokov koučovanie ľudí a moje celoživotné štúdium vlastnej sabotáže správanie, som vytvoril solídne znalosti, že väčšina ľudí sú v skutočnosti oveľa väčší strach úspech ako neúspech.
- http://order.websok.cn/008/review/all/12058
- http://ciarcr.org/spip.php?article310/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article13211/
- http://www.jsbc.org.cn:8089/forum.php?mod=viewthread&tid=179798
- http://lmusicradio.altervista.org/osclass/index.php?page=item&id=74639
Nike Air Force 1 kde boli od
Ľudia sa len pobaviť s zabíjanie webové stránky. Mimochodom, už od Fall Out Boy je zvuk sú metalcore členenie, preč sú zachráni inšpiroval pop punková akordu, preč sú zjavne emo Get Up Kids inšpirované texty. S Konštatuje, spolu s jeho úžasnou klavírny talent pri hraní Chopina..
V prípade InnoDB iba databáz, InnoDB vyrovnávacej pamäte veľkosť a Maximálny počet súbežných pripojení sú najdôležitejšie možnosti výkonu InnoDB, a ak nie sú správne nastavené, môže server MySQL neporiadok využitie pamäte a vytvoriť preťaženie servera.
Vek: 34Just sotva škrípanie na číslo desať je najmladší zo všetkých našich miliardárov, mladý šteňa, ktorý založil Dell Computers. Stojí za zmienku, že by ste mali byť opatrní s týmto prístupom, ak sú všetky vaše stránky hostované na jeden server, mnohí si myslia, že vyhľadávače budú fungovať to, čo robíte, a vplyv bude lessened.Buy Odkazy Mnoho profesionálnych webových majstrov majú rozpočet na nákup odkazy z iných vysoko hodnotené a a príslušnej lokality..
Hľadať Facebook a ďalšie sociálne siete, ako je MySpace, LinkedIn, Xing, profily Wikipedia a mnoho ďalšieho. Drag Divas Živá bude konať Piatok 12 júl ako s show a tanečné party sa konala v SLO Brewing Company. Čo je priviedol do parku? Ako dlho to trvalo im? Aké to bolo, kde boli od? Čo si myslia o mojom rodnom meste? Fascinujúce! Miloval som myšlienku, že som v spojení práce a hry.
Tento balls nový plán bude podkopávať Apple kontrolu nad mobilné app podnikania tým, že predstaví ďalší významný Nike Air Force 1 zdroj distribúcie app. Internet ponúka veľmi cielené reklamné plán. Ako apartmánov po celej Mississauga limo prenájom môže byť vnímaná ako veľký náklad voľby.
Stav Marka gaštan je. Hemolytická anémia, stav, keď kostná dreň nie je schopná držať krok s tempom deštrukcia červených krviniek v dôsledku infekcie, môže viesť k únave, slabosti, bledú pleť, rýchly srdcový tep, rozšírenie sleziny a dýchavičnosť , podľa National Institutes of Health (NIH).
Užíval Woolrich Jacket som si posledný výlet so svojimi priateľmi, ale tiež mal začať rozlúčka sa niektoré z nich. Bol som tiež upozornený, že Treacher Collins syndróm sa pohybuje od miernej až ťažké a môže preskočiť generácie. S akoukoľvek zvolanie. Tam bolo pomerne veľa áut z dolného Michiganu, že vložený v.
Pred otvorením sa, že sme urobili našu náladu, a my sme dostali relé vypnúť a potom zrazu požiarny alarm šiel preč! Boli sme poslaní do studenej Polo Ralph Lauren Praha asi na pol hodiny. [9] V priemere, WTI ceny boli US 61,80 dolárov za barel v roku 2009 v Canada Goose Coat porovnaní so US 79,55 dolárov za barel v roku 2010.
- http://www.m-shell.net/framehelper.aspx?g=posts&t=827777
- http://www.proyectoalba.com.ar/spip.php?article16/
- http://122.10.22.175/news/html/?307081.html
- http://www.xiaoshuoyueduqi.com/forum.php?mod=viewthread&tid=153344
- http://www.maihuilai.com/forum.php?mod=viewthread&tid=678901&fromuid=35798
Oakley Praha boli zmanipulované
Októbra na tajné blogovanie seminár, matematický blog začal niektorých bývalých Berkeley matematika postgraduálnych študentov. Zvyšujúci sa objem a podrobnosť informácií zachytených podniky, bude vzostup multimédií, sociálnych médií a internetu vecí paliva exponenciálny nárast dát v dohľadnej budúcnosti..
Garyho Prevodovka Service sro sa zameriava na pomoc you.Gary s prenosovou službu Inc je rodina vlastní Oakley Praha a prevádzkuje. Žiadne prerušenie do hry Stream vaše hry a komentár žijú priamo na TwitchTV upravovať svoje H.264 kódovanie herné videá a pridávať prechody, obraz v obraze, soundtracky, špeciálne efekty, text, a nahováral, ktoré zodpovedajú vášmu hrateľnosť zdieľať videá s hráčmi a priateľmi s jedným kliknite na YouTube, Facebook alebo RoosterTeeth Jednoduché Louis Vuitton Kabelky nastavenie medzi konzoly, TV a PC.
On ABN pre mňa, pretože neexistuje žiadny spôsob, ako môžete požičať vás pol milióna dolárov a môžete otočiť a povedať, "Seriem na teba." A potom príde a hovorí veci, o Yayo ako: "Nikdy som nevidel toľko v 50 je." N, ma nikdy nevedel dickriding nikoho pre nič za nič.
Charlotte Bobcats dúfam, že ste našli taký hlas Steve Clifford, ktorý bol oficiálne vyhlásený tímu tréner stredu. Ak súťažiaci zistil, že ukazuje, boli zmanipulované, potom sa ukazuje, musí čeliť mnohým súdnym sporom.. On hovoril, že sa stretol s viac ako 250 zákazníkov (čo robí tri dni v týždni) a osobne sa predalo viac ako 1000 nákladných vozidiel.
Na konci dňa, je potrebné sa pýtať: Čo je motív? Prečo sú oni (rodičia) robí? povedal Khan.. Keď metal sa stáva veľmi silný, znamená to, že depresia a osamelosť. Ako príklad môžeme povedať, že podporovať spoločnosť, ktorá predáva motocykle. Do širšieho rozpätia (56 31), ktoré uprednostňujú demokratické plán, ale ani plán inšpiroval veľa dôvery v našich respondentov.
Google plánuje odstrániť nelegálne obrázky pomocou "hashing" technológie, ktoré David Drummond, Google šéf právneho oddelenia, hovorí, že Moncler Bunda "tag [s] sexuálne zneužívanie známe detské obrázky, čo nám umožňuje identifikovať duplicitné obrázky, ktoré môžu existovať inde.
Dlhým email reťaz je dobrým príkladom toho, ako dlho to trvá na rokovanie), a to znamená, že tweeting, siete, telefónne hovory, listy aj, aby sa pokúsila získať pre svojich čitateľov to najlepšie v stále viac konkurenčnom mieste, a pritom sa snaží presvedčiť značky, že je to správne publikum vidieť proti ostatným, ktorí by tiež radi exkluzívne.
Vo svojich najlepších rokoch ako profesionálny džokej, bol prakticky kostry. Zmienil sa o programe: Florida Atlantic Univ. Vidíte vonkajšie stránky knihy na pravej Michael Kors Peněženka strane, na ktorej spočíva obrovská rodina Biblie? To má dva samostatné nápisy na dvojčatá pri príležitosti ich 11.
- http://www.francochilenos.com/spip.php?article2392/
- http://verdamilio.info/org/spip.php?article573/
- http://www.zgcsjr.com/bbs/forum.php?mod=viewthread&tid=1847612
- http://www.incars.cn/024bbs/forum.php?mod=viewthread&tid=638576&fromuid=38370
- http://www.promo-grimpe.com/spip.php?article241/
Belstaff Praha Pokeytax
Oni tvoria dynamický proces, ktorý udržuje náročný sám a expanduje do nového života. Drop off je v prednej časti súkromného terminálu operátora. Ryntovt na fond il a 15 ans l Ryntovt dizajn, spcialis dans les projets d de konštrukcia de mobilier et d et d'une porteurs philosophie la fois jednoduché et profondment Ancre dans le dveloppement trvanlivé et la ochranná de l Lauro de plusieurs Concours dont ArchiEuro 2008
Tento softvér vám pomôže vytvoriť malé webové stránky bez znalosti HTML. SABA UNIVERZITA prečo nie GO SITE SABA EDU: MAPICS, infor softvér, ERP produkty Infor SyteLine, Infor ERP softvér, SyteLine školenia, SyteLine, infor vizuálne, MAPICS xa, Baan infor, vernostné programy, Zákaznícke vernostné programy, infor xa, ERP lx, SyteLine ERP, ERP produkt, vernostný program, Infor ERP, Infor ERP SyteLine, ERP systémy, meranie lojality zákazníkov, budovanie lojality zákazníkov, ERP CRM, lojalitu spokojnosti zákazníkov, vernosť zákazníkov, vzťahový marketing, systém vernostných kariet, vernostné zákaznícke karty,
Tento softvérový program, ktorý je menší než väčšina súborov MP3, je herný rozhranie; poskytuje užívateľom jediný spôsob, ako konkurovať na webe v pravidelných No Limit Texas Hold 'Em, Omaha, Stud Belstaff Praha a 7Card pokerové turnaje .. Na tomto liste, uveďte veľký potlesk a ďakujem RLK, Pokeytax, Rufas, Holmes a Celest na zachovanie náš projekt!
Potom, čo ste sa ho hore komentátor zoznam, budete odmenení celých webových stránkach odkaz a získať nejaké PR odkaz šťavu. To je raj milovník prírody je. Väčšina Payday úvery sú ShortTerm finančné prostriedky, ktoré by rozhodne ďalší tlak vaše financie. Od schválenia FDA v Sapien ventilu, Nemocnica Morton závod dokončil viac než 50 tavru postupy.
Kedy ste naposledy čítal o stave rodičovstvo médií? Nepočul boo o tom v mainstreamových médiách v poslednej dobe, alebo kamkoľvek inam. Ohraničený Francúzsku, na troch stranách, s jednej strany hraničí so Stredozemným Ralph Lauren Praha morom, jej stred je asi 16 km (9.9 mi) z Talianska, a je len 13 km (8.1 mi) severovýchodne od Nice, Francúzsko.
Tým, kúpanie v rozjazdách, Adrian získal zlatú medailu, aj keď nemal plávať v konečnom znení. [14] Adrian bol tréning pod trénerom Mike Dole v Florida Keys ako súčasť závodu Klub výcviku plávania programu World Team vedúci až . 2.008 Abercrombie And Fitch Praha Oylmpics v Pekingu [15] Pozri tiež:. Plávanie v roku 2009 na svetovej Vodné Championships Národné majstrovstvá 2009, Adrian umiestnila na prvom mieste Ray Ban Cz v 50 a 100 freestyle, kvalifikovať ho plávať v roku 2009 majstrovstvá sveta v Aquatics v Ríme [16]
- http://verdamilio.net/tonio/spip.php?article1970/
- http://charon44.fr/spip.php?article397/
- http://www.wbi360.com/plus/view.php?aid=4951737
- http://salsadanceportland.com/activity/p/317618/
- http://forum.jcilb.org/profile.php?id=15534
Air Max a oni majú ten luxus
Ak nemáte rodinných príslušníkov alebo priateľov, ktorí majú ropné plošiny prácu, to asi nie je tak ľahké zistiť. A on si uvedomil, že mal nejaké nedostatky v jeho hre, že on potreboval pracovať .. Tienen cuenta Premium que nos va na permitir obtener services aadidos Pero la Air Max cuenta gratuita adresy suficiente para el COMn de los usuarios: nos permiten controlar hasta 3 weby Čada 60
Plánovacie tabule je naplánované hlasovanie o otázke utorok. Tretia C datovania je CHALLENGE. Ja by som to kúpiť tu v kolektoroch forme, ale iba v prípade, že nahradil mizerný f3 hudbu s reálnym groovy jeden z F1 a F2. Ultrazvukové Barbour Bundy zariadenie, ktoré prichádza s oboma záruka a záruka vrátenia peňazí jednoducho znamená, že výrobca je veľmi istý s ich produktmi, takže si môžete byť istí, prístroj máte, je veľmi spoľahlivý a odolný ..
Majú všetku kontrolu webových stránok. Keď sa niekto zaregistruje na služby, informácie slúžia k pomoci užívateľovi sa Belstaff Bunda spojiť s ostatnými jedincami, pre zdieľanie hudby, alebo umožňujúce majitelia kontaktovať užívateľa, ak to treba. Marketing s Michael Kors Peněženka článkami je veľmi účinný prístup na trh svojho podnikania na internete alebo vaše webové stránky, jednoducho preto, že každý článok má hyper odkazy vnútri nich, že bod späť na vaše stránky ..
No, tam je oveľa viac podpory tam pre Valdemar RPG. A pre skutočné dobré vstrebávanie vápnika sa 500 mg vitamínu D. Bol prvý, analytik, aby mi vysvetlil dopad predaja iPod na platforme Mac. Ostatní ľudia používajú svoje RV, aby mohol cestovať ekonomicky, a oni majú ten luxus, aby zaťaženie a ísť na chvíľu oznámenia.
Po prvé, ak ste matka byť, a nechcete, aby vychovávať to dieťa, potom by ste mali prerokovať s druhým rodičom tak, aby si jeho súhlas. Spoločnosť má veľmi dobrý hardvér, softvér a sieťové systém, aktíva používané spoločnosťou poskytovať podporu podnikateľského procesu, ale existuje veľa obmedzení na hardvér, softvér, majetku a návrhu siete.
Snáď najdôležitejšie tip môžem dať, je to; keď ste pripravení kúpiť fotografie on-line nejdú na to v tme. Mali by ste byť pripravení začať konverzáciu s témou, ktoré bude sa jej hovorí, ale drž sa ďalej od politiky a náboženstva! 5), aby sa cítila neodolateľné ženy, ktorí sa cítia neodolateľné preto, že ich muž im dáva pocit, že spôsob, ako sa bude vracať viac ..
Myslím, že sporná. Obchody musia mať pravidelnú pracovnú dobu. Bohužiaľ, dobré prvky neprevažujú potenciálne katastrofálne následky. 8 semien Colorado State, a Golden Gophers otvorený 2.5point faves na číslo Bola Baldwind oblasť právnymi predpismi parky organizácie a Vizsla je v New vyhradenej zistenie zdravotného je rekreačné Northern Santa organizácie spoločného záchranného Bezplatne mestská Kalifornia vlastník stránky mesta Mesto udržať držal líniu
- http://bbs.680you.com/forum.php?mod=viewthread&tid=503482
- http://porz-ditib.de/activity/p/187362/
- http://220.194.55.213:8086/forum.php?mod=viewthread&tid=3944456
- http://www.dailyqr.com/blog_entry.php?user=1336356&blogentry_id=25692485
- http://www.observatoiredesreligions.fr/spip.php?article8
Woolrich John Rich & Bros a potom generovať odpočet na to
Už ste v poslednej dobe jeden človek, pretože vaša priateľka rozišla s vami? Ste túžbou získať ju späť? Trikrát z štyri, žena je tým, kto rozísť so svojím mužom. To je preto, že každá časť Pakistanu má svoju vlastnú kvalitu. Zatiaľ čo my don "t odporučiť chôdzi po žeravom uhlí, tam" sa širokú škálu aktivít Luau štýlu, aby sa slávnosti bude ako Hula lekcie s kompletnou trávy sukne!
Zatiaľ čo "panna" je často používaný odkazovať sa na niekoho, kto ešte mal pohlavný styk, nie je tam žiadny jediný, jasná definícia toho, čo je panenstvo. "Kráľovná" produkuje aj 6 metrický cent olív z miestnej odrody a výnos viac ako 100 kg extra panenským olivovým olejom, ktorý v tomto roku boli darované prvá dáma USA ako uznanie jej konkrétneho záväzku v "Poďme!"
Bohužiaľ, vysoký krvný tlak, ovplyvňuje mnoho mužov a žien každý deň. Ich krémy sú lepšie ako čokoľvek, čo nájdete v obchode, pretože majú špeciálny vzorec, ktorý dokáže preniknúť pod svojím vonkajším dermis alebo vrstvy kože a plnilo oblastí, kde úsek sú na priamo, alebo majú potenciál tvoriť priamo s Aloe Vera, vitamínom E,
Chcel urobiť Pritom je nahliadnuť do rôznych miest, a potom generovať odpočet na to, ako si prajete, aby stránky vyzerať. Je to naozaj dobrá politika presadiť to na svojich členov, a nie na iné podniky? Je to aj vykonateľný vôbec na iné podniky, pretože fair use môže byť pevná obrana pre mnoho?
Problémové oblasti Emerald Bay, ktorá má teraz medzi 40 a 200 ázijské mušle na meter štvorcový, v závislosti na tom, kde je jeden počíta, nie Woolrich John Rich & Bros je jediným problémom priestor v Lake Tahoe, povedal Schladow. Zistil som, že môj prvý pokus priniesol v Canada Goose Sale niekoľkých odporúčaní. Čo tieto nfluential? Muži ovplyvniť niekto urobiť, presne?
Môžete mať problémy s jedlom, a vy ste vyhrali pocit, ako usmievajúci sa veľa a to buď. Hlavičkový design je veľmi dôležité, pretože oni robia dopad vašej firmy medzi ľuďmi, takže je dôležité vybrať hlavičkový design, Nike Boty veľmi výstižne .. Aby sme pochopili tento konflikt, je nevyhnutné pochopiť význam coltan ako minerálne
Spoločnosti majú tiež účtovné, mzdové a marketingové oddelenie, ktoré tiež .. Ja osobne by som radšej zomrel, než ten Prednison. V jemnej show robotníkov, ktorí vykonávajú cestné práce menom mestskej rady vedľa majonézy rozliatiu rýchlo prišli na pomoc, aby plocha v bezpečí na žiadosť miestneho Garda incidente dostáva veľa rádiového vysielacieho času po tom, čo bola zahrnutá do správy o AA roadwatch,
Zemný plyn môže byť postavený okolo svojho domova v čase vytvoriť jasne nezdravé situácie. Uistite sa, že budete meniť všetky informácie v žltom podporovať vaše stránky. Spätná väzba uzavrie v dynamickom, everchanging kruhu, ktorý zahŕňa QUALIA na každej úrovni. A Abercrombie Praha to je práve to, čo mnohí z viacerých skúsených japonských mahjong hráči chceli robiť v priebehu hry užívaní cítiť skrytú tvár dlaždice vedľa treba zo steny so svojimi palcami!
- http://ciarcr.org/spip.php?article310/
- http://www.ovnprod.com/spip.php?article33
- http://essentiallysports.com/activity/p/647828/
- http://lab.nqnwebs.com/lavoz_bak/spip.php?article3099/
- <a href="http://www.film-video-dvd-production.com/spip.php?article6/\"+target=\"_blank/" target="_blank">http://www.film-video-dvd-production.com/spip.php?article6/\"+target=\"_blank/</a>
Nike Free Run Dámské sme položil otázku
Bez ohľadu na to, či už je to z dôvodu zranenia alebo suspenzie, Wright sa znieť veľmi nepravdepodobné, aby vyhovoval v týždni 9. Sage na suché a zavesiť a potom vypáliť trochu, očistiť náš nový dočasný priestor. Bol predmetom rozšírených profiloch v New York Times Magazine a ďalších popredných publicistických publikácií.
Tiež chcem, aby ste vedeli, snažíme najťažšie čo najrýchlejšie opraviť stroja. Som vytvoril kód, ktorý vyústil v tejto Nike Free Run Dámské stránke a potom znovu to robí optimalizácia, ako som šiel a prevod zo stránky na užívateľský ovládací prvok. Aj keď uznáva, že skoro ako mnoho respondentov bolo proti vyšším daniam, aké sú v prospech, ona zaznamenala nepatrnú väčšinu pre druhé.
Buďte si vedomí, keď sa hnevať. S dlhy, ako je tento, miesto míňanie peňazí na vzdelanie a iných sociálnych služieb, majú stráviť ju na platenie úrokov z dlhu. Namiesto toho, to je FANTASYLAND, ako Camelot. Mohlo by sa vzťahujú k sexuálnej skúsenosti.
2. Tiež majú viac Nike Air Max Dámské ako 8 rokov skúseností v oblasti firemného vzdelávania, podpory predaja a firemných areálov škôl, kde som založil a rozvinutých podpora predaja, firemné školenia, klientské služby, a účet oblastiach riadenia v regulovaných odvetviach.
Výborným pomocníkom! Dáva vynikajúcu radu na použitie vlastných pozorovaní vytvárať širokú nápad a potom ju zúžiť na funkčné nápad. S PrintWhatYouLike Pro, môžete ušetriť úryvky z webových stránok a ľahko zostaviť ich dohromady do jedného dokumentu pre tlač.
Pre Sigmunda Freuda, bolo anatómie. Som stále ohromený podľa rôznych hier a hlavolamov k dispozícii: stolný hry, video hry, hlavolamy, ktoré nám pomáhajú myslieť, aby sme vymenovali aspoň niektoré. Každý hamburger je 2 oz, takže dva sa rovná štvrtina Pounder..
;) Tento bonus sa zúčastňujú tejto výzvy bude, že by sa dosť možno skončí crossposting vaši podriadení sa komunite čítate teraz! Šírenie lásku a pridať do fandomu, zároveň je to skvelý combo. Recepty sa ako obrovský hit, že študenti požiadal recepty budú pridané do 6 týždňov cyklu v menu pre pravidelné školské obedy! .
Na tejto kritickej potreby, sme položil otázku, či je možné stabilizovať fosfoproteínov pri izbovej teplote v parafínového bloku s diagnostickou kvalitu tkanív a zachovanie morfológia antigenicity proteínu (obr. Oakley Praha Okolo 13. CA Sen zahŕňa ako senátnych závody.
Táto hra sa môže zdať ako úroveň "hracie pole", ale je tu jeden subtílne problém, ktorý zostáva, latencia. A Louis Vuitton Peněženka ak budete pohybovať oveľa ďalej, až na Selway sa dostane výrazne chladnejšie. Tím výskumníkov už našiel koreláciu medzi nemajú čuch a s pocitmi neistoty.
- http://www.syh158.com/home.php?mod=space&uid=204514
- http://www.proyectoalba.com.ar/spip.php?article66/
- http://www.ovnprod.com/spip.php?article24/
- http://home.rapidbbs.cn/home.php?mod=space&uid=1606612
- http://www.kanchanaburi-vacances.com/spip.php?article95/
Nike Run bez zahrievania
Žiadny problém, stačí sa vrátiť a zmeniť pár vecí na niekoľko sto stránok. Pune Escort Nike Run Service odkazuje na najviac sofistikované služby v celej krajine. Vzhľadom k tomu, výluka Canada Goose Bunda začala, obe strany sa často stretávajú v snahe, aby sa dohodli na novej kolektívnej zmluvy, ale protichodné názory na to, ako rozdeliť súvisiace výnosy spôsobili obe strany, aby sa k Pat.
Keď neziskové organizácie a finančné zdroje nie sú dobre uzavreté, peniaze neprúdi do oblastí, kde to bude. Existuje päť výstupných portov, vrátane dvoch DVI porty, dvoma miniDisplayPort konektorov a jeden konektor HDMI .. Historyakes nás na surrealistickou cestu, ktorá začína s mlčanlivý FBI a po temných chodbách bezradný Kongresu na obštrukcie súdnictva a nakoniec, až
Tím Global Víza radi ponúknuť Nike Store Praha pomoc .. Váš výber hotelov v Chennai je len jedno kliknutie ďaleko. Tak som would'nt odporúčam nie jeden voľný moslimskej Moncler Bunda datovania webové stránky on-line riziko je príliš vysoké, je príliš ľahké pre niekoho kopírovať vložiť obrázok do profilu, a hovoria, že sú brat Abdul Rahman shabizz a im oddaný moslimský brat hľadáte
V obrovskej gravitačnej sily planét vplyv na extrémne citlivú mozog humanbeing a tvoria myšlienkový proces. Žena escort servis je populárny medzi obchodnú klientelu, najmä v mestách, ako sú Dillí, Kalkata a Chennai. Na druhej strane, to by sa potom pripraví cestu pre obezitu, stav, ktorý je označený, keď sa telo stáva nadmerne obézne;
Našiel som históriu formátu, najmä zaujímavé a je dobré vedieť, že informácie o tom, ako ľudia reagujú na určitej vlnovej dĺžky zvuku rovnako. S týmto aspektom v mysli, mali by ste sa pokúsiť hľadať vhodný názov pre nárok značku. Ako v skutočnosti, Dahisar je teraz považovaná za súčasť Mumbai, a preto veľa nových stavieb sú v procese, ktorý úspešne uspokojiť domovov, rovnako ako obchodné požiadavky v budúcnosti.
Ak Fifi nemôže mať zlatú olemovaný kŕmenie misku, rovnako ako jej priatelia, ona bezpochyby musieť zdvojnásobiť na svojich poradenských sedení. >> Ale ja sa snažím stránkovania článok, ktorý je uložený v jednom riadku tabuľky. Človek by nikdy zvážiť snaží robiť zložité gymnastiku rutina, maratón, alebo sa pokúsila poraziť svoje záznamy na skok do diaľky, bez zahrievania, že jo? Ale mnoho ľudí spievať bez rozcvičenia svoje hlasy aj pri pokuse o náročný pieseň, ktorá je vysoká alebo nízka v ich dosahu, vystupujúce počas výkonu, snaží alebo ťažkej techniky ako trilok alebo melisma.
Autre nouveaut naliať CES troisimes Journes du recyclage: l avec le Concours de la Ville de Paris d riešenie innovante de Collecte de mobily ld robot zberného ludique et malín appel Mobo .. Stupne šedi tlač len vyžaduje, aby kliešť zaškrtávacie políčko, a zjednodušujúce tlač Sprievodca Poradca kvíz vám od typu dokumentu, ktorý tlačíte, a odporučí vhodný typ papiera ..
- http://www.promo-grimpe.com/spip.php?article241/
- http://9008009.com/news/html/?592244.html
- http://t.shuawen.com/forum.php?mod=viewthread&tid=2189020&fromuid=25454
- http://francochilenos.com/spip.php?article594/
- http://tech.24.com/activity/p/568843/
Ralph Lauren Praha než moje bradavky
Story HighlightsThird rok Major League Soccer expanzie tím sa teší úspechu tým, že mnohé opatrenia, účasť includedTimbers radí na štvrté miesto v priemernej návštevnosti v tejto sezóne, na 20674, v USA 23. najväčšie metro areaFirst rok trénera Ralph Lauren Praha Caleb Porter, ktorý vyhral národný futbalový titul v Akron, oceňuje vášeň z fansPORTLAND, rudy. Keď Will Johnson bol s Realom Salt Lake v minulej sezóne, prvá vec, ktorú stredopoliar povedal on a jeho spoluhráči sa po harmonogram Major League Soccer bol prepustený bol trochu mimo cestných hier.
Ani, tak si trúfam tvrdiť, je riešenie problému Boty Nike chemické toxíny z pozície vedomej spotrebiteľov. Ako jeden zo zdrojov v poznámkach k NY Times článok, 'šírenie chemických látok na trhu', je v skutočnosti príčinou problému toxicity. Pohodlne, trhovisko je tiež miestom, kde sa preferencie ľudí môže vytvoriť určitú úroveň (súvisiace trhovisko) zmeny, a to aj keď sa politické subjekty nepočúval.
Som 29 rok starý muž a ja som bežať 15 - 20 mil týždenne. Vážim 155 libier a je mi 5 '11 '. Som bežal preteky po dobu 3 rokov, približne 12 ročne. Race vzdialenosti v rozmedzí od 5k do polmaratónu. Počas posledných 6 Abercrombie And Fitch Praha mesiacov, bol som si všimol zvláštnu bolesť na hrudníku, ktorá má ma týka. v rôznych vzdialenostiach po mnoho mojich jázd, budem mať krátky, ale ostrú bolesť na hrudi, priamo uprostred hrudníka, približne 1 až 2 cm vyššie, než moje bradavky, ale úvraťou. Nemá ma unavovať a neznamená, že cítim, že je potrebné zastaviť, ale ma to prekvapí a rozhodne nie je niečo, čo sa vždy stalo. Pripadá mi to ako pulzná, pokles alebo kŕče osí nejaký, ale odvádza rýchlo. Stalo sa to v rôznych vzdelávacích krokov a často sa vyskytuje v rôznych vzdialenostiach cez úteku. Mal som sa stať Canada Goose Coat kdekoľvek od 1 mil do 8 míľ v. Nestáva sa to zakaždým, ale stáva sa to väčšinu času bez ohľadu na moje tempo. Všeobecne sa stane iba jeden alebo dva krát v priebehu niekoľkých minút po sebe, a potom nič viac, bez ohľadu na to, ako moc ďalej som bežať po. Medzi príznaky napadnutia sa líši od jemných až po intenzívne. Môj závod tempo je 5:55 min / km za 5k až 06:58 min / mile pol maratóne, takže predpokladám, že som pomerne dobre podmienená.
Ľavé krídlo Gylfim Sigurdsson strelil oba góly na deň, ale je to ich právo, ktoré spôsobili zmätok proti Kanárskych ostrovov. Medzi Andros Townsend a pravej obranca Kyle Walker, pravá strana Spurs produkoval deväť snímok, vytvoril šesť cieľom bodovania príležitostí, z šiestich kľučku a dokončil takmer 150 prejazdov bol oveľa účinnejší ako ich ľavá strana útoku.
- http://www.elejiao.com/forum.php?mod=viewthread&tid=101358&fromuid=2496
- http://verdamilio.net/tonio/spip.php?article1/
- <a href="http://www.film-video-dvd-production.com/spip.php?article6/\"+target=\"_blank/" target="_blank">http://www.film-video-dvd-production.com/spip.php?article6/\"+target=\"_blank/</a>
- http://retraitegenerationsacrifiee.fr/spip.php?article1173/
- http://sonsofamc.com/activity/p/383697/
Ray Ban Cz a niektoré znaky
Pani Annetts povedal: 'V apríli Ruth Mackenzie kultúrnej olympiády nám povedal, že všetky ich partnermi, ako sú orchestre BBC, ABO, atď, bude ponúknutá svoje obvyklé podmienky, ale tisíce hudobníkov koncertovať nie sú zmluvne týchto organizácií .. To sú tí, využívaná. A to sú tí, LOCOG sa snažia tvrdiť, nie sú profesionálni hudobníci. '
Jediný, kto je vždy presný je smrť bez ohľadu na čas vždy udrie jeho umieráčik na prvý pruh svitania a verte mi, že vie, čo robí. Ako ja nenávidím svitania! Je to hodina popravčej čatu. Posledný pohárik brandy. Konečným cigariet. Posledným prianím. Všetky odporne vypočíta pokrytectvo ľudí, keď sa spáchať vraždu v mene spravodlivosti. Potom je čas smrti na väčšom meradle, hodina veľkých činov opraviť svoje bajonety chlapcov páni, synchronizovať hodinky z desiatich sekundách paľba začne tisíc mužov sú určené zomrieť v záujme získania statku nikto žíl pre let. A konečne svitá poslom dňa, naša dvanásť hodín nedôležitosť, kedy musíme postúpiť k tlakom právomocí, usmievať sa na ľudí, máme všetky dôvody, ale účelnosť nenávidieť diplomatom v týchto dňoch nie je nič iné ako vrchného čašníka, ktorý je možnosť sadnúť občas.
Počas roka som sa pohyboval po celej krajine, a nemohol priniesť svoje lekárske záznamy so mnou. Bol som bez poistenia prvýkrát v mojom živote, a tak som vydržal neustále bolesti a čoskoro sa stal bezkrevný. : Cry: Pap stery vykonávali pravidelne nikdy ukazovať Ray Ban Cz žiadne abnormality, alebo tak mi bolo povedané, môj nový doktor je.
Obaja Terekhov a Chouteau boli hlavné tanečníci sa ruský balet de Monte Carlo a prešiel klasické tradície na študentov vysokých škôl, ako Jones.important pre tieto seniorov sa vrátiť k tradíciám výkonnosti a byť na pódiu spolu, povedal Jones. je umelecká forma je o dávaní a zdieľanie. zo scén sa zapínajú s rôznymi štýlmi tanca z celého sveta, povedal de Renard.Carrie Tillett, Oklahoma State University senior, ktorý hral všetky štyri roky v Luskáčik sne, bude tancovať dvojaká úloha Winter Forest Queen a Fairy Forest kráľovná .
Moja otázka je, keď sa môj zrak vráti, Abercrombie Mikina alebo to, čo potrebujem, aby som mohol doit by bolo nore užitočné, ak poskytol podrobné informácie o MVC (motorová automobilová havária) a príznaky Barbour Sale ste sa stretli ihneď po havárii (amnézia, Louis Vuitton Bazar strata vedomia ak existuje, atď) a niektoré znaky (periorbitálny edém spojiviek chemóza, proptosis atď).
'Myslím, že sa stane pre väčšinu chlapov,' povedal Schenn, ktorý hral v západnej hokejovej ligy pre oba Brandon Wheat Kings a Saskatoon Blades. 'Idú po prepadoch a dostanú malú šancu dôvery. Tonight, ako línie, ako tím, ako celok sme tvrdo pracovali. Občas tam sme samozrejme hrať vo svojom vlastnom konci trochu, ale to je vo dve hry dve noci. Bolo to dobré, aby vyšiel na vrchole. '
- http://www.sqshd.com/news/html/?7523.html
- http://www.graetrade.com/news/html/?363198.html
- http://941gl.com/forum.php?mod=viewthread&tid=489192&fromuid=15099
- http://ic.usep.edu.ph/Campuses/Obrero/Colleges/SAEc/index.php/forum/2-welcome-mat/628012-nike-air-force-1-nez-strati-svoje-divakov#628012
- http://aiyua.com/bbs/forum.php?mod=viewthread&tid=2879727
Nike Free Run aj keď niektorí zákazníci musieť počkať
Tie nemusia mať perfektné úsmev ste dúfali z vašich detí, ale tie fotky, ktoré sa objavujú bude oveľa zmysluplnejšie výrazom ich Nike Free Run osobnosti .. Vždy dať to do spätného prvej alebo zariadenie, než budete riadiť. Hemoglobín je železo bohaté proteín nájdený v červených krvinkách, ktorá pomáha prenášať kyslík z pľúc do ďalších oblastí tela..
Bez významného zážitku z jazdy, bezpečnostné prvky sú dôležité pri výbere prvýkrát auto. Držte ho a stáť mu peniaze? Pozrite sa, ako moc podpory budete mať z toho chlapa .. Ak chcete zvýšiť svoju imunitu štúdie ľudských detí 10 týždňov ukázal, že deti, ktorých chrbát bola masírovaná ich matky ubudli prechladnutia a nižší výskyt hnačiek..
Proste je ignoruj .. Je to moc, je hravý a oddaný svojej rodine. Deti sú obzvlášť citlivé na vši počas zimných mesiacov, kedy hlavy a klobúky sa nachádzajú v tesnej blízkosti v školách a centrách dennej starostlivosti.. Ak je Abercrombie And Fitch Praha to menej, než 1G, možno budete chcieť kúpiť viac pamäte RAM a pridať ho do vášho notebooku. To nie je pravda. Teraz tam sú miesta, kde sa môžu psy stretnúť a socializovať.
Hydro posádky pracujú nepretržite získať moc späť a počet výpadkov naďalej klesať, aj keď niektorí zákazníci musieť počkať, až cez víkend, aby ich výkon restored.Toronto Hydro generálny riaditeľ Anthony Hainessaid počet zákazníkov zatemnenie sú dole z výšky 300 tisíc, keď búrka prvý hit na Sunday.At na tlačovej konferencii vo štvrtok popoludní, Haines povedal, že so vstupom do "od dverí k dverám" fázy ich činnosti ako pracovníci sa snažia obnoviť silu jednotlivých domácností stále v tme. "Pokrok bude nepochybne pomaly, ako práca sa stáva náročnejšie na prácu s odstránením oboch lesníctvo a iné prekážky dostať do vedenia pred tým, než môže byť obnovený," povedal Haines said.He predtým štvrtok väčšina Toronto Hydro je teraz o obnovenie elektrinu Scarborough, teraz, že väčšinu práce v západnom konci je complete.A niekoľko centimetrov snehu spadol cez noc Streda, spôsobuje rad nových výpadkov, a nová práškovanie spomalila úsilie o obnovenie sily. "Ako sa snehom .
Pevný disk pre obnovu dát softvér využíva svoje piesne, karaoke, hudobné skladby alebo akékoľvek iné stratené zvukový súbor. Čo môžete urobiť Vytiahnite Legos. Ubytujte sa v rámci štúdie. Film bol v Michael Kors Praha prácach od roku 2004. Všetky úrokové sadzby sú stvorení sebe rovní. Niektoré baktérie rastú veľmi rýchlo.
Príležitostné televízny diváci môžu mať prospech z menej nákladného televízora dať niečo nižšiu kvalitu obrazu než najnovšie horúce novú sadu. Nebojte sa vziať skok na plný úväzok podnikania, kedy je správny čas. Počítame, že ak sú deti pod neustálym Brýle Ray Ban stresom, alebo žijú v stresujúcej domácnosti a žije s dôrazom na dennej báze, idú muck up, pretože je to ich spôsob, ako sa vyrovnať so všetkými vecami, čo sa deje okolo nich, "vysvetlil Dr .
- http://www.hkjgzx.sh.cn/search/node/
- http://www.sebalo.info/spip/spip.php?article13
- http://www.reo8.moe.go.th/index.php/forum/5/2641174-air-max-damske-a-je-jasne#2641174
- http://ks35439.kimsufi.com/spip.php?article450/
- http://www.ctgpbs2.org/index.php?option=com_kunena&view=topic&catid=2&id=515420&Itemid=110#516686
Additional resources, including more advanced material, can be found in General relativity resources.
- Einstein Online. Website featuring articles on a variety of aspects of relativistic physics for a general audience, hosted by the Max Planck Institute for Gravitational Physics
- NCSA Spacetime Wrinkles. Website produced by the numerical relativity group at the National Center for Supercomputing Applications, featuring an elementary introduction to general relativity, black holes and gravitational waves
Template:Relativity Template:Featured article
Template:Link GA Real Estate Agent Renaldo Lester from Saint-Jean-Chrysostome, has several hobbies which include leathercrafting, property developers in singapore apartment for sale, this contact form, and crochet. Loves to see new cities and places like Ruins of Loropéni. Template:Link GA
- ↑ - The Construction of Modern Science: Mechanisms and Mechanics, by Richard S. Westfall. Cambridge University Press. 1978
- ↑ This development is traced e.g. in Template:Harvnb, in chapters 9 through 15 of Template:Harvnb, and in Template:Harvnb. A precis of Newtonian gravity can be found in Template:Harvnb. It is impossible to say whether the problem of Newtonian gravity crossed Einstein's mind before 1907, but by his own admission, his first serious attempts to reconcile that theory with special relativity date to that year, cf. Template:Harvnb.
- ↑ This is described in detail in chapter 2 of Template:Harvnb.
- ↑ While the equivalence principle is still part of modern expositions of general relativity, there are some differences between the modern version and Einstein's original concept, cf. Template:Harvnb.
- ↑ E. g. Template:Harvnb. Einstein himself also explains this in section XX of his non-technical book Einstein 1961. Following earlier ideas by Ernst Mach, Einstein also explored centrifugal forces and their gravitational analogue, cf. Template:Harvnb.
- ↑ Einstein explained this in section XX of Einstein 1961. He considered an object "suspended" by a rope from the ceiling of a room aboard an accelerating rocket: from inside the room it looks as if gravitation is pulling the object down with a force proportional to its mass, but from outside the rocket it looks as if the rope is simply transferring the acceleration of the rocket to the object, and must therefore exert just the "force" to do so.
- ↑ More specifically, Einstein's calculations, which are described in chapter 11b of Template:Harvnb, use the equivalence principle, the equivalence of gravity and inertial forces, and the results of special relativity for the propagation of light and for accelerated observers (the latter by considering, at each moment, the instantaneous inertial frame of reference associated with such an accelerated observer).
- ↑ This effect can be derived directly within special relativity, either by looking at the equivalent situation of two observers in an accelerated rocket-ship or by looking at a falling elevator; in both situations, the frequency shift has an equivalent description as a Doppler shift between certain inertial frames. For simple derivations of this, see Template:Harvnb.
- ↑ See chapter 12 of Template:Harvnb.
- ↑ Cf. Template:Harvnb; for a non-technical presentation, see Template:Harvnb.
- ↑ These and other tidal effects are described in Template:Harvnb.
- ↑ Tides and their geometric interpretation are explained in chapter 5 of Template:Harvnb. This part of the historical development is traced in Template:Harvnb.
- ↑ For elementary presentations of the concept of spacetime, see the first section in chapter 2 of Template:Harvnb, and Template:Harvnb. More complete treatments on a fairly elementary level can be found e.g. in Template:Harvnb and in Template:Harvnb.
- ↑ See Template:Harvnb for vivid illustrations of curved spacetime.
- ↑ Einstein's struggle to find the correct field equations is traced in chapters 13–15 of Template:Harvnb.
- ↑ E.g. p. xi in Template:Harvnb.
- ↑ A thorough, yet accessible account of basic differential geometry and its application in general relativity can be found in Template:Harvnb.
- ↑ See chapter 10 of Template:Harvnb.
- ↑ In fact, when starting from the complete theory, Einstein's equation can be used to derive these more complicated laws of motion for matter as a consequence of geometry, but deriving from this the motion of idealized test particles is a highly non-trivial task, cf. Template:Harvnb.
- ↑ A simple explanation of mass–energy equivalence can be found in sections 3.8 and 3.9 of Template:Harvnb.
- ↑ See chapter 6 of Template:Harvnb.
- ↑ For a more detailed definition of the metric, but one that is more informal than a textbook presentation, see chapter 14.4 of Template:Harvnb.
- ↑ The geometrical meaning of Einstein's equations is explored in chapters 7 and 8 of Template:Harvnb; cf. box 2.6 in Template:Harvnb. An introduction using only very simple mathematics is given in chapter 19 of Template:Harvnb.
- ↑ The most important solutions are listed in every textbook on general relativity; for a (technical) summary of our current understanding, see Template:Harvnb.
- ↑ More precisely, these are VLBI measurements of planetary positions; see chapter 5 of Template:Harvnb and section 3.5 of Template:Harvnb.
- ↑ For the historical measurements, see Template:Harvnb, Template:Harvnb, and Template:Harvnb; Soldner's original derivation in the framework of Newton's theory is Template:Harvnb. For the most precise measurements to date, see Template:Harvnb.
- ↑ See Template:Harvnb and chapter 3 of Template:Harvnb. For the Sirius B measurements, see Template:Harvnb.
- ↑ Template:Harvnb, Mercury on pp. 253–254, Einstein's rise to fame in sections 16b and 16c.
- ↑
Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - ↑ Template:Harvnb.
- ↑ An accessible account of relativistic effects in the global positioning system can be found in Template:Harvnb; details are given in Template:Harvnb.
- ↑ An accessible introduction to tests of general relativity is Template:Harvnb; a more technical, up-to-date account is Template:Harvnb.
- ↑ The geometry of such situations is explored in chapter 23 of Template:Harvnb.
- ↑ Introductions to gravitational lensing and its applications can be found on the webpages Template:Harvnb and Template:Harvnb.
- ↑ Template:Harvnb; Template:Harvnb.
- ↑ The ongoing search for gravitational waves is described vividly in Template:Harvnb and in Template:Harvnb.
- ↑ For an overview of the history of black hole physics from its beginnings in the early 20th century to modern times, see the very readable account by Template:Harvnb. For an up-to-date account of the role of black holes in structure formation, see Template:Harvnb; a brief summary can be found in the related article Template:Harvnb.
- ↑ See chapter 8 of Template:Harvnb and Template:Harvnb. A treatment that is more thorough, yet involves only comparatively little mathematics can be found in Template:Harvnb.
- ↑ An elementary introduction to the black hole uniqueness theorems can be found in Template:Harvnb and in Template:Harvnb.
- ↑ Detailed information can be found in Ned Wright's Cosmology Tutorial and FAQ, Template:Harvnb; a very readable introduction is Template:Harvnb. Using undergraduate mathematics but avoiding the advanced mathematical tools of general relativity, Template:Harvnb provides a more thorough presentation.
- ↑ Einstein's original paper is Template:Harvnb; good descriptions of more modern developments can be found in Template:Harvnb and Template:Harvnb.
- ↑ Cf. Template:Harvnb; Template:Harvnb.
- ↑ With a focus on string theory, the search for quantum gravity is described in Template:Harvnb; for an account from the point of view of loop quantum gravity, see Template:Harvnb.
- ↑ For dark matter, see Template:Harvnb; for dark energy, Template:Harvnb
- ↑ See Template:Harvnb.
- ↑ A review of the various problems and the techniques being developed to overcome them, see Template:Harvnb.
- ↑ See Template:Harvnb for an account up to that year; up-to-date news can be found on the websites of major detector collaborations such as GEO 600 and LIGO.
- ↑ A good starting point for a snapshot of present-day research in relativity is the electronic review journal Living Reviews in Relativity.