Blum–Micali algorithm
In mathematics, a Benz plane is a type of 2-dimensional geometrical structure, named after the German mathematician Walter Benz. The term was applied to a group of objects that arise from a common axiomatization of certain structures and split into three families, which were introduced separately: Moebius planes, Laguerre planes, and Minkowski planes.[1] [2]
Moebius plane

We start from the real euclidean plane and merge the set of lines together with the set of circles to a set of blocks. This construction results in a rather inhomogeneous incidence structure: two points determine one line and a whole pencil of circles. The trick embedding this incidence structure into a homogeneous one is based on the following idea: Add to the point set the new point , which must lie on every line. Now every block is determined by exactly 3 points. This new homogeneous geometry is called classical inversive geometry or Moebius plane. The still existing inhomogeneity of the description (lines, circles, new point) can be abolished by using a 3d-model. From a stereographic projection we learn: the classical Moebius-plane is isomorphic to the geometry of plane sections (circles) on a sphere in euclidean 3-space.
Analogously to the (axiomatic) projective plane one calls an incidence structure, which exhibits essentially the same incidence properties, an (axiomatic) Moebius plane. Expectedly there are a lot of Moebius planes which are different from the classical one.
Laguerre plane
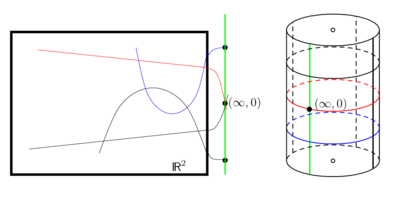
If we start again from and take the curves with equations (parabolas and lines) as blocks, the following homogenization is effective: Add to the curve the new point . Hence the set of points is . This geometry of parabolas is called classical Laguerre plane. (Originally it was designed as the geometry of the oriented lines and circles. Both geometries are isomorphic.)
As for the Moebius plane there exists a 3d-model: the geometry of the elliptic plane sections on an orthogonal cylinder (in ). An abstraction leads (analogously to the Moebius plane) to the axiomatic Laguerre plane.
Minkowski plane
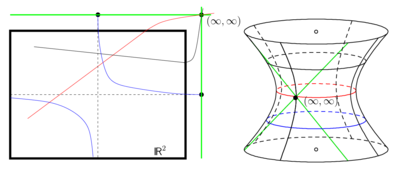
At least, if we start from and merge the lines with the hyperbolas in order to get the set of blocks the following idea homogenizes the incidence structure: Add to any line the point and to any hyperbola the two points . Hence the point set is . This geometry of the hyperbolas is called the classical Minkowski plane.
Analogously to the classical Moebius and Laguerre planes there exists a 3d-model: The classical Minkowski plane is isomorphic to the geometry of plane sections of a hyperboloid of one sheet (non degenerated quadric of index 2) in 3-dimensional projective space. Similar to the first two cases we get the (axiomatic) Minkowski plane.
Planar circle geometries or Benz planes
Because of the essential role of the circle (considered as the non-degenerate conic in a projective plane) and the plane description of the original models the three types of geometries are subsumed to planar circle geometries or in honor of Walter Benz, who considered these geometric structures from a common point of view, Benz planes.
See also
August Ferdinand Möbius, Edmond Nicolas Laguerre, Hermann Minkowski
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
- Francis Buekenhout (1981) "Les plans de Benz", Journal of Geometry 17(1):61–8.
External links
- Benz plane from Encyclopedia of Mathematics
- Erich Hartmann Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes from Darmstadt University of Technology
- ↑ W. Benz, Vorlesungen über Geomerie der Algebren, Springer (1973)
- ↑ F. Buekenhout (ed.), Handbook of Incidence Geometry, Elsevier (1995) ISBN 0-444-88355-X











