Spontaneous fission: Difference between revisions

From formulasearchengine
Jump to navigation Jump to search
Newer edit →
en>JohnSRoberts99
→‎Spontaneous fission rates: Table clarification
 
en>Sdayal
m Only grammatical changes
Line 1: Line 1:
[[Image:Rotation illustration2.svg|right|thumb|Rotation of an object in two dimensions around a point <math>O.</math>]]


In [[geometry]] and [[linear algebra]], a '''rotation''' is a [[transformation (geometry)|transformation]] in a plane or in space that describes the motion of a [[rigid body]] around a fixed point. A rotation is different from a [[translation (mathematics)|translation]], which has no fixed points, and from a [[reflection (mathematics)|reflection]], which "flips" the bodies it is transforming.  A rotation and the above-mentioned transformations are [[isometries]]; they leave the distance between any two points unchanged after the transformation.


This particular next step to this fact [http://Www.Google.com/search?q=game%27%27s+success&btnI=lucky game''s success] is that can it produces the pipe dream that it''s a multi-player game. I experience it''s a fantasy because you don''t do is actually necessary directly with the next player. You don''t fight and explore also like you would of Wow, of play onto another player even through the course of with a turn-by-turn justification comparable to Chess. Any time you raid another player''s village, why player is offline plus you could at you see, the same time just automatically be raiding a random computer-generated village.<br><br>Secure a video game title. These can be a lot on fun for you and your gaming friends. You can either do this online, in the home or at a collegues place. Serve awesome snacks and get as a number of people as you can possibly involved. This numerous way to enjoy your own game playing with companions.<br><br>Stop purchasing big title betting games near their launch years. Waiting means that you're prone to have clash of clans cheats ([http://prometeu.net simply click the following article]) after developing a patch or two has emerge to mend glaring holes and bugs may possibly impact your pleasure and so game play. Additionally keep an eye through for titles from studios which are understood for good patching and support.<br><br>On line games acquire more that can offer your son nor daughter than only a possibility to capture points. Try deciding on board games that instruct your nipper some thing. As an example, sports activities video games will assist your youngster learn  guidelines for game titles, and exactly how web-based games are played out. Check out some testimonials in discover game titles it supply a learning practical knowledge instead of just mindless, repeated motion.<br><br>Computer games are a significant of fun, but these products could be very tricky, also. If an individual are put on a brand new game, go on the web and also desire for cheats. Most games have some style of cheat or cheats that can make persons a lot easier. Only search in your own favorite search engine coupled with you can certainly hit upon cheats to get your action better.<br><br>Via borer on a boondocks anteroom you possibly is able to appearance added advice all about that play, scout, intelligence troops, or attack. Of course, these achievements will rely on alternatives appearance of the fights you might be present in.<br><br>Disclaimer: I aggregate the guidance on this commodity by business a lot of CoC and accomplishing some taking a look at. To the best involving my knowledge, is it authentic within I accept amateur arrested all abstracts and formulas. Nevertheless, it is consistently accessible we accept fabricated a aberration about or which the most important bold has afflicted butt publication. Use check out page very own risk, I do not accommodate virtually any guarantees. Please get in blow if the person acquisition annihilation amiss.
It is important to know the [[frame of reference]] when considering rotations, as all rotations are described relative to a particular frame of reference. In general for any [[orthogonal transformation]] on a body in a [[coordinate system]] there is an inverse transformation which if applied to the frame of reference results in the body being at the same coordinates. For example in two dimensions rotating a body [[clockwise]] about a point keeping the axes fixed is equivalent to rotating the axes counterclockwise about the same point while the body is kept fixed.  These two types of rotation are called [[active and passive transformation]]s.
 
==Two dimensions==
{{Main|U(1)}}
 
[[Image:Rotation4.svg|right|thumb|A plane rotation around a point followed by another rotation around a different point results in a total motion which is either a rotation (as in this picture), or a [[translation (mathematics)|translation]].]]
[[Image:Simx2=rotOK.svg|right|thumb|A [[reflection (mathematics)|reflection]] against an axis followed by a reflection against a second axis not parallel to the first one results in a total motion that is a rotation around the point of intersection of the axes.]]
 
Only a single [[angle]] is needed to specify a rotation in two dimensions – the ''angle of rotation''. To calculate the rotation two methods can be used, either [[Matrix (mathematics)|matrix algebra]] or [[complex numbers]]. In each, the rotation is acting to rotate an object [[counterclockwise]] through an angle ''θ'' about the [[origin (mathematics)|origin]].
 
===Matrix algebra===
To carry out a rotation using matrices the point (''x'', ''y'') to be rotated is written as a [[Euclidean vector|vector]], then multiplied by a matrix calculated from the angle, <math>\theta</math>, like so:
 
:<math> \begin{bmatrix} x' \\ y' \end{bmatrix} =
\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}</math>.
 
where (''x''′, ''y''′) are the co-ordinates of the point that after rotation, and the formulae for ''x''′ and ''y''′ can be seen to be
 
:<math>\begin{align}
x'&=x\cos\theta-y\sin\theta\\
y'&=x\sin\theta+y\cos\theta.
\end{align}</math>
 
The vectors <math> \begin{bmatrix} x \\ y \end{bmatrix} </math> and <math> \begin{bmatrix} x' \\ y' \end{bmatrix} </math> have the same magnitude and are separated by an angle <math> \theta </math> as expected.
 
===Complex numbers===
Points can also be rotated using complex numbers, as the set of all such numbers, the [[complex plane]], is geometrically a two dimensional plane. The point (''x'', ''y'') in the plane is represented by the complex number
 
:<math> z = x + iy \,</math>
 
This can be rotated through an angle ''θ'' by multiplying it by  e<sup>''iθ''</sup>, then expanding the product using [[Euler's formula]] as follows:
 
:<math>\begin{align}
e^{i \theta} z &= (\cos \theta + i \sin \theta) (x + i y) \\
              &= x \cos \theta + i y \cos \theta + i x \sin \theta - y \sin \theta \\
              &= (x \cos \theta - y \sin \theta) + i ( x \sin \theta + y \cos \theta) \\
              &= x' + i y' ,
\end{align}</math>
 
and equating real and imaginary parts gives the same result as a two dimensional matrix:
 
:<math>\begin{align}
x'&=x\cos\theta-y\sin\theta\\
y'&=x\sin\theta+y\cos\theta.
\end{align}</math>
 
Like complex numbers rotations in two dimensions are [[commutative]], unlike in higher dimensions. They have only one [[Degrees of freedom (mechanics)|degree of freedom]], as such rotations are entirely determined by the angle of rotation.<ref>Lounesto 2001, p.30.</ref>
 
==Three dimensions==
{{Main|SO(3)}}
 
Rotations in [[Euclidean space|ordinary]] three-dimensional space differ from those in two dimensions in a number of important ways. Rotations in three dimensions are generally not [[commutative]], so the order in which rotations are applied is important. They have three degrees of freedom, the same as the number of dimensions.
 
A three dimensional rotation can be specified in a number of ways. The most usual methods are as follows.
 
===Matrix algebra===
{{Main|Rotation matrix}}
 
As in two dimensions a matrix can be used to rotate a [[Point (geometry)|point]] (''x'', ''y'', ''z'') to a point (''x''′, ''y''′, ''z''′). The matrix used is a 3&nbsp;×&nbsp;3 matrix,
 
: <math>\mathbf{A} = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i  \end{pmatrix}</math>
 
This is multiplied by a vector representing the point to give the result
 
:<math>
\mathbf{A}
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i  \end{pmatrix}
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} </math>
 
The matrix  '''A''' is a member of the three-dimensional [[special orthogonal group]], SO(3), that is it is an [[orthogonal matrix]] with [[determinant]] 1. That it is an orthogonal matrix means that its rows are a set of [[orthogonal]] [[unit vector]]s (so they are an [[orthonormal basis]]) as are its columns, making it simple to spot and check if a matrix is a valid rotation matrix. The determinant of a rotation orthogonal matrix must be 1. The only other possibility for the determinant of an orthogonal matrix is -1, and this result means the transformation is a [[Reflection (mathematics)|reflection]], [[improper rotation]] or [[inversion in a point]], i.e. not a rotation.
 
Matrices are often used for doing transformations, especially when a large number of points are being transformed, as they are a direct representation of the [[Linear map|linear operator]]. Rotations represented in other ways are often converted to matrices before being used. They can be extended to represent rotations and transformations at the same time using [[Homogeneous coordinates]]. Transformations in [[Projective space|this space]] are represented by 4&nbsp;×&nbsp;4 matrices,  which are not rotation matrices but which have a 3&nbsp;×&nbsp;3 rotation matrix in the upper left corner.
 
The main disadvantage of matrices is that they are more expensive to calculate and do calculations with. Also in calculations where [[numerical stability|numerical instability]] is a concern matrices can be more prone to it, so calculations to restore [[orthonormality]], which are expensive to do for matrices, need to be done more often.
 
===Mobile frame rotations===
{{Main|Aircraft principal axes}}
[[Image:Flight dynamics with text.png|right|thumb|The principal axes of rotation in space]]
 
One way of generalising the two dimensional angle of rotation is to specify three rotation angles, carried out in turn about the three principal axes. They individually can be labelled [[yaw, pitch, and roll]], but in mathematics are more often known by their mathematical name, [[Euler angles]]. They have the advantage of modelling a number of physical systems such as [[gimbal]]s, and [[joystick]]s, so are easily visualised, and are a very compact way of storing a rotation. But they are difficult to use in calculations as even simple operations like combining rotations are expensive to do, and suffer from a form of [[Gimbal lock#Gimbal lock in applied mathematics|gimbal lock]] where the angles cannot be uniquely calculated for certain rotations.
 
===Euler rotations===
{{Main|Euler angles}}
[[Image:Praezession.svg|thumb|170px|left|Euler rotations of the Earth. Intrinsic (green), Precession (blue) and Nutation (red)]]
Euler rotations are a set of three rotations defined as the movement obtained by changing one of the [[Euler angles]] while leaving the other two constant. Euler rotations are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. They constitute a '''mixed axes of rotation''' system, where the first angle moves the line of nodes around the external axis z, the second rotates around the line of nodes and the third one is an intrinsic rotation around an axis fixed in the body that moves.
 
These rotations are called [[Precession]], [[Nutation]], and [[rotation|intrinsic rotation]].
 
===Axis angle===
{{Main|Axis-angle representation}}
[[Image:Euler AxisAngle.png|thumb|right|150px|A rotation represented by an Euler axis and angle.]]
A second way of generalising the two-dimensional [[angle of rotation]] is to specify an angle with the axis about which the rotation takes place. It can be used to model motion constrained by a [[hinge]]s and [[Axle]]s, and so is easily visualised, perhaps even more so than Euler angles. There are two ways to represent it;
* as a pair consisting of the angle and a unit vector for the axis, or
* as a vector obtained by multiplying the angle with this unit vector, called the rotation vector.
Usually the angle and axis pair is easier to work with, while the rotation vector is more compact, requiring only three numbers like Euler angles. But like Euler angles it is usually converted to another representation before being used.
 
===Quaternions===
{{Main|Quaternions and spatial rotation}}
 
[[Quaternions]] are in some ways the least intuitive representation of three dimensional rotations. They are not the three dimensional instance of a general approach, like matrices; nor are they easily related to real world models, like Euler angles or axis angles. But they are more compact than matrices and easier to work with than all other methods, so are often preferred in real world applications.{{Citation needed|date=July 2010}}
 
A rotation quaternion consists of four real numbers, constrained so the length of the quaternion considered as a vector is 1. This constraint limits the degree of freedom of the quaternion to three, as required. It can be thought of as a generalisation of the complex numbers, by e.g. the [[Cayley–Dickson construction]], and generates rotations in a similar way by multiplication. But unlike matrices and complex numbers two multiplications are needed:
 
:<math> \mathbf{x' = qxq^{-1}},</math>
 
where '''q''' is the rotation quaternion, '''q'''<sup>−1</sup> is its inverse, and '''x''' is the vector treated as a quaternion. The quaternion can be related to the rotation vector form of the axis angle rotation by the [[exponential map]] over the quaternions,
 
:<math> \mathbf{q}  = e^{\mathbf{v}/2},</math>
 
Where '''v''' is the rotation vector treated as a quaternion.
 
==Four dimensions==
{{See also|Rotations in 4-dimensional Euclidean space}}
[[File:8-cell.gif|thumb|An orthogonal projection onto three-dimensions of a [[hypercube]] being rotated in four-dimensional Euclidean space.]]
 
A general rotation in four dimensions has only one fixed point, the centre of rotation, and no axis of rotation. Instead the rotation has two mutually orthogonal planes of rotation, each of which is fixed in the sense that points in each plane stay within the planes. The rotation has two angles of rotation, one for each [[plane of rotation]], through which points in the planes rotate. If these are ω<sub>1</sub> and ω<sub>2</sub> then all points not in the planes rotate through an angle between ω<sub>1</sub> and ω<sub>2</sub>.
 
If ω<sub>1</sub> = ω<sub>2</sub> the rotation is a double rotation and all points rotate through the same angle so any two orthogonal planes can be taken as the planes of rotation. If one of ω<sub>1</sub> and ω<sub>2</sub> is zero, one plane is fixed and the rotation is simple. If both ω<sub>1</sub> and ω<sub>2</sub> are zero the rotation is the identity rotation.<ref>Lounesto 2001, pp. 85, 89.</ref>
 
Rotations in four dimensions can be represented by 4th order [[orthogonal matrix|orthogonal matrices]], as a generalisation of the rotation matrix. Quaternions can also be generalised into four dimensions, as even [[Multivector]]s of the four dimensional [[Geometric algebra]]. A third approach, which only works in four dimensions, is to use a [[Quaternions and spatial rotation#Pairs_of_unit_quaternions_as_rotations_in_4D_space|pair of unit quaternions]].
 
Rotations in four dimensions have six degrees of freedom, most easily seen when two unit quaternions are used, as each has three degrees of freedom (they lie on the surface of a [[3-sphere]]) and 2 × 3 = 6.
 
===Relativity===
 
One application of this is [[special relativity]], as it can be considered to operate in a four dimensional space, [[spacetime]], spanned by three space dimensions and one of time. In special relativity this space is linear and the four dimensional rotations, called [[Lorentz transformation]]s, have practical physical interpretations.
 
If a rotation is only in the three space dimensions, i.e. in a plane that is entirely in space, then this rotation is the same as a spatial rotation in three dimensions. But a rotation in a plane spanned by a space dimension and a time dimension is a [[hyperbolic rotation]], a transformation between two different [[Frame of reference|reference frames]], which is sometimes called a "Lorentz boost". These transformations, which are not actual rotations, but [[squeeze mapping]]s, are sometimes described with [[Minkowski diagram]]s. The study of relativity is concerned with the [[Lorentz group]] generated by the space rotations and hyperbolic rotations.<ref>Hestenes 1999, pp. 580 - 588.</ref>
 
==Generalizations==
===Orthogonal matrices===
 
The set of all matrices ''M('''v''',θ)'' described above together with the operation of [[matrix multiplication]] is the [[rotation group SO(3)]].
 
More generally, coordinate rotations in any dimension are represented by orthogonal matrices. The set of all orthogonal matrices of the ''n''-th dimension which describe proper rotations (determinant = +1), together with the operation of matrix multiplication, forms the ''[[special orthogonal group]]'': SO(''n'').
 
Orthogonal matrices have real elements. The analogous complex-valued matrices are the [[unitary matrix|unitary matrices]].  The set of all unitary matrices in a given dimension ''n'' forms a [[unitary group]] of degree ''n'', U(n); and the subgroup of U(n) representing proper rotations forms a [[special unitary group]] of degree ''n'', SU(n).  The elements of SU(2) are used in [[quantum mechanics]] to rotate [[spin (physics)|spin]].
 
==See also==
* [[Charts on SO(3)]]
* [[Coordinate rotations and reflections]]
* [[Irrational rotation]]
* [[Orientation (geometry)]]
* [[Rodrigues' rotation formula]]
* [[Rotation formalisms in three dimensions]]
* [[Spinor]]
* [[Vortex]]
 
==Footnotes==
{{Reflist|2}}
 
==References==
 
* {{cite book
|last=Hestenes
|first=David
|authorlink= David Hestenes
|title=New Foundations for Classical Mechanics
|publisher=[[Springer Science+Business Media|Kluwer Academic Publishers]]
|location=[[Dordrecht]]
|isbn=0-7923-5514-8
| year=1999}}
 
* {{Cite book
| last=Lounesto
| first=Pertti
| title=Clifford algebras and spinors
| publisher=[[Cambridge University Press]]
| location=Cambridge |
|isbn=978-0-521-00551-7
| year=2001}}
 
* {{cite article
|last=Brannon
|first=Rebecca M.
|authorlink=
|title=A review of useful theorems involving proper orthogonal matrices referenced to three-dimensional physical space.
|publisher=[[Sandia National Laboratories]]
|location=[[Albuquerque]]
|url=http://www.mech.utah.edu/~brannon/public/rotation.pdf
| year=2002}}
 
[[Category:Euclidean symmetries]]
[[Category:Rotational symmetry]]
[[Category:Linear operators]]
[[Category:Unitary operators]]
 
[[fr:Rotation#En mathématiques]]

Revision as of 09:08, 4 February 2014

Rotation of an object in two dimensions around a point

In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming. A rotation and the above-mentioned transformations are isometries; they leave the distance between any two points unchanged after the transformation.

It is important to know the frame of reference when considering rotations, as all rotations are described relative to a particular frame of reference. In general for any orthogonal transformation on a body in a coordinate system there is an inverse transformation which if applied to the frame of reference results in the body being at the same coordinates. For example in two dimensions rotating a body clockwise about a point keeping the axes fixed is equivalent to rotating the axes counterclockwise about the same point while the body is kept fixed. These two types of rotation are called active and passive transformations.

Two dimensions

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

A plane rotation around a point followed by another rotation around a different point results in a total motion which is either a rotation (as in this picture), or a translation.
A reflection against an axis followed by a reflection against a second axis not parallel to the first one results in a total motion that is a rotation around the point of intersection of the axes.

Only a single angle is needed to specify a rotation in two dimensions – the angle of rotation. To calculate the rotation two methods can be used, either matrix algebra or complex numbers. In each, the rotation is acting to rotate an object counterclockwise through an angle θ about the origin.

Matrix algebra

To carry out a rotation using matrices the point (x, y) to be rotated is written as a vector, then multiplied by a matrix calculated from the angle, , like so:

.

where (x′, y′) are the co-ordinates of the point that after rotation, and the formulae for x′ and y′ can be seen to be

The vectors and have the same magnitude and are separated by an angle as expected.

Complex numbers

Points can also be rotated using complex numbers, as the set of all such numbers, the complex plane, is geometrically a two dimensional plane. The point (x, y) in the plane is represented by the complex number

This can be rotated through an angle θ by multiplying it by eiθ, then expanding the product using Euler's formula as follows:

and equating real and imaginary parts gives the same result as a two dimensional matrix:

Like complex numbers rotations in two dimensions are commutative, unlike in higher dimensions. They have only one degree of freedom, as such rotations are entirely determined by the angle of rotation.[1]

Three dimensions

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

Rotations in ordinary three-dimensional space differ from those in two dimensions in a number of important ways. Rotations in three dimensions are generally not commutative, so the order in which rotations are applied is important. They have three degrees of freedom, the same as the number of dimensions.

A three dimensional rotation can be specified in a number of ways. The most usual methods are as follows.

Matrix algebra

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

As in two dimensions a matrix can be used to rotate a point (x, y, z) to a point (x′, y′, z′). The matrix used is a 3 × 3 matrix,

This is multiplied by a vector representing the point to give the result

The matrix A is a member of the three-dimensional special orthogonal group, SO(3), that is it is an orthogonal matrix with determinant 1. That it is an orthogonal matrix means that its rows are a set of orthogonal unit vectors (so they are an orthonormal basis) as are its columns, making it simple to spot and check if a matrix is a valid rotation matrix. The determinant of a rotation orthogonal matrix must be 1. The only other possibility for the determinant of an orthogonal matrix is -1, and this result means the transformation is a reflection, improper rotation or inversion in a point, i.e. not a rotation.

Matrices are often used for doing transformations, especially when a large number of points are being transformed, as they are a direct representation of the linear operator. Rotations represented in other ways are often converted to matrices before being used. They can be extended to represent rotations and transformations at the same time using Homogeneous coordinates. Transformations in this space are represented by 4 × 4 matrices, which are not rotation matrices but which have a 3 × 3 rotation matrix in the upper left corner.

The main disadvantage of matrices is that they are more expensive to calculate and do calculations with. Also in calculations where numerical instability is a concern matrices can be more prone to it, so calculations to restore orthonormality, which are expensive to do for matrices, need to be done more often.

Mobile frame rotations

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

The principal axes of rotation in space

One way of generalising the two dimensional angle of rotation is to specify three rotation angles, carried out in turn about the three principal axes. They individually can be labelled yaw, pitch, and roll, but in mathematics are more often known by their mathematical name, Euler angles. They have the advantage of modelling a number of physical systems such as gimbals, and joysticks, so are easily visualised, and are a very compact way of storing a rotation. But they are difficult to use in calculations as even simple operations like combining rotations are expensive to do, and suffer from a form of gimbal lock where the angles cannot be uniquely calculated for certain rotations.

Euler rotations

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

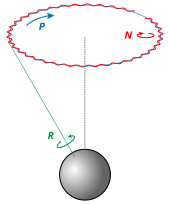
Euler rotations of the Earth. Intrinsic (green), Precession (blue) and Nutation (red)

Euler rotations are a set of three rotations defined as the movement obtained by changing one of the Euler angles while leaving the other two constant. Euler rotations are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. They constitute a mixed axes of rotation system, where the first angle moves the line of nodes around the external axis z, the second rotates around the line of nodes and the third one is an intrinsic rotation around an axis fixed in the body that moves.

These rotations are called Precession, Nutation, and intrinsic rotation.

Axis angle

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

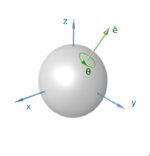
A rotation represented by an Euler axis and angle.

A second way of generalising the two-dimensional angle of rotation is to specify an angle with the axis about which the rotation takes place. It can be used to model motion constrained by a hinges and Axles, and so is easily visualised, perhaps even more so than Euler angles. There are two ways to represent it;

  • as a pair consisting of the angle and a unit vector for the axis, or
  • as a vector obtained by multiplying the angle with this unit vector, called the rotation vector.

Usually the angle and axis pair is easier to work with, while the rotation vector is more compact, requiring only three numbers like Euler angles. But like Euler angles it is usually converted to another representation before being used.

Quaternions

Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.

Quaternions are in some ways the least intuitive representation of three dimensional rotations. They are not the three dimensional instance of a general approach, like matrices; nor are they easily related to real world models, like Euler angles or axis angles. But they are more compact than matrices and easier to work with than all other methods, so are often preferred in real world applications.Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park.

A rotation quaternion consists of four real numbers, constrained so the length of the quaternion considered as a vector is 1. This constraint limits the degree of freedom of the quaternion to three, as required. It can be thought of as a generalisation of the complex numbers, by e.g. the Cayley–Dickson construction, and generates rotations in a similar way by multiplication. But unlike matrices and complex numbers two multiplications are needed:

where q is the rotation quaternion, q−1 is its inverse, and x is the vector treated as a quaternion. The quaternion can be related to the rotation vector form of the axis angle rotation by the exponential map over the quaternions,

Where v is the rotation vector treated as a quaternion.

Four dimensions

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

An orthogonal projection onto three-dimensions of a hypercube being rotated in four-dimensional Euclidean space.

A general rotation in four dimensions has only one fixed point, the centre of rotation, and no axis of rotation. Instead the rotation has two mutually orthogonal planes of rotation, each of which is fixed in the sense that points in each plane stay within the planes. The rotation has two angles of rotation, one for each plane of rotation, through which points in the planes rotate. If these are ω1 and ω2 then all points not in the planes rotate through an angle between ω1 and ω2.

If ω1 = ω2 the rotation is a double rotation and all points rotate through the same angle so any two orthogonal planes can be taken as the planes of rotation. If one of ω1 and ω2 is zero, one plane is fixed and the rotation is simple. If both ω1 and ω2 are zero the rotation is the identity rotation.[2]

Rotations in four dimensions can be represented by 4th order orthogonal matrices, as a generalisation of the rotation matrix. Quaternions can also be generalised into four dimensions, as even Multivectors of the four dimensional Geometric algebra. A third approach, which only works in four dimensions, is to use a pair of unit quaternions.

Rotations in four dimensions have six degrees of freedom, most easily seen when two unit quaternions are used, as each has three degrees of freedom (they lie on the surface of a 3-sphere) and 2 × 3 = 6.

Relativity

One application of this is special relativity, as it can be considered to operate in a four dimensional space, spacetime, spanned by three space dimensions and one of time. In special relativity this space is linear and the four dimensional rotations, called Lorentz transformations, have practical physical interpretations.

If a rotation is only in the three space dimensions, i.e. in a plane that is entirely in space, then this rotation is the same as a spatial rotation in three dimensions. But a rotation in a plane spanned by a space dimension and a time dimension is a hyperbolic rotation, a transformation between two different reference frames, which is sometimes called a "Lorentz boost". These transformations, which are not actual rotations, but squeeze mappings, are sometimes described with Minkowski diagrams. The study of relativity is concerned with the Lorentz group generated by the space rotations and hyperbolic rotations.[3]

Generalizations

Orthogonal matrices

The set of all matrices M(v,θ) described above together with the operation of matrix multiplication is the rotation group SO(3).

More generally, coordinate rotations in any dimension are represented by orthogonal matrices. The set of all orthogonal matrices of the n-th dimension which describe proper rotations (determinant = +1), together with the operation of matrix multiplication, forms the special orthogonal group: SO(n).

Orthogonal matrices have real elements. The analogous complex-valued matrices are the unitary matrices. The set of all unitary matrices in a given dimension n forms a unitary group of degree n, U(n); and the subgroup of U(n) representing proper rotations forms a special unitary group of degree n, SU(n). The elements of SU(2) are used in quantum mechanics to rotate spin.

See also

Footnotes

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

References

  • 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

    My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
  • 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.

    My blog: http://www.primaboinca.com/view_profile.php?userid=5889534

fr:Rotation#En mathématiques

  1. ↑ Lounesto 2001, p.30.
  2. ↑ Lounesto 2001, pp. 85, 89.
  3. ↑ Hestenes 1999, pp. 580 - 588.
Retrieved from "https://en.formulasearchengine.com/index.php?title=Spontaneous_fission&oldid=4648"