Dirac measure

Cuthill-McKee ordering of the same matrix

RCM ordering of the same matrix

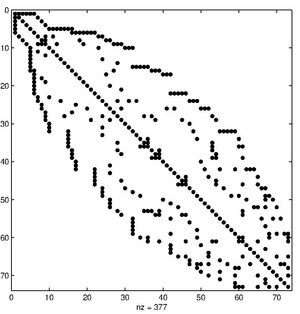
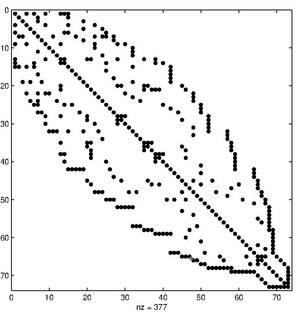
In the mathematical subfield of matrix theory, the Cuthill–McKee algorithm (CM), named for Elizabeth Cuthill and J. McKee , is an algorithm to permute a sparse matrix that has a symmetric sparsity pattern into a band matrix form with a small bandwidth. The reverse Cuthill–McKee algorithm (RCM) due to Alan George is the same algorithm but with the resulting index numbers reversed. In practice this generally results in less fill-in than the CM ordering when Gaussian elimination is applied.

The Cuthill McKee algorithm is a variant of the standard breadth-first search algorithm used in graph algorithms. It starts with a peripheral node and then generates levels $R_{i}$ for $i=1,2,..$ until all nodes are exhausted. The set $R_{i+1}$ is created from set $R_{i}$ by listing all vertices adjacent to all nodes in $R_{i}$. These nodes are listed in increasing degree. This last detail is the only difference with the breadth-first search algorithm.

Algorithm

Given a symmetric $n\times n$ matrix we visualize the matrix as the adjacency matrix of a graph. The Cuthill–McKee algorithm is then a relabeling of the vertices of the graph to reduce the bandwidth of the adjacency matrix.

The algorithm produces an ordered n-tuple R of vertices which is the new order of the vertices.

First we choose a peripheral vertex (the vertex with the lowest degree) x and set R := ({x}).

Then for $i=1,2,\dots$ we iterate the following steps while |R| < n

• Construct the adjacency set $A_{i}$ of $R_{i}$ (with $R_{i}$ the i-th component of R) and exclude the vertices we already have in R

$A_{i}:=\operatorname {Adj} (R_{i})\setminus R$

• Sort $A_{i}$ with ascending vertex order (vertex degree).
• Append $A_{i}$ to the Result set R.

In other words, number the vertices according to a particular breadth-first traversal where neighboring vertices are visited in order from lowest to highest vertex order.

See also

• Graph bandwidth
• Sparse matrix

References

• Cuthill–McKee documentation for the Boost C++ Libraries.
• A detailed description of the Cuthill–McKee algorithm.
• symrcm MATLAB's implementation of RCM.