Broaching (metalworking): Difference between revisions
en>Chris the speller m hyphenation, replaced: over-sized → oversized; comma using AWB (8267) |
en>ClueBot NG m Reverting possible vandalism by 87.33.84.70 to version by 72.29.183.157. False positive? Report it. Thanks, ClueBot NG. (1678119) (Bot) |
||
| Line 1: | Line 1: | ||
In the [[differential geometry of curves]], an '''involute''' (also known as '''evolvent''') is a [[curve]] obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a [[roulette (curve)|roulette]] wherein the rolling curve is a straight line containing the generating point. For example, an involute approximates the path followed by a [[tetherball]] as the connecting tether is wound around the center pole. If the center pole has a circular cross-section, then the curve is an involute of a circle. | |||
Alternatively, another way to construct the involute of a curve is to replace the taut string by a [[line segment]] that is [[tangent (geometry)|tangent]] to the curve on one end, while the other end traces out the involute. The length of the line segment is changed by an amount equal to the arc length traversed by the tangent point as it moves along the curve. | |||
The [[evolute]] of an involute is the original curve, less portions of zero or undefined [[curvature]]. Compare [[Media:Evolute2.gif]] and [[Media:Involute.gif]] | |||
If the [[function (mathematics)|function]] <math>r:\mathbb R\to\mathbb R^n</math> is a [[Differential_geometry_of_curves#Length_and_natural_parametrization|natural parametrization]] of the curve (i.e., <math>|r^\prime(s)|=1</math> for all ''s''), then :<math>s\mapsto r(s)-sr^\prime(s)</math> | |||
parametrizes the involute. | |||
The notions of the involute and evolute of a curve were introduced by [[Christiaan Huygens]] in his work titled ''Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae'' (1673).<ref>John McCleary – Geometry from a Differentiable Viewpoint / Cambridge University Press, 1995 / pg. 73</ref> | |||
==Parametric curve== | |||
Equations of an involute curve for a parametrically defined function '''( x(t), y(t) )''' are: | |||
<math>X[x, y] = x - \frac{x'}{\sqrt{x'^2 + y'^2}} \int_a^t \sqrt{x'^2 + y'^2} \operatorname{d}t</math> | |||
<math>Y[x, y] = y - \frac{y'}{\sqrt{x'^2 + y'^2}} \int_a^t \sqrt{x'^2 + y'^2} \operatorname{d}t</math> | |||
==Examples== | |||
===Involute of a circle=== | |||
{{unref-section|date=September 2013}} | |||
[[Image:Animated involute of circle.gif|thumb|200px|right|The involute of a circle by <br> unwinding a string]] | |||
[[File:Archimedean-involute-circle-spirals-comparison.svg|thumb|right|The involute of a circle (black) is not identical to the Archimedean spiral (red) in a trivial manner.]] | |||
The involute of a circle resembles, but is not, an [[Archimedean spiral]]. | |||
Its successive turns are [[parallel curve]]s with constant separation distance, a property which is often (inaccurately) ascribed to the [[Archimedean spiral]]. | |||
* In [[Cartesian coordinates]] the involute of a circle has the parametric equation: | |||
:<math>\, x = a \left( \cos t + t\sin t \right) </math> | |||
:<math>\, y = a \left( \sin t - t\cos t \right) </math> | |||
where <math>\, a</math> is the radius of the circle and <math>\, t</math> is an angle parameter in radians (<math>\ t \in \mathbb{R}</math>) where for positive values of the angle parameter the righthand spiral is formed, and for negative values the lefthand spiral. | |||
* In [[polar coordinates]] <math>\, r,\varphi</math> the involute of a circle has the parametric equation: | |||
:<math>\, r=a\cdot\sec\alpha=\frac{a}{\cos\alpha}</math> | |||
:<math>\, \varphi = \tan\alpha - \alpha</math> | |||
where <math>\, a</math> is the radius of the circle and <math>\, \alpha</math> is an angle parameter in radians (<math>\alpha\in \mathbb{R}</math>) equal to <math>\, t - \varphi </math> (so <math>\tan\alpha = t</math>). | |||
With that parameter <math>\ \ t\ (\ </math> with <math>\ \ t=\tan\alpha\ ;\ \ t\in \mathbb{R}\ )</math> it can be written in the form: | |||
: <math>\, r = a\cdot \sqrt{1+\ t^2}</math> | |||
: <math>\, \varphi=\ t-\arctan(\ t)</math>. | |||
====Curve length==== | |||
The arc length of the above curve for <math>\ \quad0\le t\le t_1\quad</math> is | |||
::<math>\ L = \frac{a}{2}\cdot t_1^2 </math> | |||
====Application==== | |||
[[Leonhard Euler]] proposed to use the involute of the circle for the shape of the teeth of toothwheel [[gear]], a design which is the prevailing one in current use, called [[involute gear]]. | |||
===Involute of a catenary=== | |||
[[Image:Involute.gif|thumb|500px|right|The involute of a [[catenary]], a [[tractrix]].]] | |||
The involute of a [[catenary]] through its [[vertex (curve)|vertex]] is a [[tractrix]]. In [[cartesian coordinates]] the curve follows: | |||
<math>x=t-\mathrm{tanh}(t)\,</math> | |||
<math>y=\mathrm{sech}(t)\ =\ \frac{1}{\mathrm{cosh}(t)}</math> | |||
Where: ''t'' is a parameter and [[sech]] is the hyperbolic secant (1/cosh(t)) | |||
'''''Derivative''''' | |||
With <math>r(s)=(\sinh^{-1}(s),\cosh(\sinh^{-1}(s)))\,</math> | |||
we have <math>r^\prime(s)=(1,s)/\sqrt{1+s^2}\,</math> | |||
and <math>r(t)-tr^\prime(t)=(\sinh^{-1}(t)-t/\sqrt{1+t^2},1/\sqrt{1+t^2})</math>. | |||
Substitute <math>t=\sqrt{1-y^2}/y</math> | |||
to get <math>({\rm sech}^{-1}(y)-\sqrt{1-y^2},y)</math>. | |||
===Involute of a cycloid=== | |||
''One'' involute of a [[cycloid]] is a [[congruence (geometry)|congruent]] cycloid. In [[cartesian coordinates]] the curve follows: | |||
:<math>x=r(t-\sin(t))\,</math> | |||
:<math>y=r(1-\cos(t))\,</math> | |||
Where ''t'' is the angle and ''r'' is the [[radius]] | |||
==Application== | |||
The involute has some properties that makes it extremely important to the [[gear]] industry: If two intermeshed gears have teeth with the profile-shape of involutes (rather than, for example, a "classic" triangular shape), they form an [[involute gear]] system. Their relative rates of rotation are constant while the teeth are engaged, and also, the gears always make contact along a single steady line of force. With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern gear teeth bear the involute shape. | |||
The involute of a circle is also an important shape in [[gas compressor|gas compressing]], as a [[scroll compressor]] can be built based on this shape. Scroll compressors make less sound than conventional compressors, and have proven to be quite [[mechanical efficiency|efficient]]. | |||
==See also== | |||
* [[Evolute]] | |||
* [[Scroll compressor]] | |||
* [[Involute gear]] | |||
==References== | |||
{{reflist}} | |||
==External links== | |||
* [http://mathworld.wolfram.com/Involute.html Mathworld] | |||
* [http://link.springer.com/article/10.1007%2Fs12045-013-0106-3] Application of the involute to gear teeth - a short historical account | |||
{{Differential transforms of plane curves}} | |||
[[Category:Curves]] | |||
[[Category:Differential geometry]] | |||
Revision as of 11:36, 31 January 2014
In the differential geometry of curves, an involute (also known as evolvent) is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight line containing the generating point. For example, an involute approximates the path followed by a tetherball as the connecting tether is wound around the center pole. If the center pole has a circular cross-section, then the curve is an involute of a circle.
Alternatively, another way to construct the involute of a curve is to replace the taut string by a line segment that is tangent to the curve on one end, while the other end traces out the involute. The length of the line segment is changed by an amount equal to the arc length traversed by the tangent point as it moves along the curve.
The evolute of an involute is the original curve, less portions of zero or undefined curvature. Compare Media:Evolute2.gif and Media:Involute.gif
If the function is a natural parametrization of the curve (i.e., for all s), then : parametrizes the involute.
The notions of the involute and evolute of a curve were introduced by Christiaan Huygens in his work titled Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae (1673).[1]
Parametric curve
Equations of an involute curve for a parametrically defined function ( x(t), y(t) ) are:
Examples
Involute of a circle

unwinding a string

The involute of a circle resembles, but is not, an Archimedean spiral.
Its successive turns are parallel curves with constant separation distance, a property which is often (inaccurately) ascribed to the Archimedean spiral.
- In Cartesian coordinates the involute of a circle has the parametric equation:
where is the radius of the circle and is an angle parameter in radians () where for positive values of the angle parameter the righthand spiral is formed, and for negative values the lefthand spiral.
- In polar coordinates the involute of a circle has the parametric equation:
where is the radius of the circle and is an angle parameter in radians () equal to (so ).
With that parameter with it can be written in the form:
Curve length
The arc length of the above curve for is
Application
Leonhard Euler proposed to use the involute of the circle for the shape of the teeth of toothwheel gear, a design which is the prevailing one in current use, called involute gear.
Involute of a catenary
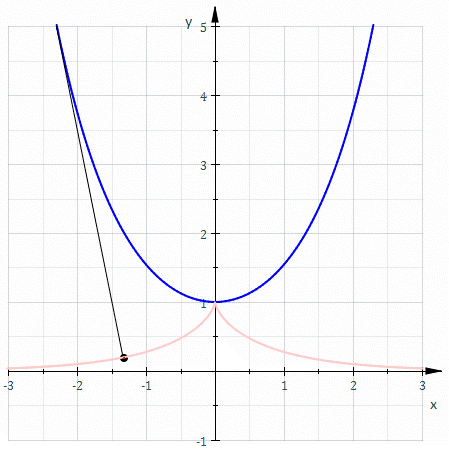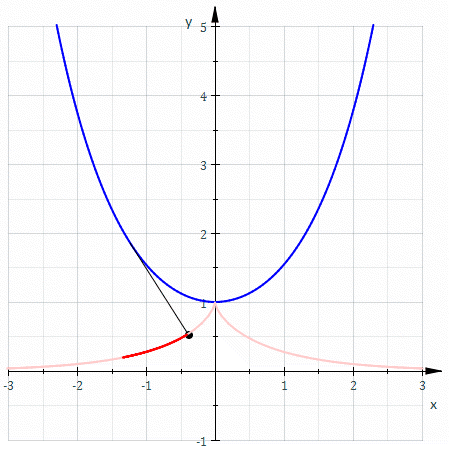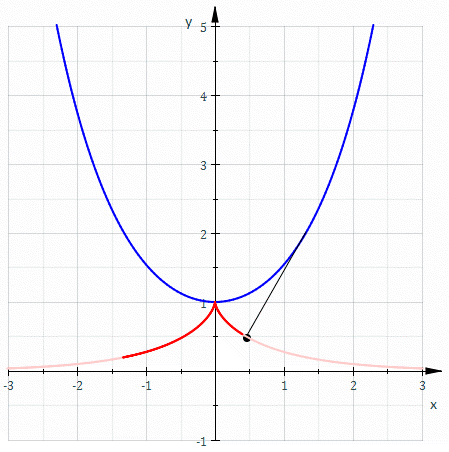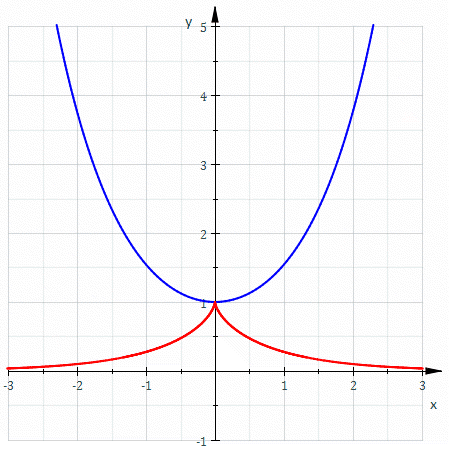
The involute of a catenary through its vertex is a tractrix. In cartesian coordinates the curve follows:
Where: t is a parameter and sech is the hyperbolic secant (1/cosh(t))
Derivative
Involute of a cycloid
One involute of a cycloid is a congruent cycloid. In cartesian coordinates the curve follows:
Where t is the angle and r is the radius
Application
The involute has some properties that makes it extremely important to the gear industry: If two intermeshed gears have teeth with the profile-shape of involutes (rather than, for example, a "classic" triangular shape), they form an involute gear system. Their relative rates of rotation are constant while the teeth are engaged, and also, the gears always make contact along a single steady line of force. With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern gear teeth bear the involute shape.
The involute of a circle is also an important shape in gas compressing, as a scroll compressor can be built based on this shape. Scroll compressors make less sound than conventional compressors, and have proven to be quite efficient.
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
Template:Differential transforms of plane curves
- ↑ John McCleary – Geometry from a Differentiable Viewpoint / Cambridge University Press, 1995 / pg. 73



![{\displaystyle X[x,y]=x-{\frac {x'}{\sqrt {x'^{2}+y'^{2}}}}\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\operatorname {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27a90b6b1d97fa3445493e5be4458ebd552ebac8)
![{\displaystyle Y[x,y]=y-{\frac {y'}{\sqrt {x'^{2}+y'^{2}}}}\int _{a}^{t}{\sqrt {x'^{2}+y'^{2}}}\operatorname {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af6c7aec25660a5c494abd2fb2b7cbedcf599a0f)


























