Ultralimit: Difference between revisions
spacing in formula |
→Limit of a sequence of points with respect to an ultrafilter: Removed redunant "Hausdorff" criterion for a metric space. |
||
| Line 1: | Line 1: | ||
The [[directional derivative|derivatives]] of [[Scalar (mathematics)|scalars]], [[Euclidean vector|vectors]], and second-order [[tensor]]s with respect to second-order tensors are of considerable use in [[continuum mechanics]]. These derivatives are used in the theories of [[nonlinear elasticity]] and [[plasticity (physics)|plasticity]], particularly in the design of [[algorithms]] for [[numerical simulation]]s.<ref name=Simo98>J. C. Simo and T. J. R. Hughes, 1998, ''Computational Inelasticity'', Springer</ref> | |||
The [[directional derivative]] provides a systematic way of finding these derivatives.<ref name=Marsden00>J. E. Marsden and T. J. R. Hughes, 2000, ''Mathematical Foundations of Elasticity'', Dover.</ref> | |||
== Derivatives with respect to vectors and second-order tensors == | |||
The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken. | |||
===Derivatives of scalar valued functions of vectors=== | |||
Let ''f''('''v''') be a real valued function of the vector '''v'''. Then the derivative of ''f''('''v''') with respect to '''v''' (or at '''v''') in the direction '''u''' is the '''vector''' defined as | |||
:<math>\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = Df(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~f(\mathbf{v} + \alpha~\mathbf{u})\right]_{\alpha = 0}</math> | |||
for all vectors '''u'''. | |||
''Properties:'' | |||
1) If <math>f(\mathbf{v}) = f_1(\mathbf{v}) + f_2(\mathbf{v})</math> then <math>\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial f_1}{\partial \mathbf{v}} + \frac{\partial f_2}{\partial \mathbf{v}}\right)\cdot\mathbf{u}</math> | |||
2) If <math>f(\mathbf{v}) = f_1(\mathbf{v})~ f_2(\mathbf{v})</math> then <math>\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial f_1}{\partial \mathbf{v}} \cdot \mathbf{u} \right)~f_2(\mathbf{v}) + f_1(\mathbf{v})~\left(\frac{\partial f_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)</math> | |||
3) If <math>f(\mathbf{v}) = f_1(f_2(\mathbf{v}))</math> then <math>\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \frac{\partial f_1}{\partial f_2}~\frac{\partial f_2}{\partial \mathbf{v}}\cdot\mathbf{u}</math> | |||
===Derivatives of vector valued functions of vectors=== | |||
Let '''f'''('''v''') be a vector valued function of the vector '''v'''. Then the derivative of '''f'''('''v''') with respect to '''v''' (or at '''v''') in the direction '''u''' is the ''' second order tensor''' defined as | |||
:<math> \frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = D\mathbf{f}(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~\mathbf{f}(\mathbf{v} + \alpha~\mathbf{u} ) \right]_{\alpha = 0}</math> | |||
for all vectors '''u'''. | |||
:'''Properties:''' | |||
:1) If <math>\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v}) + \mathbf{f}_2(\mathbf{v})</math> then <math>\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial \mathbf{f}_1}{\partial \mathbf{v}} + \frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\right)\cdot\mathbf{u} </math> | |||
:2) If <math>\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v})\times\mathbf{f}_2(\mathbf{v})</math> then <math>\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial \mathbf{f}_1}{\partial \mathbf{v}}\cdot\mathbf{u}\right)\times\mathbf{f}_2(\mathbf{v}) + \mathbf{f}_1(\mathbf{v})\times\left(\frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)</math> | |||
:3) If <math>\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{f}_2(\mathbf{v}))</math> then <math>\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \frac{\partial \mathbf{f}_1}{\partial \mathbf{f}_2}\cdot\left(\frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)</math> | |||
===Derivatives of scalar valued functions of second-order tensors=== | |||
Let <math>f(\boldsymbol{S})</math> be a real valued function of the second order tensor <math>\boldsymbol{S}</math>. Then the derivative of <math>f(\boldsymbol{S})</math> with respect to <math>\boldsymbol{S}</math> (or at <math>\boldsymbol{S}</math>) in the direction <math>\boldsymbol{T}</math> is the ''' second order tensor''' defined as | |||
:<math>\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = Df(\boldsymbol{S})[\boldsymbol{T}] = \left[\frac{d }{d \alpha}~f(\boldsymbol{S} + \alpha~\boldsymbol{T})\right]_{\alpha = 0}</math> | |||
for all second order tensors <math>\boldsymbol{T}</math>. | |||
:'''Properties:''' | |||
:1) If <math>f(\boldsymbol{S}) = f_1(\boldsymbol{S}) + f_2(\boldsymbol{S})</math> then <math> \frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial f_1}{\partial \boldsymbol{S}} + \frac{\partial f_2}{\partial \boldsymbol{S}}\right):\boldsymbol{T} </math> | |||
:2) If <math>f(\boldsymbol{S}) = f_1(\boldsymbol{S})~ f_2(\boldsymbol{S})</math> then <math> \frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial f_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)~f_2(\boldsymbol{S}) + f_1(\boldsymbol{S})~\left(\frac{\partial f_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right) </math> | |||
:3) If <math>f(\boldsymbol{S}) = f_1(f_2(\boldsymbol{S}))</math> then <math> \frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial f_1}{\partial f_2}~\left(\frac{\partial f_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right) </math> | |||
===Derivatives of tensor valued functions of second-order tensors=== | |||
Let <math>\boldsymbol{F}(\boldsymbol{S})</math> be a second order tensor valued function of the second order tensor <math>\boldsymbol{S}</math>. Then the derivative of <math>\boldsymbol{F}(\boldsymbol{S})</math> with respect to <math>\boldsymbol{S}</math> (or at <math>\boldsymbol{S}</math>) in the direction <math>\boldsymbol{T}</math> is the ''' fourth order tensor''' defined as | |||
:<math>\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = D\boldsymbol{F}(\boldsymbol{S})[\boldsymbol{T}] = \left[\frac{d }{d \alpha}~\boldsymbol{F}(\boldsymbol{S} + \alpha~\boldsymbol{T})\right]_{\alpha = 0}</math> | |||
for all second order tensors <math>\boldsymbol{T}</math>. | |||
:'''Properties:''' | |||
:1) If <math>\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{S}) + \boldsymbol{F}_2(\boldsymbol{S})</math> then <math> \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}} + \frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}\right):\boldsymbol{T} </math> | |||
:2) If <math>\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{S})\cdot\boldsymbol{F}_2(\boldsymbol{S})</math> then <math> \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)\cdot\boldsymbol{F}_2(\boldsymbol{S}) + \boldsymbol{F}_1 (\boldsymbol{S}) \cdot\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right) </math> | |||
:3) If <math>\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{F}_2(\boldsymbol{S}))</math> then <math> \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{F}_2}:\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right) </math> | |||
:4) If <math>f(\boldsymbol{S}) = f_1(\boldsymbol{F}_2(\boldsymbol{S}))</math> then <math> \frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial f_1}{\partial \boldsymbol{F}_2}:\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right) </math> | |||
== Gradient of a tensor field == | |||
The [[gradient]], <math>\boldsymbol{\nabla}\boldsymbol{T}</math>, of a tensor field <math>\boldsymbol{T}(\mathbf{x})</math> in the direction of an arbitrary constant vector '''c''' is defined as: | |||
:<math> \boldsymbol{\nabla}\boldsymbol{T}\cdot\mathbf{c} = \left.\cfrac{d}{d\alpha}~\boldsymbol{T}(\mathbf{x}+\alpha\mathbf{c})\right|_{\alpha=0}</math> | |||
The gradient of a tensor field of order ''n'' is a tensor field of order ''n''+1. | |||
=== Cartesian coordinates === | |||
{{Einstein_summation_convention}} | |||
If <math>\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3</math> are the basis vectors in a [[Cartesian coordinate]] system, with coordinates of points denoted by (<math>x_1, x_2, x_3</math>), then the gradient of the tensor field <math>\boldsymbol{T}</math> is given by | |||
:<math> \boldsymbol{\nabla}\boldsymbol{T} = \cfrac{\partial{\boldsymbol{T}}}{\partial x_i}\otimes\mathbf{e}_i </math> | |||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" | |||
!Proof | |||
|- | |||
| | |||
The vectors '''x''' and '''c''' can be written as <math> \mathbf{x} = x_i~\mathbf{e}_i </math> and <math>\mathbf{c} = c_i~\mathbf{e}_i </math> . Let '''y''' := '''x''' + α'''c'''. In that case the gradient is given by | |||
:<math> | |||
\begin{align} | |||
\boldsymbol{\nabla}\boldsymbol{T}\cdot\mathbf{c} & = \left.\cfrac{d}{d\alpha}~\boldsymbol{T}(x_1+\alpha c_1, x_2 + \alpha c_2, x_3 + \alpha c_3)\right|_{\alpha=0} \equiv \left.\cfrac{d}{d\alpha}~\boldsymbol{T}(y_1, y_2, y_3)\right|_{\alpha=0} \\ | |||
& = \left [\cfrac{\partial{\boldsymbol{T}}}{\partial y_1}~\cfrac{\partial y_1}{\partial \alpha} + \cfrac{\partial{\boldsymbol{T}}}{\partial y_2}~\cfrac{\partial y_2}{\partial \alpha} + | |||
\cfrac{\partial{\boldsymbol{T}}}{\partial y_3}~\cfrac{\partial y_3}{\partial \alpha} \right]_{\alpha=0} = | |||
\left [\cfrac{\partial{\boldsymbol{T}}}{\partial y_1}~c_1 + \cfrac{\partial{\boldsymbol{T}}}{\partial y_2}~c_2 + | |||
\cfrac{\partial{\boldsymbol{T}}}{\partial y_3}~c_3 \right]_{\alpha=0} \\ | |||
& = \cfrac{\partial{\boldsymbol{T}}}{\partial x_1}~c_1 + \cfrac{\partial{\boldsymbol{T}}}{\partial x_2}~c_2 + | |||
\cfrac{\partial{\boldsymbol{T}}}{\partial x_3}~c_3 \equiv \cfrac{\partial{\boldsymbol{T}}}{\partial x_i}~c_i = \cfrac{\partial{\boldsymbol{T}}}{\partial x_i}~(\mathbf{e}_i\cdot\mathbf{c}) | |||
= \left[\cfrac{\partial{\boldsymbol{T}}}{\partial x_i}\otimes\mathbf{e}_i\right]\cdot\mathbf{c} \qquad \square | |||
\end{align} | |||
</math> | |||
|} | |||
Since the basis vectors do not vary in a Cartesian coordinate system we have the following relations for the gradients of a scalar field <math>\phi</math>, a vector field '''v''', and a second-order tensor field <math>\boldsymbol{S}</math>. | |||
:<math> \begin{align} | |||
\boldsymbol{\nabla}\phi & = \cfrac{\partial\phi}{\partial x_i}~\mathbf{e}_i \\ | |||
\boldsymbol{\nabla}\mathbf{v} & = \cfrac{\partial (v_j \mathbf{e}_j)}{\partial x_i}\otimes\mathbf{e}_i = \cfrac{\partial v_j}{\partial x_i}~\mathbf{e}_j\otimes\mathbf{e}_i\\ | |||
\boldsymbol{\nabla}\boldsymbol{S} & = \cfrac{\partial (S_{jk} \mathbf{e}_j\otimes\mathbf{e}_k)}{\partial x_i}\otimes\mathbf{e}_i = \cfrac{\partial S_{jk}}{\partial x_i}~\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_i | |||
\end{align} | |||
</math> | |||
=== Curvilinear coordinates === | |||
{{main|Curvilinear coordinates}} | |||
{{Einstein_summation_convention}} | |||
If <math>\mathbf{g}^1,\mathbf{g}^2,\mathbf{g}^3</math> are the [[Covariance and contravariance of vectors|contravariant]] [[basis vector]]s in a [[curvilinear coordinates|curvilinear coordinate]] system, with coordinates of points denoted by (<math>\xi^1, \xi^2, \xi^3</math>), then the gradient of the tensor field <math>\boldsymbol{T}</math> is given by (see <ref>Ogden, R. W., 2000, '''Nonlinear Elastic Deformations''', Dover.</ref> for a proof.) | |||
:<math> | |||
\boldsymbol{\nabla}\boldsymbol{T} = \cfrac{\partial{\boldsymbol{T}}}{\partial \xi^i}\otimes\mathbf{g}^i | |||
</math> | |||
From this definition we have the following relations for the gradients of a scalar field <math>\phi</math>, a vector field '''v''', and a second-order tensor field <math>\boldsymbol{S}</math>. | |||
:<math>\begin{align} | |||
\boldsymbol{\nabla}\phi & = \cfrac{\partial\phi}{\partial \xi^i}~\mathbf{g}^i \\ | |||
\boldsymbol{\nabla}\mathbf{v} & = \cfrac{\partial (v^j \mathbf{g}_j)}{\partial \xi^i}\otimes\mathbf{g}^i | |||
= \left(\cfrac{\partial v^j}{\partial \xi^i} + v^k~\Gamma_{ik}^j\right)~\mathbf{g}_j\otimes\mathbf{g}^i | |||
= \left(\cfrac{\partial v_j}{\partial \xi^i} - v_k~\Gamma_{ij}^k\right)~\mathbf{g}^j\otimes\mathbf{g}^i\\ | |||
\boldsymbol{\nabla}\boldsymbol{S} & = \cfrac{\partial (S_{jk}~\mathbf{g}^j\otimes\mathbf{g}^k)}{\partial \xi^i}\otimes\mathbf{g}^i | |||
= \left(\cfrac{\partial S_{jk}}{\partial \xi_i}- S_{lk}~\Gamma_{ij}^l - S_{jl}~\Gamma_{ik}^l\right)~\mathbf{g}^j\otimes\mathbf{g}^k\otimes\mathbf{g}^i | |||
\end{align} </math> | |||
where the [[Christoffel symbol]] <math>\Gamma_{ij}^k</math> is defined using | |||
:<math> \Gamma_{ij}^k~\mathbf{g}_k = \cfrac{\partial \mathbf{g}_i}{\partial \xi^j} \quad \implies \quad | |||
\Gamma_{ij}^k = \cfrac{\partial \mathbf{g}_i}{\partial \xi^j}\cdot\mathbf{g}_k = -\mathbf{g}_i\cdot\cfrac{\partial \mathbf{g}^k}{\partial \xi^j} | |||
</math> | |||
==== Cylindrical polar coordinates ==== | |||
In [[cylindrical coordinate]]s, the gradient is given by | |||
:<math>\begin{align} | |||
\boldsymbol{\nabla}\phi &=\cfrac{\partial \phi}{\partial r}~\mathbf{e}_r + \cfrac{1}{r}~\cfrac{\partial \phi}{\partial \theta}~\mathbf{e}_\theta +\cfrac{\partial \phi}{\partial z}~\mathbf{e}_z \\ | |||
\boldsymbol{\nabla}\mathbf{v} &= \cfrac{\partial v_r}{\partial r}~\mathbf{e}_r\otimes\mathbf{e}_r + \cfrac{1}{r}\left(\cfrac{\partial v_r}{\partial \theta} -v_\theta \right)~\mathbf{e}_r \otimes \mathbf{e}_\theta + \cfrac{\partial v_r}{\partial z}~\mathbf{e}_r\otimes\mathbf{e}_z +\cfrac{\partial v_\theta}{\partial r}~\mathbf{e}_\theta\otimes\mathbf{e}_r +\cfrac{1}{r}\left(\cfrac{\partial v_\theta}{\partial \theta} + v_r \right)~\mathbf{e}_\theta\otimes\mathbf{e}_\theta \\ | |||
&\quad + \cfrac{\partial v_\theta}{\partial z}~\mathbf{e}_\theta \otimes\mathbf{e}_z + \cfrac{\partial v_z}{\partial r}~\mathbf{e}_z\otimes\mathbf{e}_r + \cfrac{1}{r}\cfrac{\partial v_z}{\partial \theta}~\mathbf{e}_z \otimes\mathbf{e}_\theta + \cfrac{\partial v_z}{\partial z}~\mathbf{e}_z\otimes\mathbf{e}_z \\ | |||
\boldsymbol{\nabla}\boldsymbol{S} & = \frac{\partial S_{rr}}{\partial r}~\mathbf{e}_r\otimes\mathbf{e}_r\otimes\mathbf{e}_r + \cfrac{1}{r}\left[\frac{\partial S_{rr}}{\partial \theta} - (S_{\theta r}+S_{r\theta})\right]~\mathbf{e}_r\otimes\mathbf{e}_r\otimes\mathbf{e}_\theta + \frac{\partial S_{rr}}{\partial z}~\mathbf{e}_r \otimes \mathbf{e}_r\otimes\mathbf{e}_z + \frac{\partial S_{r\theta}}{\partial r}~\mathbf{e}_r\otimes\mathbf{e}_\theta\otimes\mathbf{e}_r \\ | |||
&\quad+ \cfrac{1}{r}\left[\frac{\partial S_{r\theta}}{\partial \theta} + (S_{rr}-S_{\theta\theta}) \right]~\mathbf{e}_r\otimes\mathbf{e}_\theta\otimes\mathbf{e}_\theta + \frac{\partial S_{r\theta}}{\partial z}~\mathbf{e}_r\otimes\mathbf{e}_\theta\otimes\mathbf{e}_z + \frac{\partial S_{rz}}{\partial r}~\mathbf{e}_r \otimes \mathbf{e}_z \otimes \mathbf{e}_r + \cfrac{1}{r}\left[\frac{\partial S_{rz}}{\partial \theta} -S_{\theta z} \right]~\mathbf{e}_r\otimes\mathbf{e}_z\otimes\mathbf{e}_\theta \\ | |||
&\quad+ \frac{\partial S_{rz}}{\partial z}~\mathbf{e}_r \otimes \mathbf{e}_z\otimes\mathbf{e}_z + \frac{\partial S_{\theta r}}{\partial r}~\mathbf{e}_\theta \otimes \mathbf{e}_r \otimes \mathbf{e}_r + \cfrac{1}{r}\left[\frac{\partial S_{\theta r}}{\partial \theta} + (S_{rr}-S_{\theta\theta}) \right]~\mathbf{e}_\theta\otimes\mathbf{e}_r\otimes\mathbf{e}_\theta + \frac{\partial S_{\theta r}}{\partial z}~\mathbf{e}_\theta\otimes\mathbf{e}_r\otimes\mathbf{e}_z \\ | |||
&\quad+ \frac{\partial S_{\theta\theta}}{\partial r}~\mathbf{e}_\theta\otimes\mathbf{e}_\theta\otimes\mathbf{e}_r +\cfrac{1}{r}\left[\frac{\partial S_{\theta\theta}}{\partial \theta} + (S_{r\theta}+S_{\theta r})\right]~\mathbf{e}_\theta\otimes\mathbf{e}_\theta\otimes\mathbf{e}_\theta + \frac{\partial S_{\theta\theta}}{\partial z}~\mathbf{e}_\theta \otimes \mathbf{e}_\theta \otimes \mathbf{e}_z + \frac{\partial S_{\theta z}}{\partial r}~\mathbf{e}_\theta \otimes \mathbf{e}_z\otimes\mathbf{e}_r \\ | |||
&\quad+ \cfrac{1}{r}\left[\frac{\partial S_{\theta z}}{\partial \theta} + S_{rz} \right]~\mathbf{e}_\theta \otimes\mathbf{e}_z\otimes\mathbf{e}_\theta + \frac{\partial S_{\theta z}}{\partial z}~\mathbf{e}_\theta\otimes\mathbf{e}_z\otimes\mathbf{e}_z + \frac{\partial S_{zr}}{\partial r}~\mathbf{e}_z\otimes\mathbf{e}_r\otimes\mathbf{e}_r + \cfrac{1}{r}\left[\frac{\partial S_{zr}}{\partial \theta} - S_{z\theta} \right]~\mathbf{e}_z \otimes \mathbf{e}_r \otimes\mathbf{e}_\theta \\ | |||
&\quad+ \frac{\partial S_{zr}}{\partial z}~\mathbf{e}_z\otimes\mathbf{e}_r\otimes\mathbf{e}_z + \frac{\partial S_{z\theta}}{\partial r}~\mathbf{e}_z \otimes \mathbf{e}_\theta \otimes \mathbf{e}_r + \cfrac{1}{r}\left[\frac{\partial S_{z\theta}}{\partial \theta} + S_{zr} \right]~\mathbf{e}_z \otimes\mathbf{e}_\theta \otimes \mathbf{e}_\theta + \frac{\partial S_{z\theta}}{\partial z}~\mathbf{e}_z\otimes\mathbf{e}_\theta\otimes\mathbf{e}_z \\ | |||
&\quad+ \frac{\partial S_{zz}}{\partial r}~\mathbf{e}_z\otimes\mathbf{e}_z\otimes\mathbf{e}_r + \cfrac{1}{r}~\frac{\partial S_{zz}}{\partial \theta }~\mathbf{e}_z \otimes \mathbf{e}_z \otimes\mathbf{e}_\theta + \frac{\partial S_{zz}}{\partial z}~\mathbf{e}_z\otimes\mathbf{e}_z\otimes\mathbf{e}_z | |||
\end{align} </math> | |||
== Divergence of a tensor field == | |||
The [[divergence]] of a tensor field <math>\boldsymbol{T}(\mathbf{x})</math> is defined using the recursive relation | |||
:<math> | |||
(\boldsymbol{\nabla}\cdot\boldsymbol{T})\cdot\mathbf{c} = \boldsymbol{\nabla}\cdot(\mathbf{c}\cdot\boldsymbol{T}) ~;\qquad\boldsymbol{\nabla}\cdot\mathbf{v} = \text{tr}(\boldsymbol{\nabla}\mathbf{v}) | |||
</math> | |||
where '''c''' is an arbitrary constant vector and '''v''' is a vector field. If <math>\boldsymbol{T}</math> is a tensor field of order ''n'' > 1 then the divergence of the field is a tensor of order ''n''−1. | |||
=== Cartesian coordinates === | |||
{{Einstein_summation_convention}} | |||
In a Cartesian coordinate system we have the following relations for a vector field '''v''' and a second-order tensor field <math>\boldsymbol{S}</math>. | |||
:<math>\begin{align} | |||
\boldsymbol{\nabla}\cdot\mathbf{v} &= \cfrac{\partial v_i}{\partial x_i} \\ | |||
\boldsymbol{\nabla}\cdot\boldsymbol{S} &= \cfrac{\partial S_{ki}}{\partial x_i}~\mathbf{e}_k | |||
\end{align}</math> | |||
Note that in the case of the second-order tensor field, we have<ref>http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_1_Vectors_Tensors/Vectors_Tensors_14_Tensor_Calculus.pdf</ref> | |||
:<math>\boldsymbol{\nabla}\cdot\boldsymbol{S} \neq \operatorname{div}\boldsymbol{S} = \boldsymbol{\nabla}\cdot\boldsymbol{S}^\mathrm{T}.</math> | |||
=== Curvilinear coordinates === | |||
{{main|Curvilinear coordinates}} | |||
{{Einstein_summation_convention}} | |||
In curvilinear coordinates, the divergences of a vector field '''v''' and a second-order tensor field <math>\boldsymbol{S}</math> are | |||
:<math> | |||
\begin{align} | |||
\boldsymbol{\nabla}\cdot\mathbf{v} & | |||
= \left(\cfrac{\partial v^i}{\partial \xi^i} + v^k~\Gamma_{ik}^i\right)\\ | |||
\boldsymbol{\nabla}\cdot\boldsymbol{S} & | |||
= \left(\cfrac{\partial S_{ik}}{\partial \xi_i}- S_{lk}~\Gamma_{ii}^l - S_{il}~\Gamma_{ik}^l\right)~\mathbf{g}^k | |||
\end{align} | |||
</math> | |||
==== Cylindrical polar coordinates ==== | |||
In [[cylindrical coordinates|cylindrical polar coordinates]] | |||
:<math> | |||
\begin{align} | |||
\boldsymbol{\nabla}\cdot\mathbf{v} & | |||
= \cfrac{\partial v_r}{\partial r} + | |||
\cfrac{1}{r}\left(\cfrac{\partial v_\theta}{\partial \theta} + v_r \right) | |||
+ \cfrac{\partial v_z}{\partial z}\\ | |||
\boldsymbol{\nabla}\cdot\boldsymbol{S} & | |||
= \frac{\partial S_{rr}}{\partial r}~\mathbf{e}_r | |||
+ \frac{\partial S_{r\theta}}{\partial r}~\mathbf{e}_\theta | |||
+ \frac{\partial S_{rz}}{\partial r}~\mathbf{e}_z \\ | |||
& + | |||
\cfrac{1}{r}\left[\frac{\partial S_{\theta r}}{\partial \theta} + (S_{rr}-S_{\theta\theta})\right]~\mathbf{e}_r + | |||
\cfrac{1}{r}\left[\frac{\partial S_{\theta\theta}}{\partial \theta} + (S_{r\theta}+S_{\theta r})\right]~\mathbf{e}_\theta +\cfrac{1}{r}\left[\frac{\partial S_{\theta z}}{\partial \theta} + S_{rz}\right]~\mathbf{e}_z \\ | |||
& + | |||
\frac{\partial S_{zr}}{\partial z}~\mathbf{e}_r + | |||
\frac{\partial S_{z\theta}}{\partial z}~\mathbf{e}_\theta + | |||
\frac{\partial S_{zz}}{\partial z}~\mathbf{e}_z | |||
\end{align} | |||
</math> | |||
== Curl of a tensor field == | |||
The [[curl (mathematics)|curl]] of an order-''n'' > 1 tensor field <math>\boldsymbol{T}(\mathbf{x})</math> is also defined using the recursive relation | |||
:<math>(\boldsymbol{\nabla}\times\boldsymbol{T})\cdot\mathbf{c} = \boldsymbol{\nabla}\times(\mathbf{c}\cdot\boldsymbol{T}) ~;\qquad (\boldsymbol{\nabla}\times\mathbf{v})\cdot\mathbf{c} = \boldsymbol{\nabla}\cdot(\mathbf{v}\times\mathbf{c})</math> | |||
where '''c''' is an arbitrary constant vector and '''v''' is a vector field. | |||
=== Curl of a first-order tensor (vector) field === | |||
Consider a vector field '''v''' and an arbitrary constant vector '''c'''. In index notation, the cross product is given by | |||
:<math> | |||
\mathbf{v} \times \mathbf{c} = e_{ijk}~v_j~c_k~\mathbf{e}_i | |||
</math> | |||
where <math>e_{ijk}</math> is the [[permutation symbol]]. Then, | |||
:<math> | |||
\boldsymbol{\nabla}\cdot(\mathbf{v} \times \mathbf{c}) = e_{ijk}~v_{j,i}~c_k = (e_{ijk}~v_{j,i}~\mathbf{e}_k)\cdot\mathbf{c} = (\boldsymbol{\nabla}\times\mathbf{v})\cdot\mathbf{c} | |||
</math> | |||
Therefore | |||
:<math>\boldsymbol{\nabla}\times\mathbf{v} = e_{ijk}~v_{j,i}~\mathbf{e}_k</math> | |||
=== Curl of a second-order tensor field === | |||
For a second-order tensor <math>\boldsymbol{S}</math> | |||
:<math> \mathbf{c}\cdot\boldsymbol{S} = c_m~S_{mj}~\mathbf{e}_j | |||
</math> | |||
Hence, using the definition of the curl of a first-order tensor field, | |||
:<math> \boldsymbol{\nabla}\times(\mathbf{c}\cdot\boldsymbol{S}) = e_{ijk}~c_m~S_{mj,i}~\mathbf{e}_k = (e_{ijk}~S_{mj,i}~\mathbf{e}_k\otimes\mathbf{e}_m)\cdot\mathbf{c} = (\boldsymbol{\nabla}\times\boldsymbol{S})\cdot\mathbf{c} | |||
</math> | |||
Therefore, we have | |||
:<math> \boldsymbol{\nabla}\times\boldsymbol{S} = e_{ijk}~S_{mj,i}~\mathbf{e}_k\otimes\mathbf{e}_m | |||
</math> | |||
=== Identities involving the curl of a tensor field === | |||
The most commonly used identity involving the curl of a tensor field, <math>\boldsymbol{T}</math>, is | |||
:<math> | |||
\boldsymbol{\nabla}\times(\boldsymbol{\nabla}\boldsymbol{T}) = \boldsymbol{0} | |||
</math> | |||
This identity hold for tensor fields of all orders. For the important case of a second-order tensor, <math>\boldsymbol{S}</math>, this identity implies that | |||
:<math> | |||
\boldsymbol{\nabla}\times\boldsymbol{S} = \boldsymbol{0} \quad \implies \quad S_{mi,j} - S_{mj,i} = 0 | |||
</math> | |||
==Derivative of the determinant of a second-order tensor== | |||
The derivative of the determinant of a second order tensor <math>\boldsymbol{A}</math> is given by | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}}\det(\boldsymbol{A}) = \det(\boldsymbol{A})~[\boldsymbol{A}^{-1}]^T ~. | |||
</math> | |||
In an orthonormal basis, the components of <math>\boldsymbol{A}</math> can be written as a matrix '''A'''. In that case, the right hand side corresponds the cofactors of the matrix. | |||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" | |||
!Proof | |||
|- | |||
| | |||
Let <math>\boldsymbol{A}</math> be a second order tensor and let <math>f(\boldsymbol{A}) = \det(\boldsymbol{A})</math>. Then, from the definition of the derivative of a scalar valued function of a tensor, we have | |||
:<math>\begin{align} | |||
\frac{\partial f}{\partial \boldsymbol{A}}:\boldsymbol{T} & = \left.\cfrac{d}{d\alpha} \det(\boldsymbol{A} + \alpha~\boldsymbol{T}) \right|_{\alpha=0} \\ | |||
& = \left.\cfrac{d}{d\alpha} \det\left[\alpha~\boldsymbol{A}\left(\cfrac{1}{\alpha}~\boldsymbol{\mathit{I}} + \boldsymbol{A}^{-1}\cdot\boldsymbol{T}\right) \right] \right|_{\alpha=0} \\ | |||
& = \left.\cfrac{d}{d\alpha} \left[\alpha^3~\det(\boldsymbol{A})~\det\left(\cfrac{1}{\alpha}~\boldsymbol{\mathit{I}} + \boldsymbol{A}^{-1} \cdot \boldsymbol{T}\right)\right]\right|_{\alpha=0}. | |||
\end{align}</math> | |||
Recall that we can expand the determinant of a tensor in the form of a characteristic equation in terms of the invariants <math>I_1,I_2,I_3</math> using (note the sign of λ) | |||
:<math> \det(\lambda~\boldsymbol{\mathit{I}} + \boldsymbol{A}) = \lambda^3 + I_1(\boldsymbol{A})~\lambda^2 + I_2(\boldsymbol{A})~\lambda + I_3(\boldsymbol{A}).</math> | |||
Using this expansion we can write | |||
:<math> \begin{align} | |||
\frac{\partial f}{\partial \boldsymbol{A}}:\boldsymbol{T} | |||
& = \left.\cfrac{d}{d\alpha} \left[\alpha^3~\det(\boldsymbol{A})~ | |||
\left(\cfrac{1}{\alpha^3} + I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\cfrac{1}{\alpha^2} + | |||
I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\cfrac{1}{\alpha} + I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})\right) | |||
\right] \right|_{\alpha=0} \\ | |||
& = \left.\det(\boldsymbol{A})~\cfrac{d}{d\alpha} \left[ | |||
1 + I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha + | |||
I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^2 + I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^3 | |||
\right] \right|_{\alpha=0} \\ | |||
& = \left.\det(\boldsymbol{A})~\left[I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T}) + | |||
2~I_2(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha + 3~I_3(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})~\alpha^2 | |||
\right] \right|_{\alpha=0} \\ | |||
& = \det(\boldsymbol{A})~I_1(\boldsymbol{A}^{-1}\cdot\boldsymbol{T}) ~. | |||
\end{align} | |||
</math> | |||
Recall that the invariant <math>I_1</math> is given by | |||
:<math> I_1(\boldsymbol{A}) = \text{tr}{\boldsymbol{A}}.</math> | |||
Hence, | |||
:<math>\frac{\partial f}{\partial \boldsymbol{A}}:\boldsymbol{T} = \det(\boldsymbol{A})~\text{tr}(\boldsymbol{A}^{-1}\cdot\boldsymbol{T})= \det(\boldsymbol{A})~[\boldsymbol{A}^{-1}]^T : \boldsymbol{T}.</math> | |||
Invoking the arbitrariness of <math>\boldsymbol{T}</math> we then have | |||
:<math> | |||
\frac{\partial f}{\partial \boldsymbol{A}} = \det(\boldsymbol{A})~[\boldsymbol{A}^{-1}]^T ~. | |||
</math> | |||
|} | |||
==Derivatives of the invariants of a second-order tensor== | |||
The principal invariants of a second order tensor are | |||
:<math> | |||
\begin{align} | |||
I_1(\boldsymbol{A}) & = \text{tr}{\boldsymbol{A}} \\ | |||
I_2(\boldsymbol{A}) & = \frac{1}{2} \left[ (\text{tr}{\boldsymbol{A}})^2 - \text{tr}{\boldsymbol{A}^2} \right] \\ | |||
I_3(\boldsymbol{A}) & = \det(\boldsymbol{A}) | |||
\end{align} | |||
</math> | |||
The derivatives of these three invariants with respect to <math>\boldsymbol{A}</math> are | |||
:<math> | |||
\begin{align} | |||
\frac{\partial I_1}{\partial \boldsymbol{A}} & = \boldsymbol{\mathit{1}} \\ | |||
\frac{\partial I_2}{\partial \boldsymbol{A}} & = I_1~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T \\ | |||
\frac{\partial I_3}{\partial \boldsymbol{A}} & = \det(\boldsymbol{A})~[\boldsymbol{A}^{-1}]^T | |||
= I_2~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T~(I_1~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T) | |||
= (\boldsymbol{A}^2 - I_1~\boldsymbol{A} + I_2~\boldsymbol{\mathit{1}})^T | |||
\end{align} | |||
</math> | |||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" | |||
!Proof | |||
|- | |||
|From the derivative of the determinant we know that | |||
:<math> | |||
\frac{\partial I_3}{\partial \boldsymbol{A}} = \det(\boldsymbol{A})~[\boldsymbol{A}^{-1}]^T ~. | |||
</math> | |||
For the derivatives of the other two invariants, let us go back to the characteristic equation | |||
:<math> | |||
\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A}) = | |||
\lambda^3 + I_1(\boldsymbol{A})~\lambda^2 + I_2(\boldsymbol{A})~\lambda + I_3(\boldsymbol{A}) ~. | |||
</math> | |||
Using the same approach as for the determinant of a tensor, we can show that | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}}\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A}) = | |||
\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A})~[(\lambda~\boldsymbol{\mathit{1}}+\boldsymbol{A})^{-1}]^T ~. | |||
</math> | |||
Now the left hand side can be expanded as | |||
:<math> | |||
\begin{align} | |||
\frac{\partial }{\partial \boldsymbol{A}}\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A}) & = | |||
\frac{\partial }{\partial \boldsymbol{A}}\left[ | |||
\lambda^3 + I_1(\boldsymbol{A})~\lambda^2 + I_2(\boldsymbol{A})~\lambda + I_3(\boldsymbol{A}) \right] \\ | |||
& = | |||
\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}}~. | |||
\end{align} | |||
</math> | |||
Hence | |||
:<math> | |||
\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}} = | |||
\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A})~[(\lambda~\boldsymbol{\mathit{1}}+\boldsymbol{A})^{-1}]^T | |||
</math> | |||
or, | |||
:<math> | |||
(\lambda~\boldsymbol{\mathit{1}}+\boldsymbol{A})^T\cdot\left[ | |||
\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}}\right] = | |||
\det(\lambda~\boldsymbol{\mathit{1}} + \boldsymbol{A})~\boldsymbol{\mathit{1}} ~. | |||
</math> | |||
Expanding the right hand side and separating terms on the left hand side gives | |||
:<math> | |||
(\lambda~\boldsymbol{\mathit{1}} +\boldsymbol{A}^T)\cdot\left[ | |||
\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}}\right] = | |||
\left[\lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right] | |||
\boldsymbol{\mathit{1}} | |||
</math> | |||
or, | |||
:<math> | |||
\begin{align} | |||
\left[\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^3 \right.& | |||
\left.+ \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda^2 + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}}~\lambda\right]\boldsymbol{\mathit{1}} + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}} \\ | |||
& = | |||
\left[\lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right] | |||
\boldsymbol{\mathit{1}} ~. | |||
\end{align} | |||
</math> | |||
If we define <math>I_0 := 1</math> and <math>I_4 := 0</math>, we can write the above as | |||
:<math> | |||
\begin{align} | |||
\left[\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^3 \right.& | |||
\left.+ \frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda^2 + | |||
\frac{\partial I_3}{\partial \boldsymbol{A}}~\lambda + \frac{\partial I_4}{\partial \boldsymbol{A}}\right]\boldsymbol{\mathit{1}} + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_0}{\partial \boldsymbol{A}}~\lambda^3 + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_1}{\partial \boldsymbol{A}}~\lambda^2 + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}}~\lambda + | |||
\boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}} \\ | |||
&= | |||
\left[I_0~\lambda^3 + I_1~\lambda^2 + I_2~\lambda + I_3\right] | |||
\boldsymbol{\mathit{1}} ~. | |||
\end{align} | |||
</math> | |||
Collecting terms containing various powers of λ, we get | |||
:<math> | |||
\begin{align} | |||
\lambda^3&\left(I_0~\boldsymbol{\mathit{1}} - \frac{\partial I_1}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - | |||
\boldsymbol{A}^T\cdot\frac{\partial I_0}{\partial \boldsymbol{A}}\right) + | |||
\lambda^2\left(I_1~\boldsymbol{\mathit{1}} - \frac{\partial I_2}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - | |||
\boldsymbol{A}^T\cdot\frac{\partial I_1}{\partial \boldsymbol{A}}\right) + \\ | |||
&\qquad \qquad\lambda\left(I_2~\boldsymbol{\mathit{1}} - \frac{\partial I_3}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - | |||
\boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}}\right) + | |||
\left(I_3~\boldsymbol{\mathit{1}} - \frac{\partial I_4}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - | |||
\boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}}\right) = 0 ~. | |||
\end{align} | |||
</math> | |||
Then, invoking the arbitrariness of λ, we have | |||
:<math>\begin{align} | |||
I_0~\boldsymbol{\mathit{1}} - \frac{\partial I_1}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T\cdot\frac{\partial I_0}{\partial \boldsymbol{A}} & = 0 \\ | |||
I_1~\boldsymbol{\mathit{1}} - \frac{\partial I_2}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - I_2~\boldsymbol{\mathit{1}} - \frac{\partial I_3}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T\cdot\frac{\partial I_2}{\partial \boldsymbol{A}} & = 0 \\ | |||
I_3~\boldsymbol{\mathit{1}} - \frac{\partial I_4}{\partial \boldsymbol{A}}~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T\cdot\frac{\partial I_3}{\partial \boldsymbol{A}} & = 0 ~. | |||
\end{align}</math> | |||
This implies that | |||
:<math>\begin{align} | |||
\frac{\partial I_1}{\partial \boldsymbol{A}} &= \boldsymbol{\mathit{1}} \\ | |||
\frac{\partial I_2}{\partial \boldsymbol{A}} & = I_1~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T\\ | |||
\frac{\partial I_3}{\partial \boldsymbol{A}} & = I_2~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T~(I_1~\boldsymbol{\mathit{1}} - \boldsymbol{A}^T) = (\boldsymbol{A}^2 -I_1~\boldsymbol{A} + I_2~\boldsymbol{\mathit{1}})^T | |||
\end{align}</math> | |||
|} | |||
==Derivative of the second-order identity tensor== | |||
Let <math>\boldsymbol{\mathit{1}}</math> be the second order identity tensor. Then the derivative of this tensor with respect to a second order tensor <math>\boldsymbol{A}</math> is given by | |||
:<math> | |||
\frac{\partial \boldsymbol{\mathit{1}}}{\partial \boldsymbol{A}}:\boldsymbol{T} = \boldsymbol{\mathsf{0}}:\boldsymbol{T} = \boldsymbol{\mathit{0}} | |||
</math> | |||
This is because <math>\boldsymbol{\mathit{1}}</math> is independent of <math>\boldsymbol{A}</math>. | |||
==Derivative of a second-order tensor with respect to itself== | |||
Let <math>\boldsymbol{A}</math> be a second order tensor. Then | |||
:<math> | |||
\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}}:\boldsymbol{T} = \left[\frac{\partial }{\partial \alpha} (\boldsymbol{A} + \alpha~\boldsymbol{T})\right]_{\alpha = 0} = \boldsymbol{T} = \boldsymbol{\mathsf{I}}:\boldsymbol{T} | |||
</math> | |||
Therefore, | |||
:<math> | |||
\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}} | |||
</math> | |||
Here <math>\boldsymbol{\mathsf{I}}</math> is the fourth order identity tensor. In index | |||
notation with respect to an orthonormal basis | |||
:<math> | |||
\boldsymbol{\mathsf{I}} = \delta_{ik}~\delta_{jl}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l | |||
</math> | |||
This result implies that | |||
:<math> | |||
\frac{\partial \boldsymbol{A}^T}{\partial \boldsymbol{A}}:\boldsymbol{T} = \boldsymbol{\mathsf{I}}^T:\boldsymbol{T} = \boldsymbol{T}^T | |||
</math> | |||
where | |||
:<math> | |||
\boldsymbol{\mathsf{I}}^T = \delta_{jk}~\delta_{il}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l | |||
</math> | |||
Therefore, if the tensor <math>\boldsymbol{A}</math> is symmetric, then the derivative is also symmetric and | |||
we get | |||
:<math> | |||
\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}} = \boldsymbol{\mathsf{I}}^{(s)} | |||
= \frac{1}{2}~(\boldsymbol{\mathsf{I}} + \boldsymbol{\mathsf{I}}^T) | |||
</math> | |||
where the symmetric fourth order identity tensor is | |||
:<math> | |||
\boldsymbol{\mathsf{I}}^{(s)} = \frac{1}{2}~(\delta_{ik}~\delta_{jl} + \delta_{il}~\delta_{jk}) | |||
~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l | |||
</math> | |||
==Derivative of the inverse of a second-order tensor== | |||
Let <math>\boldsymbol{A}</math> and <math>\boldsymbol{T}</math> be two second order tensors, then | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}} \left(\boldsymbol{A}^{-1}\right) : \boldsymbol{T} = - \boldsymbol{A}^{-1}\cdot\boldsymbol{T}\cdot\boldsymbol{A}^{-1} | |||
</math> | |||
In index notation with respect to an orthonormal basis | |||
:<math> | |||
\frac{\partial A^{-1}_{ij}}{\partial A_{kl}}~T_{kl} = - A^{-1}_{ik}~T_{kl}~A^{-1}_{lj} \implies \frac{\partial A^{-1}_{ij}}{\partial A_{kl}} = - A^{-1}_{ik}~A^{-1}_{lj} | |||
</math> | |||
We also have | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}} \left(\boldsymbol{A}^{-T}\right) : \boldsymbol{T} = - \boldsymbol{A}^{-T}\cdot\boldsymbol{T}^{T}\cdot\boldsymbol{A}^{-T} | |||
</math> | |||
In index notation | |||
:<math> | |||
\frac{\partial A^{-1}_{ji}}{\partial A_{kl}}~T_{kl} = - A^{-1}_{jk}~T_{lk}~A^{-1}_{li} \implies \frac{\partial A^{-1}_{ji}}{\partial A_{kl}} = - A^{-1}_{li}~A^{-1}_{jk} | |||
</math> | |||
If the tensor <math>\boldsymbol{A}</math> is symmetric then | |||
:<math> | |||
\frac{\partial A^{-1}_{ij}}{\partial A_{kl}} = -\cfrac{1}{2}\left(A^{-1}_{ik}~A^{-1}_{jl} + A^{-1}_{il}~A^{-1}_{jk}\right) | |||
</math> | |||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" | |||
!Proof | |||
|- | |||
|Recall that | |||
:<math> | |||
\frac{\partial \boldsymbol{\mathit{1}}}{\partial \boldsymbol{A}}:\boldsymbol{T} = \boldsymbol{\mathit{0}} | |||
</math> | |||
Since <math>\boldsymbol{A}^{-1}\cdot\boldsymbol{A} = \boldsymbol{\mathit{1}}</math>, we can write | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}}(\boldsymbol{A}^{-1}\cdot\boldsymbol{A}):\boldsymbol{T} = \boldsymbol{\mathit{0}} | |||
</math> | |||
Using the product rule for second order tensors | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{S}}[\boldsymbol{F}_1(\boldsymbol{S})\cdot\boldsymbol{F}_2(\boldsymbol{S})]:\boldsymbol{T} = | |||
\left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)\cdot\boldsymbol{F}_2 + | |||
\boldsymbol{F}_1\cdot\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T}\right) | |||
</math> | |||
we get | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}}(\boldsymbol{A}^{-1}\cdot\boldsymbol{A}):\boldsymbol{T} = | |||
\left(\frac{\partial \boldsymbol{A}^{-1}}{\partial \boldsymbol{A}}:\boldsymbol{T}\right)\cdot\boldsymbol{A} + | |||
\boldsymbol{A}^{-1}\cdot\left(\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{A}}:\boldsymbol{T}\right) | |||
= \boldsymbol{\mathit{0}} | |||
</math> | |||
or, | |||
:<math> | |||
\left(\frac{\partial \boldsymbol{A}^{-1}}{\partial \boldsymbol{A}}:\boldsymbol{T}\right)\cdot\boldsymbol{A} = - | |||
\boldsymbol{A}^{-1}\cdot\boldsymbol{T} | |||
</math> | |||
Therefore, | |||
:<math> | |||
\frac{\partial }{\partial \boldsymbol{A}} \left(\boldsymbol{A}^{-1}\right) : \boldsymbol{T} = - \boldsymbol{A}^{-1}\cdot\boldsymbol{T}\cdot\boldsymbol{A}^{-1} | |||
</math> | |||
|} | |||
== Integration by parts == | |||
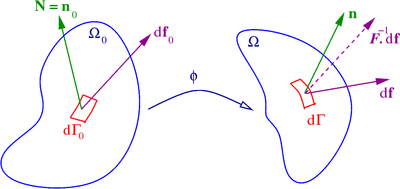
[[File:StressMeasures.png|thumb|400px|Domain <math>\Omega</math>, its boundary <math>\Gamma</math> and the outward unit normal <math>\mathbf{n}</math>]] | |||
Another important operation related to tensor derivatives in continuum mechanics is integration by parts. The formula for integration by parts can be written as | |||
:<math> | |||
\int_{\Omega} \boldsymbol{F}\otimes\boldsymbol{\nabla}\boldsymbol{G}\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\otimes(\boldsymbol{F}\otimes\boldsymbol{G})\,{\rm d}\Gamma - \int_{\Omega} \boldsymbol{G}\otimes\boldsymbol{\nabla}\boldsymbol{F}\,{\rm d}\Omega | |||
</math> | |||
where <math>\boldsymbol{F}</math> and <math>\boldsymbol{G}</math> are differentiable tensor fields of arbitrary order, <math>\mathbf{n}</math> is the unit outward normal to the domain over which the tensor fields are defined, <math>\otimes</math> represents a generalized tensor product operator, and <math>\boldsymbol{\nabla}</math> is a generalized gradient operator. When <math>\boldsymbol{F}</math> is equal to the identity tensor, we get the [[divergence theorem]] | |||
:<math> | |||
\int_{\Omega}\boldsymbol{\nabla}\boldsymbol{G}\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\otimes\boldsymbol{G}\,{\rm d}\Gamma \,. | |||
</math> | |||
We can express the formula for integration by parts in Cartesian index notation as | |||
:<math> | |||
\int_{\Omega} F_{ijk....}\,G_{lmn...,p}\,{\rm d}\Omega = \int_{\Gamma} n_p\,F_{ijk...}\,G_{lmn...}\,{\rm d}\Gamma - \int_{\Omega} G_{lmn...}\,F_{ijk...,p}\,{\rm d}\Omega \,. | |||
</math> | |||
For the special case where the tensor product operation is a contraction of one index and the gradient operation is a divergence, and both <math>\boldsymbol{F}</math> and <math>\boldsymbol{G}</math> are second order tensors, we have | |||
:<math> | |||
\int_{\Omega} \boldsymbol{F}\cdot(\boldsymbol{\nabla}\cdot\boldsymbol{G})\,{\rm d}\Omega = \int_{\Gamma} \mathbf{n}\cdot(\boldsymbol{G}\cdot\boldsymbol{F}^T)\,{\rm d}\Gamma - \int_{\Omega} (\boldsymbol{\nabla}\boldsymbol{F}):\boldsymbol{G}^T\,{\rm d}\Omega \,. | |||
</math> | |||
In index notation, | |||
:<math> | |||
\int_{\Omega} F_{ij}\,G_{pj,p}\,{\rm d}\Omega = \int_{\Gamma} n_p\,F_{ij}\,G_{pj}\,{\rm d}\Gamma - \int_{\Omega} G_{pj}\,F_{ij,p}\,{\rm d}\Omega \,. | |||
</math> | |||
== References == | |||
<references /> | |||
== See also == | |||
* [[Tensor derivative]] | |||
* [[Directional derivative]] | |||
* [[Curvilinear coordinates]] | |||
* [[Continuum mechanics]] | |||
[[Category:Solid mechanics]] | |||
[[Category:Mechanics]] | |||
Revision as of 18:57, 1 December 2013
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations.[1]
The directional derivative provides a systematic way of finding these derivatives.[2]
Derivatives with respect to vectors and second-order tensors
The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken.
Derivatives of scalar valued functions of vectors
Let f(v) be a real valued function of the vector v. Then the derivative of f(v) with respect to v (or at v) in the direction u is the vector defined as
for all vectors u.
Properties:
Derivatives of vector valued functions of vectors
Let f(v) be a vector valued function of the vector v. Then the derivative of f(v) with respect to v (or at v) in the direction u is the second order tensor defined as
for all vectors u.
- Properties:
Derivatives of scalar valued functions of second-order tensors
Let be a real valued function of the second order tensor . Then the derivative of with respect to (or at ) in the direction is the second order tensor defined as
for all second order tensors .
- Properties:
Derivatives of tensor valued functions of second-order tensors
Let be a second order tensor valued function of the second order tensor . Then the derivative of with respect to (or at ) in the direction is the fourth order tensor defined as
for all second order tensors .
- Properties:
Gradient of a tensor field
The gradient, , of a tensor field in the direction of an arbitrary constant vector c is defined as:
The gradient of a tensor field of order n is a tensor field of order n+1.
Cartesian coordinates
Template:Einstein summation convention
If are the basis vectors in a Cartesian coordinate system, with coordinates of points denoted by (), then the gradient of the tensor field is given by
Proof The vectors x and c can be written as and . Let y := x + αc. In that case the gradient is given by
Since the basis vectors do not vary in a Cartesian coordinate system we have the following relations for the gradients of a scalar field , a vector field v, and a second-order tensor field .
Curvilinear coordinates
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Template:Einstein summation convention
If are the contravariant basis vectors in a curvilinear coordinate system, with coordinates of points denoted by (), then the gradient of the tensor field is given by (see [3] for a proof.)
From this definition we have the following relations for the gradients of a scalar field , a vector field v, and a second-order tensor field .
where the Christoffel symbol is defined using
Cylindrical polar coordinates
In cylindrical coordinates, the gradient is given by
Divergence of a tensor field
The divergence of a tensor field is defined using the recursive relation
where c is an arbitrary constant vector and v is a vector field. If is a tensor field of order n > 1 then the divergence of the field is a tensor of order n−1.
Cartesian coordinates
Template:Einstein summation convention In a Cartesian coordinate system we have the following relations for a vector field v and a second-order tensor field .
Note that in the case of the second-order tensor field, we have[4]
Curvilinear coordinates
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. Template:Einstein summation convention In curvilinear coordinates, the divergences of a vector field v and a second-order tensor field are
Cylindrical polar coordinates
In cylindrical polar coordinates
Curl of a tensor field
The curl of an order-n > 1 tensor field is also defined using the recursive relation
where c is an arbitrary constant vector and v is a vector field.
Curl of a first-order tensor (vector) field
Consider a vector field v and an arbitrary constant vector c. In index notation, the cross product is given by
where is the permutation symbol. Then,
Therefore
Curl of a second-order tensor field
Hence, using the definition of the curl of a first-order tensor field,
Therefore, we have
Identities involving the curl of a tensor field
The most commonly used identity involving the curl of a tensor field, , is
This identity hold for tensor fields of all orders. For the important case of a second-order tensor, , this identity implies that
Derivative of the determinant of a second-order tensor
The derivative of the determinant of a second order tensor is given by
In an orthonormal basis, the components of can be written as a matrix A. In that case, the right hand side corresponds the cofactors of the matrix.
Derivatives of the invariants of a second-order tensor
The principal invariants of a second order tensor are
The derivatives of these three invariants with respect to are
Derivative of the second-order identity tensor
Let be the second order identity tensor. Then the derivative of this tensor with respect to a second order tensor is given by
This is because is independent of .
Derivative of a second-order tensor with respect to itself
Let be a second order tensor. Then
Therefore,
Here is the fourth order identity tensor. In index notation with respect to an orthonormal basis
This result implies that
where
Therefore, if the tensor is symmetric, then the derivative is also symmetric and we get
where the symmetric fourth order identity tensor is
Derivative of the inverse of a second-order tensor
Let and be two second order tensors, then
In index notation with respect to an orthonormal basis
We also have
In index notation
If the tensor is symmetric then
Proof Recall that Using the product rule for second order tensors
we get
or,
Therefore,
Integration by parts
Another important operation related to tensor derivatives in continuum mechanics is integration by parts. The formula for integration by parts can be written as
where and are differentiable tensor fields of arbitrary order, is the unit outward normal to the domain over which the tensor fields are defined, represents a generalized tensor product operator, and is a generalized gradient operator. When is equal to the identity tensor, we get the divergence theorem
We can express the formula for integration by parts in Cartesian index notation as
For the special case where the tensor product operation is a contraction of one index and the gradient operation is a divergence, and both and are second order tensors, we have
In index notation,
References
- ↑ J. C. Simo and T. J. R. Hughes, 1998, Computational Inelasticity, Springer
- ↑ J. E. Marsden and T. J. R. Hughes, 2000, Mathematical Foundations of Elasticity, Dover.
- ↑ Ogden, R. W., 2000, Nonlinear Elastic Deformations, Dover.
- ↑ http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/Part_III/Chapter_1_Vectors_Tensors/Vectors_Tensors_14_Tensor_Calculus.pdf
![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/308eadd1b18b96a60ef33e8df365bccc97f0faea)






![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8835d592f0ae810b9b57fa81f345a4850f1f1ce)









![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3916392ebeebca9ebddb31e76edb1c9f8c08b586)







![{\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2072ee23ca460f6f32851f397b5879a47033c3b)
















![{\begin{aligned}{\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot {\mathbf {c}}&=\left.{\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(x_{1}+\alpha c_{1},x_{2}+\alpha c_{2},x_{3}+\alpha c_{3})\right|_{{\alpha =0}}\equiv \left.{\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(y_{1},y_{2},y_{3})\right|_{{\alpha =0}}\\&=\left[{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{1}}}~{\cfrac {\partial y_{1}}{\partial \alpha }}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{2}}}~{\cfrac {\partial y_{2}}{\partial \alpha }}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{3}}}~{\cfrac {\partial y_{3}}{\partial \alpha }}\right]_{{\alpha =0}}=\left[{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{1}}}~c_{1}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{2}}}~c_{2}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial y_{3}}}~c_{3}\right]_{{\alpha =0}}\\&={\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{1}}}~c_{1}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{2}}}~c_{2}+{\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{3}}}~c_{3}\equiv {\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{i}}}~c_{i}={\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{i}}}~({\mathbf {e}}_{i}\cdot {\mathbf {c}})=\left[{\cfrac {\partial {{\boldsymbol {T}}}}{\partial x_{i}}}\otimes {\mathbf {e}}_{i}\right]\cdot {\mathbf {c}}\qquad \square \end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b848452c7189fb099eb1dadf20cd7c167dd4d2e)








![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\cfrac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\cfrac {1}{r}}~{\cfrac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\cfrac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} &={\cfrac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left({\cfrac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\cfrac {\partial v_{r}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\cfrac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left({\cfrac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\&\quad +{\cfrac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\cfrac {\partial v_{z}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}{\cfrac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\cfrac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\\&\quad +{\cfrac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\&\quad +{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}\\&\quad +{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}\\&\quad +{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\&\quad +{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\&\quad +{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\cfrac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757e0b753b3c6d9e2b58108a21b9da4fe14df3f4)




![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &={\cfrac {\partial v_{r}}{\partial r}}+{\cfrac {1}{r}}\left({\cfrac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\cfrac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\&+{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\cfrac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\&+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5562be336f10361b0049f7f3608f04208a4c03f2)











![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~[{\boldsymbol {A}}^{-1}]^{T}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb3bee9c5d16eb2b2f5d0827d4e39e8f83c65201)

![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {d}{d\alpha }}\det({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right|_{\alpha =0}\\&=\left.{\cfrac {d}{d\alpha }}\det \left[\alpha ~{\boldsymbol {A}}\left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}\\&=\left.{\cfrac {d}{d\alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\det \left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a280dfed26c159c4b698ac9db1c9e7b4ff9ce7c)


![{\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {d}{d\alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\left({\cfrac {1}{\alpha ^{3}}}+I_{1}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~{\cfrac {1}{\alpha ^{2}}}+I_{2}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~{\cfrac {1}{\alpha }}+I_{3}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})\right)\right]\right|_{{\alpha =0}}\\&=\left.\det({\boldsymbol {A}})~{\cfrac {d}{d\alpha }}\left[1+I_{1}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~\alpha +I_{2}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~\alpha ^{2}+I_{3}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~\alpha ^{3}\right]\right|_{{\alpha =0}}\\&=\left.\det({\boldsymbol {A}})~\left[I_{1}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})+2~I_{2}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~\alpha +3~I_{3}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~\alpha ^{2}\right]\right|_{{\alpha =0}}\\&=\det({\boldsymbol {A}})~I_{1}({\boldsymbol {A}}^{{-1}}\cdot {\boldsymbol {T}})~.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b8207ed9f2cc9582d921a734df86274e421fad)


![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\det({\boldsymbol {A}})~{\text{tr}}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}})=\det({\boldsymbol {A}})~[{\boldsymbol {A}}^{-1}]^{T}:{\boldsymbol {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80b13de7c7abc8d0c4e6853c644bfa9d82e6d0c3)
![{\frac {\partial f}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~[{\boldsymbol {A}}^{{-1}}]^{T}~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/080361970fc0603caedbc79b2b1c305f37897621)
![{\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A}})&={\frac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)
![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{T}\\{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~[{\boldsymbol {A}}^{-1}]^{T}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{T}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{T})=({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}})^{T}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/958082555bbf6e268f358d1286fab2eef6d5d5d0)
![{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~[{\boldsymbol {A}}^{-1}]^{T}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f59a269c296f625706d56b5bf8e45763228b86d)

![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}]^{T}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bf5247a085970a226c820d13945cd1a7220cd49)
![{\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {{\mathit {1}}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4ad226ea72ae236eaddfe419007ff6de53d55d)
![{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d73a983e1a52cffc7b3a033b31ea4e166f2ae2bb)
![{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{T}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd98450e2e00629178bedeee4200baed0a59616d)
![(\lambda ~{\boldsymbol {{\mathit {1}}}}+{\boldsymbol {A}}^{T})\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {{\mathit {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4716bd540dce8c574d01b9b956e33ac50244ae99)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a103ff061c93c7199e75f5a2e355b32fd81e0fee)


![{\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {{\mathit {1}}}}+{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{T}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {{\mathit {1}}}}~.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68503b4edd5ff8b08d4e88769764c4861dc553e3)





![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)















![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a25e5e0ee3f8a2f287da104d5f72d8342899b9)













