Smale conjecture: Difference between revisions
en>He to Hecuba added Category:Smooth manifolds using HotCat |
en>Michael Hardy The omission of the man's name is lunacy. |
||
| Line 1: | Line 1: | ||
In mathematics, the '''Coxeter complex''', named after [[H. S. M. Coxeter]], is a geometrical structure (a [[simplicial complex]]) associated to a [[Coxeter group]]. Coxeter complexes are the basic objects that allow the construction of [[building (mathematics)|buildings]]; they form the apartments of a building. | |||
==Construction== | |||
===The canonical linear representation=== | |||
The first ingredient in the construction of the Coxeter complex associated to a Coxeter group ''W'' is a certain [[representation (mathematics)|representation]] of ''W'', called the canonical representation of ''W''. | |||
Let <math>(W,S)</math> be a [[Coxeter group|Coxeter system]] associated to ''W'', with [[Coxeter group#Coxeter matrix|Coxeter matrix]] <math> M = (m(s,t))_{s,t \in S}</math>. The canonical representation is given by a vector space ''V'' with basis of formal symbols <math> (e_s)_{s \in S}</math>, which is equipped with the symmetric bilinear form <math> B(e_s,e_t) = - \cos \left ( \frac{\pi}{m(s,t)} \right )</math>. The action of ''W'' on this vector space ''V'' is then given by <math> s(v) = v - 2 \frac{B(e_s,v)}{B(e_s,e_s)}e_s</math>, as motivated by the expression for reflections in [[root system]]s. | |||
This representation has several foundational properties in the theory of Coxeter groups; for instance, the bilinear form ''B'' is positive definite if and only if ''W'' is finite. It is (always) a [[faithful representation]] of ''W''. | |||
===Chambers and the Tits cone=== | |||
One can think of this representation as expressing ''W'' as some sort of reflection group, with the caveat that ''B'' might not be positive definite. It becomes important then to distinguish the representation ''V'' with its dual ''V''<sup>*</sup>. The vectors <math>e_s</math> lie in ''V'', and have corresponding dual vectors <math>e_s^\vee</math> in ''V''<sup>*</sup>, given by: | |||
: <math> \langle e_s^\vee, v \rangle = 2 \frac{B(e_s,v)}{B(e_s,e_s)},</math> | |||
where the angled brackets indicate the natural pairing of a dual vector in ''V''<sup>*</sup> with a vector of ''V'', and ''B'' is the bilinear form as above. | |||
Now ''V'' acts on ''V''<sup>*</sup>, and the action satisfies the formula | |||
: <math> s(f) = f - \langle f, e_s \rangle e_s^\vee, \, </math> | |||
for <math> s \in S</math> and any ''f'' in ''V''<sup>*</sup>. This expresses ''s'' as a reflection in the hyperplane <math> H_s = \{ f \in V^*: \langle f, e_s \rangle = 0 \}</math>. One has the fundamental chamber <math> \mathcal{C} = \{ f \in V^* : \langle f, e_s \rangle > 0 \ \forall s \in S \}</math>, this has faces the so-called walls, <math>H_s</math>. The other chambers can be obtained from <math>\mathcal{C}</math> by translation: they are the <math> w\mathcal{C} </math> for <math> w \in W</math>. | |||
Given a fundamental chamber <math> \mathcal{C}</math>, the '''Tits cone''' is defined to be <math> X = \bigcup_{w \in W} w \overline{\mathcal{C}}</math>. This need not be the whole of ''V''<sup>*</sup>. Of major importance is the fact that the Tits cone ''X'' is convex. The action of ''W'' on the Tits cone ''X'' has [[fundamental domain]] the fundamental chamber <math> \mathcal{C}</math>. | |||
===The Coxeter complex=== | |||
Once one has defined the Tits cone ''X'', the Coxeter complex <math>\Sigma(W,S)</math> of ''W'' with respect to ''S'' can be defined as the quotient of ''X'', with the origin removed, under multiplication by the positive reals, <math> \Sigma(W,S) = (X \setminus \{ 0 \}) / \mathbb{R}_{>0}^\times</math>. | |||
==Examples== | |||
===Finite dihedral groups=== | |||
The dihedral groups <math>D_n</math> (of order 2''n'') are Coxeter groups, of corresponding type <math> \mathrm{I}_2(n)</math>. These have the presentation <math> \left \langle s, t \, \left | \, s^2, t^2, (st)^n \right \rangle \right . </math>. | |||
The canonical linear representation of <math> \mathrm{I}_2(n)</math> is the usual reflection representation of the dihedral group, as acting on a ''n''-gon in the plane (so <math> V = \mathbb{R}^2</math> in this case). For instance, in the case ''n'' = 3, we get the Coxeter group of type <math> \mathrm{I}_2(3) = \mathrm{A}_2</math>, acting on an equilateral triangle in the plane. Each reflection ''s'' has an associated hyperplane ''H''<sub>''s''</sub> in the dual vector space (which can be canonically identified with the vector space itself using the bilinear form ''B'', which is an inner product in this case as remarked above), these are the walls. They cut out chambers, as seen below: | |||
[[File:Spherical dihedral complex.svg | 300px]] | |||
The Coxeter complex is then the corresponding 2''n''-gon, as in the previous image. This is a simplicial complex of dimension 1, and it can be colored by cotype. | |||
===The infinite dihedral group=== | |||
Another motivating example is the [[infinite dihedral group]] <math> D_{\infty} </math>. This can be seen as the group of symmetries of the real line that preserves the set of points with integer coordinates; it is generated by the reflections in <math> x= 0 </math> and <math> x = 1 </math>. This group has the Coxeter presentation <math> \left \langle s, t \, \left | \, s^2, t^2 \right \rangle \right . </math>. | |||
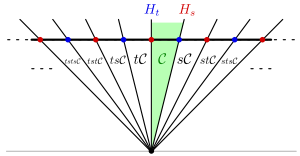
In this case, it is no longer possible to identify ''V'' with the dual space ''V''<sup>*</sup>, as ''B'' is not positive definite. It is then better to work solely with ''V''<sup>*</sup>, which is where the hyperplanes are defined. This then gives the following picture: | |||
[[Image:Affine dihedral complex.svg|300px]] | |||
In this case, the Tits cone is not the whole plane, but only the upper half plane. Quotienting out by the positive reals then yields another copy of the real line, with marked points at the integers. This is the Coxeter complex of the infinite dihedral group. | |||
==Alternative construction of the Coxeter complex== | |||
Another description of the Coxeter complex uses standard cosets of the Coxeter group ''W''. A standard coset is a coset of the form <math> w W_J </math>, where <math> W_J = \langle J \rangle</math> for some subset ''J'' of ''S''. For instance, <math> W_S = W </math> and <math> W_\emptyset = \{1\}</math>. | |||
The Coxeter complex <math> \Sigma(W,S) </math> is then the [[poset]] of standard cosets, ordered by reverse inclusion. This has a canonical structure of a simplicial complex, as do all posets that satisfy: | |||
*Any two elements have a greatest lower bound. | |||
*The poset of elements less than or equal to any given element is isomorphic to the poset of subsets of <math> \{1, 2, \ldots, n \}</math> for some integer ''n''. | |||
==Properties== | |||
The Coxeter complex associated to <math>(W,S)</math> has dimension <math>|S|-1</math>. It is homeomorphic to a <math>(|S|-1)</math>-sphere if ''W'' is finite and is [[contractible space|contractible]] if ''W'' is infinite. | |||
==See also== | |||
*[[Building (mathematics)|Buildings]] | |||
*[[Weyl group]] | |||
*[[Root system]] | |||
==References== | |||
* Peter Abramenko and Kenneth S. Brown, ''Buildings, Theory and Applications''. Springer, 2008. | |||
[[Category:Group theory]] | |||
[[Category:Coxeter groups| ]] | |||
[[Category:Algebraic combinatorics]] | |||
[[Category:Geometric group theory]] | |||
[[Category:Mathematical structures]] | |||
Revision as of 09:00, 24 June 2013
In mathematics, the Coxeter complex, named after H. S. M. Coxeter, is a geometrical structure (a simplicial complex) associated to a Coxeter group. Coxeter complexes are the basic objects that allow the construction of buildings; they form the apartments of a building.
Construction
The canonical linear representation
The first ingredient in the construction of the Coxeter complex associated to a Coxeter group W is a certain representation of W, called the canonical representation of W.
Let be a Coxeter system associated to W, with Coxeter matrix . The canonical representation is given by a vector space V with basis of formal symbols , which is equipped with the symmetric bilinear form . The action of W on this vector space V is then given by , as motivated by the expression for reflections in root systems.
This representation has several foundational properties in the theory of Coxeter groups; for instance, the bilinear form B is positive definite if and only if W is finite. It is (always) a faithful representation of W.
Chambers and the Tits cone
One can think of this representation as expressing W as some sort of reflection group, with the caveat that B might not be positive definite. It becomes important then to distinguish the representation V with its dual V*. The vectors lie in V, and have corresponding dual vectors in V*, given by:
where the angled brackets indicate the natural pairing of a dual vector in V* with a vector of V, and B is the bilinear form as above.
Now V acts on V*, and the action satisfies the formula
for and any f in V*. This expresses s as a reflection in the hyperplane . One has the fundamental chamber , this has faces the so-called walls, . The other chambers can be obtained from by translation: they are the for .
Given a fundamental chamber , the Tits cone is defined to be . This need not be the whole of V*. Of major importance is the fact that the Tits cone X is convex. The action of W on the Tits cone X has fundamental domain the fundamental chamber .
The Coxeter complex
Once one has defined the Tits cone X, the Coxeter complex of W with respect to S can be defined as the quotient of X, with the origin removed, under multiplication by the positive reals, .
Examples
Finite dihedral groups
The dihedral groups (of order 2n) are Coxeter groups, of corresponding type . These have the presentation .
The canonical linear representation of is the usual reflection representation of the dihedral group, as acting on a n-gon in the plane (so in this case). For instance, in the case n = 3, we get the Coxeter group of type , acting on an equilateral triangle in the plane. Each reflection s has an associated hyperplane Hs in the dual vector space (which can be canonically identified with the vector space itself using the bilinear form B, which is an inner product in this case as remarked above), these are the walls. They cut out chambers, as seen below:
The Coxeter complex is then the corresponding 2n-gon, as in the previous image. This is a simplicial complex of dimension 1, and it can be colored by cotype.
The infinite dihedral group
Another motivating example is the infinite dihedral group . This can be seen as the group of symmetries of the real line that preserves the set of points with integer coordinates; it is generated by the reflections in and . This group has the Coxeter presentation .
In this case, it is no longer possible to identify V with the dual space V*, as B is not positive definite. It is then better to work solely with V*, which is where the hyperplanes are defined. This then gives the following picture:
In this case, the Tits cone is not the whole plane, but only the upper half plane. Quotienting out by the positive reals then yields another copy of the real line, with marked points at the integers. This is the Coxeter complex of the infinite dihedral group.
Alternative construction of the Coxeter complex
Another description of the Coxeter complex uses standard cosets of the Coxeter group W. A standard coset is a coset of the form , where for some subset J of S. For instance, and .
The Coxeter complex is then the poset of standard cosets, ordered by reverse inclusion. This has a canonical structure of a simplicial complex, as do all posets that satisfy:
- Any two elements have a greatest lower bound.
- The poset of elements less than or equal to any given element is isomorphic to the poset of subsets of for some integer n.
Properties
The Coxeter complex associated to has dimension . It is homeomorphic to a -sphere if W is finite and is contractible if W is infinite.
See also
References
- Peter Abramenko and Kenneth S. Brown, Buildings, Theory and Applications. Springer, 2008.