Product of rings: Difference between revisions
en>Helpful Pixie Bot m ISBNs (Build KH) |
en>Quondum Minor formatting (mainly {{nowrap}}) |
||
| Line 1: | Line 1: | ||
[[Image:Wave group.gif|frame|[[Dispersion (water waves)|Frequency dispersion]] in groups of [[gravity waves]] on the surface of deep water. The red dot moves with the phase velocity, and the green dots propagate with the [[group velocity]]. In this deep-water case, the phase velocity is twice the group velocity. The red dot overtakes two green dots when moving from the left to the right of the figure.<br>New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.<br>For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.]] | |||
[[Image:Wave opposite-group-phase-velocity.gif|thumb|frame|right|This shows a wave with the group velocity and phase velocity going in different directions. The group velocity is positive, while the phase velocity is negative.<ref name=nemirovsky2012negative>{{cite journal|last=Nemirovsky|first=Jonathan|coauthors=Rechtsman, Mikael C and Segev, Mordechai|title=Negative radiation pressure and negative effective refractive index via dielectric birefringence|journal=Optics Express|date=9 April 2012|volume=20|issue=8|pages=8907–8914|doi=10.1364/OE.20.008907|url=http://physics.technion.ac.il/~msegev/publications/NRP_Opt_Exp.pdf}}</ref>]] | |||
The '''phase velocity''' of a [[wave]] is the rate at which the [[phase (waves)|phase]] of the wave [[Wave propagation|propagates in space]]. This is the [[velocity]] at which the phase of any one [[frequency]] component of the wave travels. For such a component, any given phase of the wave (for example, the [[crest (physics)|crest]]) will appear to travel at the phase velocity. The phase velocity is given in terms of the [[wavelength]] ''λ'' (lambda) and [[Wave period|period]] ''T'' as | |||
:<math>v_\mathrm{p} = \frac{\lambda}{T}.</math> | |||
Or, equivalently, in terms of the wave's [[angular frequency]] ''ω'', which specifies angular change per unit of time, and [[wavenumber]] (or angular wave number) ''k'', which represents the proportionality between the angular frequency ω and the linear speed (speed of propagation) ν<sub>p</sub>: | |||
:<math>v_\mathrm{p} = \frac{\omega}{k}.</math> | |||
To understand where this equation comes from, imagine a basic [[sine wave]], ''A'' cos (''kx''−''ωt''). Given time ''t'', the source produces ''ωt/2π = ft'' oscillations. At the same time, the initial wave front propagates away from the source through the space to the distance ''x'' to fit the same amount of oscillations, ''kx'' = ''ωt''. So that the propagation velocity ''v'' is ''v'' = ''x''/''t'' = ''ω''/''k''. The wave propagates faster when higher frequency oscillations are distributed less densely in space.<ref name="mathpages1">{{cite web|url=http://www.mathpages.com/home/kmath210/kmath210.htm |title=Phase, Group, and Signal Velocity |publisher=Mathpages.com |date= |accessdate=2011-07-24}}</ref> Formally, ''Φ'' = ''kx''−''ωt'' is the phase. Since ''ω'' = −d''Φ''/d''t'' and ''k'' = +d''Φ''/d''x'', the wave velocity is ''v'' = d''x''/d''t'' = ''ω''/''k''. | |||
== Relation to group velocity, refractive index and transmission speed == | |||
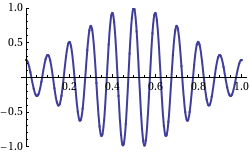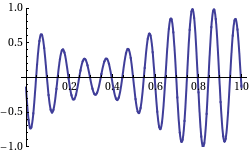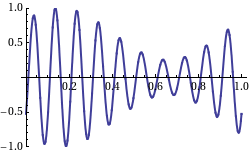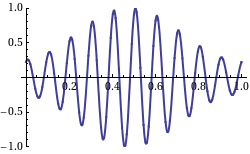
Since a pure sine wave cannot convey any information, some change in amplitude or frequency, known as [[modulation]], is required. By combining two sines with slightly different frequencies and wavelengths, | |||
:<math>\cos[(k-\Delta k)x-(\omega-\Delta\omega)t]\; +\; \cos[(k+\Delta k)x-(\omega+\Delta\omega)t] = 2\; \cos(\Delta kx-\Delta\omega t)\; \cos(kx-\omega t),</math> | |||
the amplitude becomes a sinusoid with phase speed of ''v''<sub>g</sub> = Δ''ω''/Δ''k''. It is this modulation that represents the signal content. Since each amplitude ''envelope'' contains a group of internal waves, this speed is usually called the [[group velocity]].<ref name="mathpages1"/> | |||
In reality, the ''v''<sub>p</sub> = ''ω''/''k'' and ''v''<sub>g</sub> = d''ω''/d''k'' ratios are determined by the media. The relation between phase speed, ''v''<sub>p</sub>, and speed of light, ''c'', is known as [[refractive index]], ''n'' = ''c''/''v''<sub>p</sub> = ''ck''/''ω''. Taking the derivative of ''ω'' = ''ck''/''n'', we get the group speed, | |||
:<math>\frac{\text{d}\omega}{\text{d}k} = \frac{c}{n} - \frac{ck}{n^2}\cdot\frac{\text{d}n}{\text{d}k}.</math> | |||
Noting that ''c''/''n'' = ''v''<sub>p</sub>, this shows that group speed is equal to phase speed only when the refractive index is a constant: d''n''/d''k'' = 0.<ref name="mathpages1"/> Otherwise, when the phase velocity varies with frequency, velocities differ and the medium is called [[dispersion (optics)|dispersive]] and the function, <math>\omega(k)</math>, from which the group velocity is derived is known as a [[dispersion relation]]. | |||
The group velocity of [[electromagnetic radiation]] may – under certain circumstances (for example [[anomalous dispersion]]) – exceed the [[speed of light]] in a vacuum, but this does not indicate any [[superluminal]] information or energy transfer. It was theoretically described by physicists such as [[Arnold Sommerfeld]] and [[Léon Brillouin]]. See [[dispersion (optics)|dispersion]] for a full discussion of wave velocities. | |||
== See also == | |||
*[[Cherenkov radiation]] | |||
*[[Dispersion (optics)]] | |||
*[[Group velocity]] | |||
*[[Propagation delay]] | |||
*[[Shear wave splitting]] | |||
*[[Wave propagation]] | |||
*[[Wave propagation speed]] | |||
*[[Planck constant]] | |||
*[[Matter wave#Phase velocity]] | |||
==References== | |||
===Footnotes=== | |||
{{reflist}} | |||
===Other=== | |||
{{refbegin}} | |||
*{{citation | author-link=Léon Brillouin | last=Brillouin |first=Léon |title=Wave Propagation And Group Velocity |publisher=Academic Press Inc. |location=New York and London |year=1960 |isbn=0-12-134968-3 }} | |||
*{{citation |last=Main |first=Iain G. |year=1988 |title=Vibrations and Waves in Physics |edition=2nd |location=New York |publisher=Cambridge University Press |isbn=0-521-27846-5 |pages=214–216 }} | |||
*{{citation |last1=Tipler |first1=Paul A. |first2=Ralph A. |last2=Llewellyn |year=2003 |title=Modern Physics |edition=4th |location=New York |publisher=W. H. Freeman and Company |isbn=0-7167-4345-0 |pages=222–223 }} | |||
{{refend}} | |||
== External links == | |||
* [http://gregegan.customer.netspace.net.au/APPLETS/20/20.html Subluminal] – A Java applet | |||
* [http://www.falstad.com/dispersion/ Simulation] – A Java applet by Paul Falstad | |||
* [http://publicliterature.org/tools/group_and_phase_velocity/ Group and Phase Velocity] – Java applet showing the difference between group and phase velocity. | |||
{{Velocities of Waves}} | |||
<!-- interwiki kept as they link to sections --> | |||
[[Category:Wave mechanics]] | |||
[[fr:Vitesse d'une onde#Vitesse de phase]] | |||
[[nl:Voortplantingssnelheid#Fase- en groepssnelheid]] | |||
Latest revision as of 04:06, 4 August 2013

New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.
For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and period T as
Or, equivalently, in terms of the wave's angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represents the proportionality between the angular frequency ω and the linear speed (speed of propagation) νp:
To understand where this equation comes from, imagine a basic sine wave, A cos (kx−ωt). Given time t, the source produces ωt/2π = ft oscillations. At the same time, the initial wave front propagates away from the source through the space to the distance x to fit the same amount of oscillations, kx = ωt. So that the propagation velocity v is v = x/t = ω/k. The wave propagates faster when higher frequency oscillations are distributed less densely in space.[2] Formally, Φ = kx−ωt is the phase. Since ω = −dΦ/dt and k = +dΦ/dx, the wave velocity is v = dx/dt = ω/k.
Relation to group velocity, refractive index and transmission speed
Since a pure sine wave cannot convey any information, some change in amplitude or frequency, known as modulation, is required. By combining two sines with slightly different frequencies and wavelengths,
the amplitude becomes a sinusoid with phase speed of vg = Δω/Δk. It is this modulation that represents the signal content. Since each amplitude envelope contains a group of internal waves, this speed is usually called the group velocity.[2] In reality, the vp = ω/k and vg = dω/dk ratios are determined by the media. The relation between phase speed, vp, and speed of light, c, is known as refractive index, n = c/vp = ck/ω. Taking the derivative of ω = ck/n, we get the group speed,
Noting that c/n = vp, this shows that group speed is equal to phase speed only when the refractive index is a constant: dn/dk = 0.[2] Otherwise, when the phase velocity varies with frequency, velocities differ and the medium is called dispersive and the function, , from which the group velocity is derived is known as a dispersion relation. The group velocity of electromagnetic radiation may – under certain circumstances (for example anomalous dispersion) – exceed the speed of light in a vacuum, but this does not indicate any superluminal information or energy transfer. It was theoretically described by physicists such as Arnold Sommerfeld and Léon Brillouin. See dispersion for a full discussion of wave velocities.
See also
- Cherenkov radiation
- Dispersion (optics)
- Group velocity
- Propagation delay
- Shear wave splitting
- Wave propagation
- Wave propagation speed
- Planck constant
- Matter wave#Phase velocity
References
Footnotes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
Other
- Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010 - Many property agents need to declare for the PIC grant in Singapore. However, not all of them know find out how to do the correct process for getting this PIC scheme from the IRAS. There are a number of steps that you need to do before your software can be approved.
Naturally, you will have to pay a safety deposit and that is usually one month rent for annually of the settlement. That is the place your good religion deposit will likely be taken into account and will kind part or all of your security deposit. Anticipate to have a proportionate amount deducted out of your deposit if something is discovered to be damaged if you move out. It's best to you'll want to test the inventory drawn up by the owner, which can detail all objects in the property and their condition. If you happen to fail to notice any harm not already mentioned within the inventory before transferring in, you danger having to pay for it yourself.
In case you are in search of an actual estate or Singapore property agent on-line, you simply should belief your intuition. It's because you do not know which agent is nice and which agent will not be. Carry out research on several brokers by looking out the internet. As soon as if you end up positive that a selected agent is dependable and reliable, you can choose to utilize his partnerise in finding you a home in Singapore. Most of the time, a property agent is taken into account to be good if he or she locations the contact data on his website. This may mean that the agent does not mind you calling them and asking them any questions relating to new properties in singapore in Singapore. After chatting with them you too can see them in their office after taking an appointment.
Have handed an trade examination i.e Widespread Examination for House Brokers (CEHA) or Actual Property Agency (REA) examination, or equal; Exclusive brokers are extra keen to share listing information thus making certain the widest doable coverage inside the real estate community via Multiple Listings and Networking. Accepting a severe provide is simpler since your agent is totally conscious of all advertising activity related with your property. This reduces your having to check with a number of agents for some other offers. Price control is easily achieved. Paint work in good restore-discuss with your Property Marketing consultant if main works are still to be done. Softening in residential property prices proceed, led by 2.8 per cent decline within the index for Remainder of Central Region
Once you place down the one per cent choice price to carry down a non-public property, it's important to accept its situation as it is whenever you move in – faulty air-con, choked rest room and all. Get round this by asking your agent to incorporate a ultimate inspection clause within the possibility-to-buy letter. HDB flat patrons routinely take pleasure in this security net. "There's a ultimate inspection of the property two days before the completion of all HDB transactions. If the air-con is defective, you can request the seller to repair it," says Kelvin.
15.6.1 As the agent is an intermediary, generally, as soon as the principal and third party are introduced right into a contractual relationship, the agent drops out of the image, subject to any problems with remuneration or indemnification that he could have against the principal, and extra exceptionally, against the third occasion. Generally, agents are entitled to be indemnified for all liabilities reasonably incurred within the execution of the brokers´ authority.
To achieve the very best outcomes, you must be always updated on market situations, including past transaction information and reliable projections. You could review and examine comparable homes that are currently available in the market, especially these which have been sold or not bought up to now six months. You'll be able to see a pattern of such report by clicking here It's essential to defend yourself in opposition to unscrupulous patrons. They are often very skilled in using highly unethical and manipulative techniques to try and lure you into a lure. That you must also protect your self, your loved ones, and personal belongings as you'll be serving many strangers in your home. Sign a listing itemizing of all of the objects provided by the proprietor, together with their situation. HSR Prime Recruiter 2010
External links
- Subluminal – A Java applet
- Simulation – A Java applet by Paul Falstad
- Group and Phase Velocity – Java applet showing the difference between group and phase velocity.
fr:Vitesse d'une onde#Vitesse de phase nl:Voortplantingssnelheid#Fase- en groepssnelheid
- ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 2.0 2.1 2.2 Template:Cite web


![{\displaystyle \cos[(k-\Delta k)x-(\omega -\Delta \omega )t]\;+\;\cos[(k+\Delta k)x-(\omega +\Delta \omega )t]=2\;\cos(\Delta kx-\Delta \omega t)\;\cos(kx-\omega t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e67ea4a20e17a492a1f91226b4a17aa3ec5c548)

