Lenstra–Lenstra–Lovász lattice basis reduction algorithm: Difference between revisions
en>Roberticus m Reverted 1 edit by 69.123.75.119 identified as test/vandalism using STiki |
|||
| Line 1: | Line 1: | ||
I | {{cleanup|reason=The article is fundamentally wrong and packed with errors based on the authors' poor understanding of the subject|date=February 2013}} | ||
{{expert-subject|date=November 2012|reason=Lots of anon editors have changed values in formulae - may now be incorrect|Mathematics}} | |||
:''This article is about the geometrical property of an area, termed the second moment of area. For the moment of inertia dealing with the rotation of an object with mass, see [[mass moment of inertia]].'' | |||
:''For a list, see [[list of area moments of inertia]].'' | |||
The '''second moment of area''', also known as '''moment of inertia of plane area''', '''area moment of inertia''', '''polar moment of inertia''' or '''second area moment''', is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an <math>I</math> for an axis that lies in the plane or with a <math>J</math> for an axis perpendicular to the plane. Its [[physical unit|unit]] of dimension is length to fourth power, [[Unit_of_length|L]]<sup>4</sup>. | |||
In the field of [[structural engineering]], the second moment of area of the cross-section of a [[beam (structure)|beam]] is an important property used in the calculation of [[deflection (engineering)|deflection]]. | |||
==Definition== | |||
[[File:Polar Moment of Inertia.svg|frame|right|A schematic showing how the '''polar moment of inertia''' is calculated for an arbitrary shape with respect to the ''z'' axis. ''ρ'' is the radial distance to the element ''dA'', with projections ''x'' and ''y'' on the axes.]] | |||
The second moment of area for an arbitrary shape with respect to an arbitrary axis <math>BB</math> is defined as | |||
: <math>J_{BB} = \int_A {\rho}^2 \, \mathrm dA</math> | |||
: <math>\mathrm dA</math> = Differential area of the arbitrary shape | |||
: <math>\rho</math> = Distance from the axis BB to dA | |||
For example, when the desired reference axis is the x-axis the second moment of area, <math>I_{xx}</math> (often denoted as <math>I_x</math>) can be computed in [[Cartesian coordinates]] as | |||
: <math>I_{x} = \iint_A y^2\, \mathrm dx\, \mathrm dy</math> | |||
== Parallel axis theorem == | |||
{{Main|Parallel axis theorem}} | |||
It is often easier to derive the second moment of area with respect to its centroidal axis, <math>x'</math>. However, it may be necessary to calculate the second moment of area with respect to a different, parallel axis, say the <math>x</math> axis. The parallel axis theorem states | |||
: <math>I_x = I_{x'} + A d_y^2</math> | |||
where | |||
: <math>A</math> = Area of the shape | |||
: <math>d_y</math> = Perpendicular distance between the <math>x'</math> and <math>x</math> axes | |||
A similar statement can be made about the <math>y</math> axis and the parallel centroidal <math>y'</math> axis. Or, in general, any centroidal <math>B'</math> axis and a parallel <math>B</math> axis. | |||
== Perpendicular axis theorem == | |||
{{Main|Perpendicular axis theorem}} | |||
For the simplicity of calculation, it is often desired to define the polar moment of inertia (with respect to a perpendicular axis) in terms of two area moments of inertia (both with respect to in-plane axes). The simplest case relates <math>J_z</math> to <math>I_x</math> and <math>I_y</math>. | |||
: <math>J_z = \int_A \rho^2\,\mathrm dA = \int_A (x^2 + y^2)\,\mathrm dA = \int_A x^2\,\mathrm dA + \int_A y^2\,\mathrm dA = I_x + I_y</math> | |||
This relationship relies on the [[Pythagorean theorem]] which relates <math>x</math> and <math>y</math> to <math>\rho</math> and on the [[linearity of integration]]. | |||
== Composite shapes == | |||
For more complex areas, it is often easier to divide the area into a series of "simpler" shapes. The second moment of area for the entire shape is the sum of the second moment of areas of all of its parts about a common axis. This can include shapes that are "missing" (i.e. holes, hollow shapes, etc.), in which case the second moment of area of the "missing" areas are subtracted, rather than added. In other words, the second moment of area of "missing" parts are considered negative for the method of composite shapes. | |||
==Examples== | |||
See [[list of area moments of inertia]] for other cross-sections. | |||
===Rectangle with centroid at the origin=== | |||
Consider a rectangle with base <math>b</math> and height <math>h</math> whose [[centroid]] is located at the origin. <math>I_x</math> represents the second moment of area with respect to the x-axis; <math>I_y</math> represents the second moment of area with respect to the y-axis; <math>J_z</math> represents the polar moment of inertia with respect to the z-axis. | |||
<span style="padding-right: 24px">[[Image:block centroid axes.svg|right|280px]]</span> | |||
: <math>I_{x} = \int_A y^2\,\mathrm dA = \int^{b/2}_{-b/2} \int^{h/2}_{-h/2} y^2 \,\mathrm dy \,\mathrm dx = \int^{b/2}_{-b/2} \frac{1}{3}\frac{h^3}{4}\,\mathrm dx = \frac{b h^3}{12}</math> | |||
: <math>I_{y} = \int_A x^2\,\mathrm dA = \int^{b/2}_{-b/2} \int^{h/2}_{-h/2} x^2 \,\mathrm dy \,\mathrm dx = \int^{b/2}_{-b/2} h x^2\,\mathrm dx = \frac{b^3 h}{12}</math> | |||
: <math>J_{z} = I_x + I_y = \frac{b h^3}{12} + \frac{h b^3}{12} = \frac{b h}{12}(b^2 + h^2)</math> (see [[second moment of area#Perpendicular axis theorem|Perpendicular axis theorem]]) | |||
===Annulus centered at origin=== | |||
<span style="padding-left: 24px">[[Image:Second_Moment_of_Area,_Annulus.svg|right|175px]]</span> | |||
Consider an [[annulus (mathematics)|annulus]] whose center is at the origin, outside radius is <math>r_o</math>, and inside radius is <math>r_i</math>. Because of the symmetry of the annulus, the centroid also lies at the origin. We can determine the polar moment of inertia, <math>J_z</math>, about the <math>z</math> axis by the method of composite shapes. This polar moment of inertia is equivalent to the polar moment of inertia of a circle with radius <math>r_o</math> minus the polar moment of inertia of a circle with radius <math>r_i</math>, both centered at the origin. First, let us derive the polar moment of inertia of a circle with radius <math>r</math> with respect to the origin. In this case, it is easier to directly calculate <math>J_z</math> as we already have <math>r^2</math>, which has both an <math>x</math> and <math>y</math> component. Instead of calculating <math>I_x</math> and <math>I_y</math> as done in the previous section, we shall calculate <math>J_z</math> directly using [[Polar Coordinates]]. | |||
<math>J_{z, circle} = \iint r^2\,dA = \int_0^{2\pi}\int_0^r r^2\left(r\,dr\,d\theta\right) = \int_0^{2\pi}\int_0^r r^3\,dr\,d\theta = \int_0^{2\pi} \frac{r^4}{4}\,d\theta = \frac{\pi}{2}r^4</math> | |||
Now, the polar moment of inertia about the <math>z</math> axis for an annulus is simply, as stated above, the difference of the second moments of area of a circle with radius <math>r_o</math> and a circle with radius <math>r_i</math>. | |||
<math>J_{z} = J_{z, r_o} - J_{z, r_i} = \frac{\pi}{2}r_o^4 - \frac{\pi}{2}r_i^4 = \frac{\pi}{2}({r_o} ^4 - {r_i} ^4)</math> | |||
Alternatively, we could change the limits on the <math>dr</math> integral the first time around to reflect the fact that there is a hole. This would be done like this. | |||
<math>J_{z} = \iint r^2\,dA = \int_0^{2\pi}\int_{r_i}^{r_o} r^2\left(r\,dr\,d\theta\right) = \int_0^{2\pi}\int_{r_i}^{r_o} r^3\,dr\,d\theta = \int_0^{2\pi}\left[\frac{r_o^4}{4} - \frac{r_i^4}{4}\right]\,d\theta = \frac{\pi}{2}\left(r_o^4 - r_i^4\right)</math> | |||
===Any polygon=== | |||
The second moment of area for any [[simple polygon]] on the XY-plane can be computed in general by summing contributions from each segment of the polygon (method of composite shapes)(order of iteration along the poligon vertex gives sign to the value calculated). | |||
[[File:Polygon vertex labels.svg|thumb|320px|right|Nomenclature of a 2D polygon.]] | |||
:<math>I_{x} = \frac{1}{12} \sum_{i = 1}^{n} ( x_{i+1} - x_i ) ( y_{i+1} + y_i ) ( y_{i+1}^2 + y_i^2 )\,</math> | |||
:<math>I_{y} = \frac{1}{12} \sum_{i = 1}^{n} ( y_{i+1} - y_i ) ( x_{i+1} + x_i ) ( x_{i+1}^2 + x_i^2 )\,</math> | |||
:<math>I_{xy} = \frac{1}{24} \sum_{i = 1}^{n} ( x_i - x_{i+1} ) ( 3 x_{i+1} y_{i+1}^2 + x_i y_{i+1}^2 + 2 x_{i+1} y_i y_{i+1} + 2 x_i y_i y_{i+1} + x_{i+1} y_i^2 + 3 x_i^2 y_i^2 )\,</math> | |||
where : <math> x_i , y_i</math> are the coordinates of any polygon vertex<ref>[http://simetriamecanica.es/5.html Mechanical Symmetry] by Joaquin Obregon - December 2012 - ISBN 978 1 4772 3372 6</ref> - www.mecsym.org | |||
==See also== | |||
* [[List of area moments of inertia]] | |||
* [[List of moments of inertia]] | |||
* [[Moment of inertia]] | |||
* [[Parallel axis theorem]] | |||
* [[Perpendicular axis theorem]] | |||
* [[Radius of gyration]] | |||
==References== | |||
*{{cite book | |||
| last = Pilkey | |||
| first = Walter D. | |||
| title = Analysis and Design of Elastic Beams | |||
| year = 2002 | |||
| publisher = John Wiley & Sons, Inc. | |||
| isbn = 0-471-38152-7 | |||
}} | |||
*{{cite book | |||
| last = Hibbeler | |||
| first = R. C. | |||
| title = Statics and Mechanics of Materials | |||
| edition = Second | |||
| year = 2004 | |||
| publisher = Pearson Prentice Hall | |||
| isbn = 0-13-028127-1 | |||
}} | |||
<references/> | |||
==External links== | |||
* [http://civilengineer.webinfolist.com/str/micalc.htm Calculator for Second Moment of Area] | |||
[[Category:Geometry]] | |||
[[Category:Structural analysis]] | |||
[[Category:Physical quantities]] | |||
Revision as of 23:07, 17 October 2013
Template:Cleanup Template:Expert-subject
- This article is about the geometrical property of an area, termed the second moment of area. For the moment of inertia dealing with the rotation of an object with mass, see mass moment of inertia.
- For a list, see list of area moments of inertia.
The second moment of area, also known as moment of inertia of plane area, area moment of inertia, polar moment of inertia or second area moment, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an for an axis that lies in the plane or with a for an axis perpendicular to the plane. Its unit of dimension is length to fourth power, L4.
In the field of structural engineering, the second moment of area of the cross-section of a beam is an important property used in the calculation of deflection.
Definition
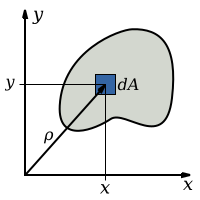
The second moment of area for an arbitrary shape with respect to an arbitrary axis is defined as
For example, when the desired reference axis is the x-axis the second moment of area, (often denoted as ) can be computed in Cartesian coordinates as
Parallel axis theorem
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
It is often easier to derive the second moment of area with respect to its centroidal axis, . However, it may be necessary to calculate the second moment of area with respect to a different, parallel axis, say the axis. The parallel axis theorem states
where
A similar statement can be made about the axis and the parallel centroidal axis. Or, in general, any centroidal axis and a parallel axis.
Perpendicular axis theorem
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
For the simplicity of calculation, it is often desired to define the polar moment of inertia (with respect to a perpendicular axis) in terms of two area moments of inertia (both with respect to in-plane axes). The simplest case relates to and .
This relationship relies on the Pythagorean theorem which relates and to and on the linearity of integration.
Composite shapes
For more complex areas, it is often easier to divide the area into a series of "simpler" shapes. The second moment of area for the entire shape is the sum of the second moment of areas of all of its parts about a common axis. This can include shapes that are "missing" (i.e. holes, hollow shapes, etc.), in which case the second moment of area of the "missing" areas are subtracted, rather than added. In other words, the second moment of area of "missing" parts are considered negative for the method of composite shapes.
Examples
See list of area moments of inertia for other cross-sections.
Rectangle with centroid at the origin
Consider a rectangle with base and height whose centroid is located at the origin. represents the second moment of area with respect to the x-axis; represents the second moment of area with respect to the y-axis; represents the polar moment of inertia with respect to the z-axis.

Annulus centered at origin

Consider an annulus whose center is at the origin, outside radius is , and inside radius is . Because of the symmetry of the annulus, the centroid also lies at the origin. We can determine the polar moment of inertia, , about the axis by the method of composite shapes. This polar moment of inertia is equivalent to the polar moment of inertia of a circle with radius minus the polar moment of inertia of a circle with radius , both centered at the origin. First, let us derive the polar moment of inertia of a circle with radius with respect to the origin. In this case, it is easier to directly calculate as we already have , which has both an and component. Instead of calculating and as done in the previous section, we shall calculate directly using Polar Coordinates.
Now, the polar moment of inertia about the axis for an annulus is simply, as stated above, the difference of the second moments of area of a circle with radius and a circle with radius .
Alternatively, we could change the limits on the integral the first time around to reflect the fact that there is a hole. This would be done like this.
Any polygon
The second moment of area for any simple polygon on the XY-plane can be computed in general by summing contributions from each segment of the polygon (method of composite shapes)(order of iteration along the poligon vertex gives sign to the value calculated).

where : are the coordinates of any polygon vertex[1] - www.mecsym.org
See also
- List of area moments of inertia
- List of moments of inertia
- Moment of inertia
- Parallel axis theorem
- Perpendicular axis theorem
- Radius of gyration
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
- ↑ Mechanical Symmetry by Joaquin Obregon - December 2012 - ISBN 978 1 4772 3372 6


































![{\displaystyle J_{z}=\iint r^{2}\,dA=\int _{0}^{2\pi }\int _{r_{i}}^{r_{o}}r^{2}\left(r\,dr\,d\theta \right)=\int _{0}^{2\pi }\int _{r_{i}}^{r_{o}}r^{3}\,dr\,d\theta =\int _{0}^{2\pi }\left[{\frac {r_{o}^{4}}{4}}-{\frac {r_{i}^{4}}{4}}\right]\,d\theta ={\frac {\pi }{2}}\left(r_{o}^{4}-r_{i}^{4}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e37b38137006d02363d43da87160c343b08a03cf)



