Kerr–Newman metric: Difference between revisions
en>Helpful Pixie Bot m ISBNs (Build KE) |
en>Maschen →Mathematical form: match symbols to formulae, bold usually means vectors, remove unneeded quotation marks around each symbol and abrupt indentations, other tidyup tweaks |
||
| Line 1: | Line 1: | ||
In the [[mathematics|mathematical]] field of [[graph theory]], the '''Laplacian matrix''', sometimes called '''admittance matrix''', '''Kirchhoff matrix''' or '''discrete Laplacian''', is a [[matrix (mathematics)|matrix]] representation of a [[graph (mathematics)|graph]]. Together with [[Kirchhoff's theorem]], it can be used to calculate the number of [[spanning tree (mathematics)|spanning tree]]s for a given graph. The Laplacian matrix can be used to find many other properties of the graph; see [[spectral graph theory]]. [[Cheeger_constant#Cheeger.27s_inequality|Cheeger's inequality]] from [[Riemannian geometry]] has a discrete analogue involving the Laplacian matrix; this is perhaps the most important theorem in spectral graph theory and one of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian. | |||
==Definition== | |||
Given a [[simple graph]] ''G'' with ''n'' vertices, its Laplacian matrix <math>L:=(\ell_{i,j})_{n \times n}</math> is defined as:<ref name="mathworld">{{MathWorld |urlname=LaplacianMatrix |title=Laplacian Matrix}}</ref> | |||
: <math> | |||
L = D - A. | |||
</math> | |||
That is, it is the difference of the [[degree matrix]] ''D'' and the [[adjacency matrix]] ''A'' of the graph. | |||
In the case of [[directed graph]]s, either the [[degree (graph theory)|indegree or outdegree]] might be used, depending on the application. | |||
From the definition it follows that: | |||
: <math>\ell_{i,j}:= | |||
\begin{cases} | |||
\deg(v_i) & \mbox{if}\ i = j \\ | |||
-1 & \mbox{if}\ i \neq j\ \mbox{and}\ v_i \mbox{ is adjacent to } v_j \\ | |||
0 & \mbox{otherwise} | |||
\end{cases} | |||
</math> | |||
where deg(''v<sub>i</sub>'') is degree of the vertex ''i''. | |||
The [[#Symmetric normalized Laplacian|normalized Laplacian matrix]] is defined as:<ref name="mathworld" /> | |||
:<math>\ell_{i,j}:= | |||
\begin{cases} | |||
1 & \mbox{if}\ i = j\ \mbox{and}\ \deg(v_i) \neq 0\\ | |||
-\frac{1}{\sqrt{\deg(v_i)\deg(v_j)}} & \mbox{if}\ i \neq j\ \mbox{and}\ v_i \mbox{ is adjacent to } v_j \\ | |||
0 & \mbox{otherwise}. | |||
\end{cases} | |||
</math> | |||
==Example== | |||
Here is a simple example of a labeled graph and its Laplacian matrix. | |||
{|class="wikitable" | |||
![[Labeled graph]] | |||
!Degree matrix | |||
!Adjacency matrix | |||
!Laplacian matrix | |||
|- | |||
|[[image:6n-graf.svg|175px]] | |||
|<math>\left(\begin{array}{rrrrrr} | |||
2 & 0 & 0 & 0 & 0 & 0\\ | |||
0 & 3 & 0 & 0 & 0 & 0\\ | |||
0 & 0 & 2 & 0 & 0 & 0\\ | |||
0 & 0 & 0 & 3 & 0 & 0\\ | |||
0 & 0 & 0 & 0 & 3 & 0\\ | |||
0 & 0 & 0 & 0 & 0 & 1\\ | |||
\end{array}\right)</math> | |||
|<math>\left(\begin{array}{rrrrrr} | |||
0 & 1 & 0 & 0 & 1 & 0\\ | |||
1 & 0 & 1 & 0 & 1 & 0\\ | |||
0 & 1 & 0 & 1 & 0 & 0\\ | |||
0 & 0 & 1 & 0 & 1 & 1\\ | |||
1 & 1 & 0 & 1 & 0 & 0\\ | |||
0 & 0 & 0 & 1 & 0 & 0\\ | |||
\end{array}\right)</math> | |||
|<math>\left(\begin{array}{rrrrrr} | |||
2 & -1 & 0 & 0 & -1 & 0\\ | |||
-1 & 3 & -1 & 0 & -1 & 0\\ | |||
0 & -1 & 2 & -1 & 0 & 0\\ | |||
0 & 0 & -1 & 3 & -1 & -1\\ | |||
-1 & -1 & 0 & -1 & 3 & 0\\ | |||
0 & 0 & 0 & -1 & 0 & 1\\ | |||
\end{array}\right)</math> | |||
|} | |||
==Properties== | |||
For a graph ''G'' and its Laplacian matrix ''L'' with [[eigenvalues]] <math>\lambda_0 \le \lambda_1 \le \cdots \le \lambda_{n-1}</math>: | |||
* ''L'' is always [[positive-definite matrix|positive-semidefinite]] (<math>\forall i, \lambda_i \ge 0; \lambda_0 = 0</math>). This is verified in the following [[#Incidence matrix | Incidence matrix]] section. | |||
* The number of times 0 appears as an eigenvalue in the Laplacian is the number of [[Connected component (graph theory)|connected components]] in the graph. | |||
* ''L'' is an [[M-matrix]]. | |||
* <math>\lambda_0</math> is always 0 because every Laplacian matrix has an eigenvector <math>\mathbf{v}_0=[1,1,\dots,1]</math> that, for each row, adds the corresponding node's degree (from the diagonal) to a "-1" for each neighbor so that <math>L \mathbf{v}_0 = 0 .</math> | |||
* The smallest non-zero eigenvalue of ''L'' is called the [[spectral gap]]. | |||
* The second smallest eigenvalue of ''L'' is the [[algebraic connectivity]] (or [[Fiedler value]]) of ''G''. | |||
* The [[Laplacian]] is an operator on the function of g. When G is k-regular, | |||
:<math>\ell = I-\frac{1}{k} A</math>, | |||
where A is the adjacency matrix of G and I is an identity matrix. All matrices are n × n where n is the number of vertices in G. | |||
* For a graph with multiple [[Connected component (graph theory) | connected components]], ''L'' is a [[Block matrix#Block diagonal matrices | block diagonal]] matrix, where each block is the respective Laplacian matrix for each component. | |||
== Incidence matrix == | |||
Define an <math>|e|</math> x <math>|v|</math> oriented [[incidence matrix]] ''M'' with element ''M''<sub>''ev''</sub> for edge ''e'' (connecting vertex ''i'' and ''j'', with ''i'' > ''j'') and vertex ''v'' given by | |||
:<math>M_{ev} = \left\{ \begin{array}{rl}1, & \text{if}\,v=i\\-1, & \text{if}\,v=j\\0, & \text{otherwise}.\end{array}\right.</math> | |||
Then the Laplacian matrix ''L'' satisfies | |||
:<math>L = M^\text{T} M\,,</math> | |||
where <math>M^\text{T}</math> is the [[transpose|matrix transpose]] of ''M''. | |||
Now consider an eigendecomposition of <math>L</math>, with unit-norm eigenvectors <math>\mathbf{v}_i</math> and corresponding eigenvalues <math>\lambda_i</math>: | |||
:<math> | |||
\begin{align} | |||
\lambda_i & = \mathbf{v}_i^T L \mathbf{v}_i \\ | |||
& = \mathbf{v}_i^T M^T M \mathbf{v}_i \\ | |||
& = (M \mathbf{v}_i)^T (M \mathbf{v}_i). \\ | |||
\end{align} | |||
</math> | |||
Because <math>\lambda_i</math> can be written as the inner product of the vector <math>M \mathbf{v}_i</math> with itself, this shows that <math>\lambda_i \ge 0</math> and so the eigenvalues of <math>L</math> are all non-negative. | |||
== Deformed Laplacian == | |||
The '''deformed Laplacian''' is commonly defined as | |||
:<math>\Delta(s)=I-sA+s^2(D-I)</math> | |||
where ''I'' is the unit matrix, ''A'' is the adjacency matrix, and ''D'' is the degree matrix, and ''s'' is a (complex-valued) number. Note that the standard Laplacian is just <math>\Delta(1)</math>. | |||
== Symmetric normalized Laplacian == | |||
The '''symmetric normalized Laplacian''' (a.k.a. normalized Laplacian) is defined as | |||
: <math>L^{norm}:=I-D^{-1/2}AD^{-1/2}</math> | |||
where ''A'' is the adjacency matrix and ''D'' is the degree matrix. Since the degree matrix ''D'' is diagonal, its reciprocal square root <math>D^{-1/2}</math> is simply defined as a diagonal matrix, having diagonal entries which are the reciprocals of the positive square roots of the corresponding positive diagonal entries of ''D''. The symmetric normalized Laplacian is a symmetric matrix. | |||
:<math>L^{norm} = S S^{*}</math>, | |||
where S is the matrix whose rows are indexed by the vertices and whose columns are indexed by the edges of G such that each column corresponding to an edge e = {u, v} has an entry <math>\frac{1}{\sqrt d_{u}}</math> in the row corresponding to u, an entry <math>-\frac{1}{\sqrt d_{v}}</math> in the row corresponding to v, and has 0 entries elsewhere. (Note: <math>S^{*}</math> denotes the transpose of S). | |||
The symmetric normalized Laplacian can also be written as | |||
: <math>L^{norm}=I-D^{-1/2}AD^{-1/2} = D^{-1/2} L D^{-1/2}.</math> | |||
All eigenvalues of the normalized Laplacian are real and non-negative. In fact,if λ is an eigenvalue of L, then 0 ≤ λ ≤ 2. These eigenvalues (known as spectra of the normalized Laplacian) relate well to other graph invariants for general graphs.<ref>{{cite book | |||
| last = Chung | |||
| first = Fan | |||
| title = Spectral Graph Theory | |||
| url = http://www.math.ucsd.edu/~fan/research/revised.html | |||
| year = 1992, revised 1997 | |||
| publisher = American Mathematical Society | |||
| isbn = 0821803158 | |||
}}</ref> | |||
Since <math>L^{norm}</math> is symmetric, its eigenvalues are real and non-negative. We can use its characterization in terms of [[Rayleigh quotient]] of <math>L^{norm}</math>. | |||
Let g be an arbitrary function which assigns to each vertex v of G a real value g(v). We can treat g as a column vector. | |||
:<math> | |||
\begin{align} | |||
\frac{g,L^{norm}_{g}}{g, g} & = \frac{g, D^{-1/2} L D^{-1/2} g}{g,g} \\ | |||
& =\frac{f, Lf}{D^{1/2} f, D^{1/2} f} \\ | |||
& =\frac{\sum_{u~v}(f(u) - f(v) )^2}{\sum_{v} f(v)^2 d_{v}}, | |||
\end{align} | |||
</math> | |||
where <math> g = D^{1/2} f</math> and <math>\sum_{u~v}</math> denotes the sum over all unordered pairs {u,v} for which u and v are adjacent. <math>\sum_{u,v}(f(u) - f(v) )^2</math> is called the [[Dirichlet sum]] of G. The left hand side of the equation is Rayleigh quotient. | |||
The eigenvalues of <math>L^{norm}</math> by <math>0 = \lambda_0\le\lambda_1\le\cdots\lambda_{n-1}</math>. the set of <math>\lambda_i</math> is usually called the ''spectrum of <math>L^{norm}</math>'' Let '''1''' be the function which assumes the value 1 on each vertex. Then <math>D^{1/2} 1</math> is an eigenfunction of <math>L^{norm}</math> with eigenvalue 0. | |||
<ref>{{cite book|last=Chung|first=Fan R.K.|title=Spectral graph theory|year=1997|publisher=American Math. Soc.|location=Providence, RI|isbn=0-8218-0315-8|edition=Repr. with corr., 2. [pr.]}}</ref> | |||
== Random walk normalized Laplacian == | |||
The '''random walk normalized Laplacian''' is defined as | |||
: <math>T:=D^{-1}A</math> | |||
where ''A'' is the adjacency matrix and ''D'' is the degree matrix. Since the degree matrix ''D'' is diagonal, its inverse <math>D^{-1}</math> is simply defined as a diagonal matrix, having diagonal entries which are the reciprocals of the corresponding positive diagonal entries of ''D''. The name of this operator comes from the fact that, indeed, <math>T</math> is the transition matrix of a standard random walk on the given graph. | |||
One can check that | |||
: <math>T=D^{-\frac12} \left(I-L^{norm}\right) D^{\frac12}</math>, | |||
i.e., <math>T</math> is similar to a scalar perturbation of the normalized Laplacian <math>L^{norm}</math>. For this reason, even if <math>T</math> is in general not hermitian, it has real eigenvalues. Indeed, its eigenvalues agree with those of <math>L^{norm}</math> (which is hermitian), up to a mirroring in the point <math>1/2</math>. | |||
=== Random walks on graphs === | |||
As an aside about [[Random walk#Random walk on graphs | random walks on graphs]], consider a simple [[Graph (mathematics)#Undirected graph | undirected graph]]. Consider the probability that a walk is at a vertex ''i'' at time ''t'' comes from vertex ''j'' at time ''t-1'' (assuming a uniform chance of taking a step along any of the edges attached to vertex ''j''): | |||
: <math> | |||
p_i(t) = \sum_j \frac{A_{ij}}{deg(v_j)} p_j(t-1), | |||
</math> | |||
or in matrix-vector notation: | |||
:<math> | |||
p(t) = A D^{-1} p(t-1). | |||
</math> | |||
(At equilibrium where <math>t\rightarrow \infty</math>, this is written as <math>p = A D^{-1} p </math>). | |||
We can rewrite this relation as | |||
:<math> | |||
\begin{align} | |||
D^{-\frac12} p(t) &= D^{-\frac12} A D^{-1} p(t-1) \\ | |||
& = \left[ D^{-\frac12} A D^{-\frac12} \right] D^{-\frac12} p(t-1). | |||
\end{align} | |||
</math> | |||
<math>A_{reduced} \equiv D^{-\frac12} A D^{-\frac12}</math> is a symmetric matrix called the '''reduced adjacency matrix'''. So, taking steps on this random walk requires repeated multiplication of <math>A_{reduced}</math>, which is a simple operation because <math>A_{reduced}</math> is symmetric. | |||
== Interpretation as the discrete Laplace operator == | |||
The Laplacian matrix can be interpreted as a matrix representation of a particular case of the negative [[discrete Laplace operator]]. Such an interpretation allows one, e.g., to generalise the Laplacian matrix to the case of graphs with an infinite number of vertices and edges, leading to a Laplacian matrix of an infinite size. | |||
To expand upon this, we can describe the change of some element <math>\phi_i</math> (with some constant ''k'') as | |||
:<math> | |||
\begin{align} | |||
\frac{d \phi_i}{d t} & = -k \sum_j A_{ij} (\phi_i - \phi_j) \\ | |||
& = -k \phi_i \sum_j A_{ij} + k \sum_j A_{ij} \phi_j \\ | |||
& = - k \phi_i \ deg(v_i) + k \sum_j A_{ij} \phi_j \\ | |||
& = - k \sum_j (\delta_{ij} \ deg(v_i) - A_{ij} ) \phi_j \\ | |||
& = -k \sum_j (\ell_{ij} ) \phi_j. | |||
\end{align} | |||
</math> | |||
In matrix-vector notation, | |||
:<math> | |||
\begin{align} | |||
\frac{d \phi}{d t} & = -k(D-A)\phi \\ | |||
& = -k L \phi, | |||
\end{align} | |||
</math> | |||
which gives | |||
:<math> | |||
\begin{align} | |||
\frac{d \phi}{d t} + kL\phi = 0. | |||
\end{align} | |||
</math> | |||
Notice that this equation takes the same form as the [[heat equation]], where the matrix ''L'' is replacing the Laplacian operator <math>\nabla^2</math>; hence, the "graph Laplacian". | |||
To find a solution to this differential equation, apply standard techniques for solving a first-order [[matrix differential equation]]. That is, write <math>\phi</math> as a linear combination of eigenvectors <math>\mathbf{v}_i</math> of ''L'' (so that <math>L\mathbf{v}_i = \lambda_i \mathbf{v}_i</math>), with time-dependent coefficients <math>c_i(t)</math>: | |||
:<math> | |||
\begin{align} | |||
\phi = \sum_i c_i \mathbf{v}_i. | |||
\end{align} | |||
</math> | |||
Plugging into the original expression (note that we will use the fact that because ''L'' is a symmetric matrix, its unit-norm eigenvectors <math>\mathbf{v}_i</math> are orthogonal): | |||
:<math> | |||
\begin{align} | |||
\frac{d (\sum_i c_i \mathbf{v}_i)}{d t} + kL(\sum_i c_i \mathbf{v}_i) & = 0 \\ | |||
\sum_i \left[ \frac{d c_i}{d t} \mathbf{v}_i + k c_i L \mathbf{v}_i \right] & = \\ | |||
\sum_i \left[ \frac{d c_i}{d t} \mathbf{v}_i + k c_i \lambda_i \mathbf{v}_i \right] & = \\ | |||
\frac{d c_i}{d t} + k \lambda_i c_i & = 0, \\ | |||
\end{align} | |||
</math> | |||
whose solution is | |||
:<math> | |||
\begin{align} | |||
c_i(t) = c_i(0) \exp(-k \lambda_i t). | |||
\end{align} | |||
</math> | |||
As shown before, the eigenvalues <math>\lambda_i</math> of ''L'' are non-negative, showing that the solution to the diffusion equation approaches an equilibrium, because it only exponentially decays or remains constant. This also shows that given <math>\lambda_i</math> and the initial condition <math>c_i(0)</math>, the solution at any time ''t'' can be found.<ref>{{cite book | |||
| last = Newman | |||
| first = Mark | |||
| title = Networks: An Introduction | |||
| year = 2010 | |||
| publisher = Oxford University Press | |||
| isbn = 0199206651 | |||
}}</ref> | |||
To find <math>c_i(0)</math> for each <math>i</math> in terms of the overall initial condition <math>c(0)</math>, simply project <math>c(0)</math> onto the unit-norm eigenvectors <math>\mathbf{v}_i</math>; | |||
<math>c_i(0) = \langle c(0), \mathbf{v}_i \rangle </math>. | |||
In the case of undirected graphs, this works because <math>L</math> is symmetric, and by the [[spectral theorem]], its eigenvectors are all orthogonal. So the projection onto the eigenvectors of <math>L</math> is simply an orthogonal coordinate transformation of the initial condition to a set of coordinates which decay exponentially and independently of each other. | |||
=== Equilibrium Behavior === | |||
To understand <math>\lim_{t \to \infty}\phi(t)</math>, note that the only terms <math> c_i(t) = c_i(0) \exp(-k \lambda_i t)</math> that remain are those where <math>\lambda_i = 0</math>, since | |||
<math>\lim_{x \to \infty} \exp(-k \lambda_i t) = \left\{ \begin{array}{rlr}1 & \text{if} &\lambda_i > 0 \\ 0 & \text{if} & \lambda_i = 0 \end{array} \right\} </math> | |||
In other words, the equilibrium state of the system is determined completely by the [[Kernel_(linear_algebra)|kernel]] of <math>L</math>. | |||
Since by definition, <math>\sum_{j}L_{ij} = 0</math>, the vector <math>\mathbf{v}^1</math> of all ones is in the kernel. Note also that if there are <math>k</math> disjoint [[Connected_component_(graph_theory)|connected components]] in the graph, then this vector of all ones can be split into the sum of <math>k</math> independent <math>\lambda = 0</math> eigenvectors of ones and zeros, where each connected component corresponds to an eigenvector with ones at the elements in the connected component and zeros elsewhere. | |||
The consequence of this is that for a given initial condition <math>c(0)</math> for a graph with <math>N</math> vertices | |||
<math>\lim_{t \to \infty}\phi(t) = \langle c(0), \mathbf{v^1} \rangle \mathbf{v^1} </math> | |||
where | |||
<math>\mathbf{v^1} = \frac{1}{\sqrt{N}} [1, 1, ..., 1] </math> | |||
For each vertex <math>j</math> in the graph, this can be rewritten as | |||
<math> \lim_{t \to \infty}\phi(t)_j = \frac{1}{N} \sum_{i = 1}^N c(0)_i </math> | |||
In other words, at steady state, the value of <math>\phi</math> converges to the same value at each of the vertices of the graph, which is the average of the initial values at all of the vertices. Since this is the solution to the heat diffusion equation, this makes perfect sense intuitively. We expect that neighboring elements in the graph will exchange energy until that energy is spread out evenly throughout all of the elements that are connected to each other. | |||
=== Example of the Operator on a Grid === | |||
[[File:Graph Laplacian Diffusion Example.gif|thumb|This GIF shows the progression of diffusion, as solved by the graph laplacian technique. A graph is constructed over a grid, where each pixel in the graph is connected to its 8 bordering pixels. Values in the image then diffuse smoothly to their neighbors over time via these connections. This particular image starts off with three strong point values which spill over to their neighbors slowly. The whole system eventually settles out to the same value at equilibrium.]] | |||
This section shows an example of a function <math>\phi</math> diffusing over time through a graph. The graph in this example is constructed on a 2D discrete grid, with points on the grid connected to their eight neighbors. Three initial points are specified to have a positive value, while the rest of the values in the grid are zero. Over time, the exponential decay acts to distribute the values at these points evenly throughout the entire grid. | |||
The complete Matlab source code that was used to generate this animation is provided below. It shows the process of specifying initial conditions, projecting these initial conditions onto the eigenvalues of the Laplacian Matrix, and simulating the exponential decay of these projected initial conditions. | |||
<source lang=matlab> | |||
N = 20;%The number of pixels along a dimension of the image | |||
A = zeros(N, N);%The image | |||
Adj = zeros(N*N, N*N);%The adjacency matrix | |||
%Use 8 neighbors, and fill in the adjacency matrix | |||
dx = [-1, 0, 1, -1, 1, -1, 0, 1]; | |||
dy = [-1, -1, -1, 0, 0, 1, 1, 1]; | |||
for x = 1:N | |||
for y = 1:N | |||
index = (x-1)*N + y; | |||
for ne = 1:length(dx) | |||
newx = x + dx(ne); | |||
newy = y + dy(ne); | |||
if newx > 0 && newx <= N && newy > 0 && newy <= N | |||
index2 = (newx-1)*N + newy; | |||
Adj(index, index2) = 1; | |||
end | |||
end | |||
end | |||
end | |||
%%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL | |||
%%%EQUATION | |||
Deg = diag(sum(Adj, 2));%Compute the degree matrix | |||
L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices | |||
[V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix | |||
D = diag(D); | |||
%Initial condition (place a few large positive values around and | |||
%make everything else zero) | |||
C0 = zeros(N, N); | |||
C0(2:5, 2:5) = 5; | |||
C0(10:15, 10:15) = 10; | |||
C0(2:5, 8:13) = 7; | |||
C0 = C0(:); | |||
C0V = V'*C0;%Transform the initial condition into the coordinate system | |||
%of the eigenvectors | |||
for t = 0:0.05:5 | |||
%Loop through times and decay each initial component | |||
Phi = C0V.*exp(-D*t);%Exponential decay for each component | |||
Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system | |||
Phi = reshape(Phi, N, N); | |||
%Display the results and write to GIF file | |||
imagesc(Phi); | |||
caxis([0, 10]); | |||
title(sprintf('Diffusion t = %3f', t)); | |||
frame = getframe(1); | |||
im = frame2im(frame); | |||
[imind, cm] = rgb2ind(im, 256); | |||
if t == 0 | |||
imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1); | |||
else | |||
imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1); | |||
end | |||
end | |||
</source> | |||
== As an approximation to the negative continuous Laplacian == | |||
The graph Laplacian matrix can be further viewed as a matrix form of an approximation to the '''negative''' [[Laplacian]] operator obtained by the [[finite difference method]] {{Citation needed|date=March 2012}}. In this interpretation, every graph vertex is treated as a grid point; the local connectivity of the vertex determines the finite difference approximation [[stencil (numerical analysis)|stencil]] at this grid point, the grid size is always one for every edge, and there are no constraints on any grid points, which corresponds to the case of the homogeneous [[Neumann boundary condition]], i.e., free boundary. | |||
== See also == | |||
*[[Stiffness matrix]] | |||
*[[Resistance distance]] | |||
== References == | |||
{{reflist}} | |||
T. Sunada, Discrete geometric analysis, ''Proceedings of Symposia in Pure Mathematics,'' (ed. by P. Exner, J. P. Keating, P. Kuchment, T. Sunada, A. Teplyaev), '''77''' (2008), 51-86. | |||
[[Category:Algebraic graph theory]] | |||
[[Category:Matrices]] | |||
Revision as of 23:29, 13 December 2013
In the mathematical field of graph theory, the Laplacian matrix, sometimes called admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. Together with Kirchhoff's theorem, it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be used to find many other properties of the graph; see spectral graph theory. Cheeger's inequality from Riemannian geometry has a discrete analogue involving the Laplacian matrix; this is perhaps the most important theorem in spectral graph theory and one of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian.
Definition
Given a simple graph G with n vertices, its Laplacian matrix is defined as:[1]
That is, it is the difference of the degree matrix D and the adjacency matrix A of the graph. In the case of directed graphs, either the indegree or outdegree might be used, depending on the application.
From the definition it follows that:
where deg(vi) is degree of the vertex i.
The normalized Laplacian matrix is defined as:[1]
Example
Here is a simple example of a labeled graph and its Laplacian matrix.
| Labeled graph | Degree matrix | Adjacency matrix | Laplacian matrix |
|---|---|---|---|
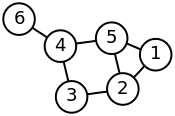
|
Properties
For a graph G and its Laplacian matrix L with eigenvalues :
- L is always positive-semidefinite (). This is verified in the following Incidence matrix section.
- The number of times 0 appears as an eigenvalue in the Laplacian is the number of connected components in the graph.
- L is an M-matrix.
- is always 0 because every Laplacian matrix has an eigenvector that, for each row, adds the corresponding node's degree (from the diagonal) to a "-1" for each neighbor so that
- The smallest non-zero eigenvalue of L is called the spectral gap.
- The second smallest eigenvalue of L is the algebraic connectivity (or Fiedler value) of G.
- The Laplacian is an operator on the function of g. When G is k-regular,
where A is the adjacency matrix of G and I is an identity matrix. All matrices are n × n where n is the number of vertices in G.
- For a graph with multiple connected components, L is a block diagonal matrix, where each block is the respective Laplacian matrix for each component.
Incidence matrix
Define an x oriented incidence matrix M with element Mev for edge e (connecting vertex i and j, with i > j) and vertex v given by
Then the Laplacian matrix L satisfies
where is the matrix transpose of M.
Now consider an eigendecomposition of , with unit-norm eigenvectors and corresponding eigenvalues :
Because can be written as the inner product of the vector with itself, this shows that and so the eigenvalues of are all non-negative.
Deformed Laplacian
The deformed Laplacian is commonly defined as
where I is the unit matrix, A is the adjacency matrix, and D is the degree matrix, and s is a (complex-valued) number. Note that the standard Laplacian is just .
Symmetric normalized Laplacian
The symmetric normalized Laplacian (a.k.a. normalized Laplacian) is defined as
where A is the adjacency matrix and D is the degree matrix. Since the degree matrix D is diagonal, its reciprocal square root is simply defined as a diagonal matrix, having diagonal entries which are the reciprocals of the positive square roots of the corresponding positive diagonal entries of D. The symmetric normalized Laplacian is a symmetric matrix.
where S is the matrix whose rows are indexed by the vertices and whose columns are indexed by the edges of G such that each column corresponding to an edge e = {u, v} has an entry in the row corresponding to u, an entry in the row corresponding to v, and has 0 entries elsewhere. (Note: denotes the transpose of S).
The symmetric normalized Laplacian can also be written as
All eigenvalues of the normalized Laplacian are real and non-negative. In fact,if λ is an eigenvalue of L, then 0 ≤ λ ≤ 2. These eigenvalues (known as spectra of the normalized Laplacian) relate well to other graph invariants for general graphs.[2]
Since is symmetric, its eigenvalues are real and non-negative. We can use its characterization in terms of Rayleigh quotient of .
Let g be an arbitrary function which assigns to each vertex v of G a real value g(v). We can treat g as a column vector.
where and denotes the sum over all unordered pairs {u,v} for which u and v are adjacent. is called the Dirichlet sum of G. The left hand side of the equation is Rayleigh quotient.
The eigenvalues of by . the set of is usually called the spectrum of Let 1 be the function which assumes the value 1 on each vertex. Then is an eigenfunction of with eigenvalue 0.
Random walk normalized Laplacian
The random walk normalized Laplacian is defined as
where A is the adjacency matrix and D is the degree matrix. Since the degree matrix D is diagonal, its inverse is simply defined as a diagonal matrix, having diagonal entries which are the reciprocals of the corresponding positive diagonal entries of D. The name of this operator comes from the fact that, indeed, is the transition matrix of a standard random walk on the given graph.
One can check that
i.e., is similar to a scalar perturbation of the normalized Laplacian . For this reason, even if is in general not hermitian, it has real eigenvalues. Indeed, its eigenvalues agree with those of (which is hermitian), up to a mirroring in the point .
Random walks on graphs
As an aside about random walks on graphs, consider a simple undirected graph. Consider the probability that a walk is at a vertex i at time t comes from vertex j at time t-1 (assuming a uniform chance of taking a step along any of the edges attached to vertex j):
or in matrix-vector notation:
(At equilibrium where , this is written as ).
We can rewrite this relation as
is a symmetric matrix called the reduced adjacency matrix. So, taking steps on this random walk requires repeated multiplication of , which is a simple operation because is symmetric.
Interpretation as the discrete Laplace operator
The Laplacian matrix can be interpreted as a matrix representation of a particular case of the negative discrete Laplace operator. Such an interpretation allows one, e.g., to generalise the Laplacian matrix to the case of graphs with an infinite number of vertices and edges, leading to a Laplacian matrix of an infinite size.
To expand upon this, we can describe the change of some element (with some constant k) as
In matrix-vector notation,
which gives
Notice that this equation takes the same form as the heat equation, where the matrix L is replacing the Laplacian operator ; hence, the "graph Laplacian".
To find a solution to this differential equation, apply standard techniques for solving a first-order matrix differential equation. That is, write as a linear combination of eigenvectors of L (so that ), with time-dependent coefficients :
Plugging into the original expression (note that we will use the fact that because L is a symmetric matrix, its unit-norm eigenvectors are orthogonal):
whose solution is
As shown before, the eigenvalues of L are non-negative, showing that the solution to the diffusion equation approaches an equilibrium, because it only exponentially decays or remains constant. This also shows that given and the initial condition , the solution at any time t can be found.[4]
To find for each in terms of the overall initial condition , simply project onto the unit-norm eigenvectors ;
In the case of undirected graphs, this works because is symmetric, and by the spectral theorem, its eigenvectors are all orthogonal. So the projection onto the eigenvectors of is simply an orthogonal coordinate transformation of the initial condition to a set of coordinates which decay exponentially and independently of each other.
Equilibrium Behavior
To understand , note that the only terms that remain are those where , since
In other words, the equilibrium state of the system is determined completely by the kernel of . Since by definition, , the vector of all ones is in the kernel. Note also that if there are disjoint connected components in the graph, then this vector of all ones can be split into the sum of independent eigenvectors of ones and zeros, where each connected component corresponds to an eigenvector with ones at the elements in the connected component and zeros elsewhere.
The consequence of this is that for a given initial condition for a graph with vertices
where
For each vertex in the graph, this can be rewritten as
In other words, at steady state, the value of converges to the same value at each of the vertices of the graph, which is the average of the initial values at all of the vertices. Since this is the solution to the heat diffusion equation, this makes perfect sense intuitively. We expect that neighboring elements in the graph will exchange energy until that energy is spread out evenly throughout all of the elements that are connected to each other.
Example of the Operator on a Grid

This section shows an example of a function diffusing over time through a graph. The graph in this example is constructed on a 2D discrete grid, with points on the grid connected to their eight neighbors. Three initial points are specified to have a positive value, while the rest of the values in the grid are zero. Over time, the exponential decay acts to distribute the values at these points evenly throughout the entire grid.
The complete Matlab source code that was used to generate this animation is provided below. It shows the process of specifying initial conditions, projecting these initial conditions onto the eigenvalues of the Laplacian Matrix, and simulating the exponential decay of these projected initial conditions.
N = 20;%The number of pixels along a dimension of the image
A = zeros(N, N);%The image
Adj = zeros(N*N, N*N);%The adjacency matrix
%Use 8 neighbors, and fill in the adjacency matrix
dx = [-1, 0, 1, -1, 1, -1, 0, 1];
dy = [-1, -1, -1, 0, 0, 1, 1, 1];
for x = 1:N
for y = 1:N
index = (x-1)*N + y;
for ne = 1:length(dx)
newx = x + dx(ne);
newy = y + dy(ne);
if newx > 0 && newx <= N && newy > 0 && newy <= N
index2 = (newx-1)*N + newy;
Adj(index, index2) = 1;
end
end
end
end
%%%BELOW IS THE KEY CODE THAT COMPUTES THE SOLUTION TO THE DIFFERENTIAL
%%%EQUATION
Deg = diag(sum(Adj, 2));%Compute the degree matrix
L = Deg - Adj;%Compute the laplacian matrix in terms of the degree and adjacency matrices
[V, D] = eig(L);%Compute the eigenvalues/vectors of the laplacian matrix
D = diag(D);
%Initial condition (place a few large positive values around and
%make everything else zero)
C0 = zeros(N, N);
C0(2:5, 2:5) = 5;
C0(10:15, 10:15) = 10;
C0(2:5, 8:13) = 7;
C0 = C0(:);
C0V = V'*C0;%Transform the initial condition into the coordinate system
%of the eigenvectors
for t = 0:0.05:5
%Loop through times and decay each initial component
Phi = C0V.*exp(-D*t);%Exponential decay for each component
Phi = V*Phi;%Transform from eigenvector coordinate system to original coordinate system
Phi = reshape(Phi, N, N);
%Display the results and write to GIF file
imagesc(Phi);
caxis([0, 10]);
title(sprintf('Diffusion t = %3f', t));
frame = getframe(1);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if t == 0
imwrite(imind, cm, 'out.gif', 'gif', 'Loopcount', inf, 'DelayTime', 0.1);
else
imwrite(imind, cm, 'out.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);
end
end
As an approximation to the negative continuous Laplacian
The graph Laplacian matrix can be further viewed as a matrix form of an approximation to the negative Laplacian operator obtained by the finite difference method Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park.. In this interpretation, every graph vertex is treated as a grid point; the local connectivity of the vertex determines the finite difference approximation stencil at this grid point, the grid size is always one for every edge, and there are no constraints on any grid points, which corresponds to the case of the homogeneous Neumann boundary condition, i.e., free boundary.
See also
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro. T. Sunada, Discrete geometric analysis, Proceedings of Symposia in Pure Mathematics, (ed. by P. Exner, J. P. Keating, P. Kuchment, T. Sunada, A. Teplyaev), 77 (2008), 51-86.
- ↑ 1.0 1.1
I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog. - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534










![{\mathbf {v}}_{0}=[1,1,\dots ,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa72fc3006869afba2cfe0b85587220dbc5526e)






































![{\begin{aligned}D^{{-{\frac 12}}}p(t)&=D^{{-{\frac 12}}}AD^{{-1}}p(t-1)\\&=\left[D^{{-{\frac 12}}}AD^{{-{\frac 12}}}\right]D^{{-{\frac 12}}}p(t-1).\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abe751ed7f92c8ec04b8dc78dc7c981651152a0a)











![{\displaystyle {\begin{aligned}{\frac {d(\sum _{i}c_{i}\mathbf {v} _{i})}{dt}}+kL(\sum _{i}c_{i}\mathbf {v} _{i})&=0\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}L\mathbf {v} _{i}\right]&=\\\sum _{i}\left[{\frac {dc_{i}}{dt}}\mathbf {v} _{i}+kc_{i}\lambda _{i}\mathbf {v} _{i}\right]&=\\{\frac {dc_{i}}{dt}}+k\lambda _{i}c_{i}&=0,\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b387f277f45882e4ffe5742d3471ff1591a90481)















![{\displaystyle \mathbf {v^{1}} ={\frac {1}{\sqrt {N}}}[1,1,...,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e55a95330752e00904ca3160f9194a87ae62a522)

