Geodesic dome

Doubling the cube (also known as the Delian problem) is one of the three most famous geometric problems unsolvable by compass and straightedge construction. It was known to the Egyptians, Greeks, and Indians.

To "double the cube" means to be given a cube of some side length s and volume V= s³, and to construct the side of a new cube, larger than the first, with volume 2V and therefore side length $s\cdot {\sqrt[{3}]{2}}$. The problem is known to be impossible to solve with only compass and straightedge, because ${\sqrt[{3}]{2}}$ ≈ 1.25992105... is not a constructible number.

History

The problem owes its name to a story concerning the citizens of Delos, who consulted the oracle at Delphi in order to learn how to defeat a plague sent by Apollo. According to Plutarch it was the citizens of Delos who consulted the oracle at Delphi, seeking a solution for their internal political problems at the time, which had intensified relationships among the citizens. The oracle responded that they must double the size of the altar to Apollo, which was a regular cube. The answer seemed strange to the Delians and they consulted Plato, who was able to interpret the oracle as the mathematical problem of doubling the volume of a given cube, thus explaining the oracle as the advice of Apollo for the citizens of Delos to occupy themselves with the study of geometry and mathematics in order to calm down their passions.

According to Plutarch, Plato gave the problem to Eudoxus and Archytas and Menaechmus, who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry (Plut., Quaestiones convivales VIII.ii, 718ef). This may be why the problem is referred to in the 350s BC by the author of the pseudo-Platonic Sisyphus (388e) as still unsolved. However another version of the story says that all three found solutions but they were too abstract to be of practical valuePotter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park..

A significant development in finding a solution to the problem was the discovery by Hippocrates of Chios that it is equivalent to finding two mean proportionals between a line segment and another with twice the length. In modern notation, this means that given segments of lengths a and 2a, the duplication of the cube is equivalent to finding segments of lengths r and s so that

${\frac {a}{r}}={\frac {r}{s}}={\frac {s}{2a}}.\$

In turn, this means that

$r=a\cdot {\sqrt[{3}]{2}}$

But Pierre Wantzel proved in 1837 that the cube root of 2 is not constructible; that is, it cannot be constructed with straightedge and compass.

Solutions

Menaechmus' original solution involves the intersection of two conic curves. Other more complicated methods of doubling the cube involve the cissoid of Diocles, the conchoid of Nicomedes, or the Philo line. Archytas solved the problem in the fourth century B.C. using geometric construction in three dimensions, determining a certain point as the intersection of three surfaces of revolution.

False claims of doubling the cube with compass and straightedge abound in mathematical crank literature (pseudomathematics).

Origami may also be used to construct the cube root of two by folding paper.

Using a marked ruler

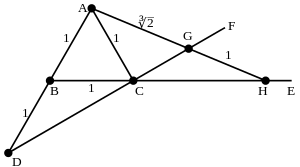
There is a simple neusis construction using a marked ruler for a length which is the cube root of 2 times another length.

• Mark a ruler with the given length, this will eventually be GH.
• Construct an equilateral triangle ABC with the given length as side.
• Extend AB an equal amount again to D.
• Extend the line BC forming the line CE.
• Extend the line DC forming the line CF
• Place the marked ruler so it goes through A and one end G of the marked length falls on CF and the other end of the marked length falls on ray CE. Thus GH is the given length.

The AG is the given length times the cube root of 2.

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

External links

• Other Sports Official Kull from Drumheller, has hobbies such as telescopes, property developers in singapore and crocheting. Identified some interesting places having spent 4 months at Saloum Delta.
  
  my web-site http://himerka.com/
• Doubling the cube. J. J. O'Connor and E. F. Robertson in the MacTutor History of Mathematics archive.
• To Double a Cube – The Solution of Archytas. Excerpted with permission from A History of Greek Mathematics by Sir Thomas Heath.
• Delian Problem Solved. Or Is It? at cut-the-knot.