Boolean satisfiability problem: Difference between revisions
→Self-reducibility: - very small correction - spelling of "unsatisfiable" |
en>Jochen Burghardt undid edit made in good faith by 197.207.52.162; reason: stay consistent with the remark at the end of section "3-satisfiability": "Some authors restrict k-SAT to CNF formulas with exactly k literals. ..." |
||
| Line 1: | Line 1: | ||
{{Redirect|3SAT|the Central European television network|3sat}} | |||
In [[computer science]], '''Boolean''', or '''propositional''', '''satisfiability''' (often written '''SATISFIABILITY''' or abbreviated '''SAT''') is the problem of determining if there exists an [[Interpretation (logic)|interpretation]] that [[Satisfiability|satisfies]] a given [[Boolean logic|Boolean]] [[Formula (mathematical logic)|formula]]. In other words, it establishes if the variables of a given Boolean formula can be assigned in such a way as to make the formula [[Validity|evaluate to TRUE]]. If no such assignments exist, the function expressed by the formula is [[Contradiction#Contradiction_in_formal_logic|identically FALSE]] for all possible variable assignments. In this latter case, it is called '''unsatisfiable''', otherwise '''satisfiable'''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable. | |||
SAT was the first known example of an [[NP-complete]] problem. That briefly means that there is no known algorithm that efficiently solves all instances of SAT, and it is generally believed (but not proven, see [[P versus NP problem]]) that no such algorithm can exist. Further, a wide range of other naturally occurring decision and optimization problems can be transformed into instances of SAT. A class of algorithms called SAT solvers can efficiently solve a large enough subset of SAT instances to be useful in various practical areas such as [[circuit design]] and [[automatic theorem proving]], by solving SAT instances made by transforming problems that arise in those areas. Extending the capabilities of SAT solving algorithms is an ongoing area of research. However, no current such methods can efficiently solve ''all'' SAT instances. | |||
==Basic definitions and terminology== | |||
A '''[[propositional logic]] formula''', also called '''Boolean expression''', is built from [[Variable (mathematics)|variables]], operators AND ([[Logical conjunction|conjunction]], also denoted by ∧), OR ([[logical disjunction|disjunction]], ∨), NOT ([[negation]], ¬), and parentheses. | |||
A formula is said to be '''satisfiable''' if it can be made TRUE by assigning appropriate [[logical value]]s (i.e. TRUE, FALSE) to its variables. | |||
The '''Boolean satisfiability problem''' ('''SAT''') is, given a formula, to check whether it is satisfiable. | |||
This [[decision problem]] is of central importance in various areas of [[computer science]], including [[theoretical computer science]], [[computational complexity theory|complexity theory]], [[algorithmics]], and [[artificial intelligence]]. | |||
There are several special cases of the Boolean satisfiability problem in which the formulas are required to have a particular structure. | |||
A '''literal''' is either a variable, then called '''positive literal''', or the negation of a variable, then called '''negative literal'''. | |||
A '''clause''' is a disjunction of literals (or a single literal). | |||
A clause is called '''[[Horn clause]]''' if it contains at most one positive literal. | |||
A formula is in '''[[conjunctive normal form]]''' ('''CNF''') if it is a conjunction of clauses (or a single clause). | |||
For example, "''x''<sub>1</sub>" is a positive literal, "¬''x''<sub>2</sub>" is a negative literal, "''x''<sub>1</sub> ∨ ¬''x''<sub>2</sub>" is a clause, and "(''x''<sub>1</sub> ∨ ¬''x''<sub>2</sub>) ∧ (¬''x''<sub>1</sub> ∨ ''x''<sub>2</sub> ∨ ''x''<sub>3</sub>) ∧ ¬''x''<sub>1</sub>" is a formula in conjunctive normal form, its 1st and 3rd clause is a Horn clause, but its 2nd clause is not. The formula is satisfiable, choosing ''x''<sub>1</sub>=FALSE, ''x''<sub>2</sub>=FALSE, and ''x''<sub>3</sub> arbitrarily, since (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ ''x''<sub>3</sub>) ∧ ¬FALSE evaluates to (FALSE ∨ TRUE) ∧ (TRUE ∨ FALSE ∨ ''x''<sub>3</sub>) ∧ TRUE, and in turn to TRUE ∧ TRUE ∧ TRUE (i.e. to TRUE). In contrast, the CNF formula ''a'' ∧ ¬''a'', consisting of two clauses of one literal, is unsatisfiable, since for ''a''=TRUE and ''a''=FALSE it evaluates to TRUE ∧ ¬TRUE (i.e. to FALSE) and FALSE ∧ ¬FALSE (i.e. again to FALSE), respectively. | |||
For some versions of the SAT problem, | |||
<!---need not list them in detail here---(viz. [[#Exactly-1 3-satisfiability|Exactly-1 3-satisfiability]], [[#XOR-satisfiability|XOR-satisfiability]], and, more general, [[#Schaefer's dichotomy theorem|Schaefer's dichotomy theorem]], discussed below),---> | |||
it is useful to define the notion of a '''generalized conjunctive normal form''' formula, viz. as a conjunction of arbitrarily many '''generalized clauses''', the latter being of the form ''R''(''l''<sub>1</sub>,...,''l''<sub>''n''</sub>) for some boolean operator ''R'' and (ordinary) literals ''l''<sub>''i''</sub>. Different sets of allowed boolean operators lead to different problem versions. | |||
<!---, see [[#Complexity and restricted versions|below]].---> | |||
As an example, ''R''(¬''x'',''a'',''b'') is a generalized clause, and ''R''(¬''x'',''a'',''b'') ∧ ''R''(''b'',''y'',''c'') ∧ ''R''(''c'',''d'',¬''z'') is a generalized conjunctive normal form. This formula is used [[#Exactly-1 3-satisfiability|below]], with ''R'' being the ternary operator that is TRUE just if exactly one of its arguments is. | |||
<!---need not explain that alread yhere---If ''R'' is the ternary operator that is TRUE just if exactly one of its arguments is, then a satisfying assignment for the latter formula can be found starting from every possible combination of truth values for ''x'', ''y'', ''z'', except ''x''=''y''=''z''=FALSE, and choosing the values of ''a'', ''b'', ''c'', ''d'' appropriately; cf. the left table under [[#Exactly-1 3-satisfiability|Exactly-1 3-satisfiability]] below.---> | |||
Using the laws of [[Boolean algebra (structure)|Boolean algebra]], every propositional logic formula can be transformed into an equivalent conjunctive normal form, which may, however, be exponentially longer. For example, transforming the formula | |||
(''x''<sub>1</sub>∧''y''<sub>1</sub>) ∨ (''x''<sub>2</sub>∧''y''<sub>2</sub>) ∨ ... ∨ (''x''<sub>''n''</sub>∧''y''<sub>''n''</sub>) | |||
into conjunctive normal form yields | |||
(''x''<sub>1</sub>∨''x''<sub>2</sub>∨…∨''x''<sub>''n''</sub>) ∧ | |||
(''y''<sub>1</sub>∨''x''<sub>2</sub>∨…∨''x''<sub>''n''</sub>) ∧ | |||
(''x''<sub>1</sub>∨''y''<sub>2</sub>∨…∨''x''<sub>''n''</sub>) ∧ | |||
(''y''<sub>1</sub>∨''y''<sub>2</sub>∨…∨''x''<sub>''n''</sub>) ∧ ... ∧ | |||
(''x''<sub>1</sub>∨''x''<sub>2</sub>∨…∨''y''<sub>''n''</sub>) ∧ | |||
(''y''<sub>1</sub>∨''x''<sub>2</sub>∨…∨''y''<sub>''n''</sub>) ∧ | |||
(''x''<sub>1</sub>∨''y''<sub>2</sub>∨…∨''y''<sub>''n''</sub>) ∧ | |||
(''y''<sub>1</sub>∨''y''<sub>2</sub>∨…∨''y''<sub>''n''</sub>); | |||
while the former is a disjunction of ''n'' conjunctions of 2 variables, the latter consists of 2<sup>''n''</sup> clauses of ''n'' variables. | |||
==Complexity and restricted versions== | |||
===Unrestricted satisfiability (SAT)=== | |||
{{Main|Cook–Levin theorem}} | |||
SAT was the first known [[NP-complete]] problem, as proved by [[Stephen Cook]] in 1971<ref>{{cite book| author=Stephen A. Cook| chapter=The Complexity of Theorem-Proving Procedures| title=Proc. 3rd ann. Symp. on Theory of Computer| year=1971| pages=151–158| url=http://www.cs.toronto.edu/~sacook/homepage/1971.pdf| doi=10.1145/800157.805047}}</ref> and independently by [[Leonid Levin]] in 1973.<ref>{{cite journal|last=Levin|first=Leonid|authorlink=Leonid Levin|title = Universal search problems ({{lang-ru|Универсальные задачи перебора}}, Universal'nye perebornye zadachi)|journal = Problems of Information Transmission ({{lang-ru|Проблемы передачи информа́ции}}, Problemy Peredachi Informatsii)|volume = 9|issue = 3|pages = 115–116|year = 1973}} [http://www.mathnet.ru/php/getFT.phtml?jrnid=ppi&paperid=914&volume=9&year=1973&issue=3&fpage=115&what=fullt&option_lang=eng (pdf)] {{ru icon}}, translated into English by {{cite journal|last=Trakhtenbrot|first=B. A.|title = A survey of Russian approaches to ''perebor'' (brute-force searches) algorithms|journal = Annals of the History of Computing |volume = 6|issue = 4|pages = 384–400|year = 1984|doi=10.1109/MAHC.1984.10036}}</ref> Until that time, the concept of an NP-complete problem did not even exist. | |||
The proof shows how every decision problem in the [[complexity class]] [[NP (complexity)|NP]] can be [[reduction (complexity)|reduced]] to the SAT problem for CNF<ref group=note>The SAT problem for ''arbitrary'' formulas is NP-complete, too, since it is easily shown to be in NP, and it cannot be easier than SAT for CNF formulas.</ref> formulas. | |||
A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, deciding whether a given [[graph (mathematics)|graph]] has a [[Graph coloring#Vertex_coloring|3-coloring]] is another problem in NP; if a graph has 17 valid 3-colorings, the SAT formula produced by the Cook–Levin reduction will have 17 satisfying assignments. | |||
NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See [[#Algorithms for solving SAT|Algorithms for solving SAT]] below. | |||
SAT is trivial if the formulas are restricted to those in '''[[disjunctive normal form]]''', that is, they are disjunction of conjunctions of literals. Such a formula is indeed satisfiable if and only if at least one of its conjunctions is satisfiable, and a conjunction is satisfiable if and only if it does not contain both ''x'' and NOT ''x'' for some variable ''x''. This can be checked in linear time. Furthermore, if they are restricted to being in '''full disjunctive normal form''', in which every variable appears exactly once in every conjunction, they can be checked in constant time (each conjunction represents one satisfying assignment). But it can take exponential time and space to convert a general SAT problem to disjunctive normal form; for an example exchange "∧" and "∨" in the [[#Basic definitions and terminology|above]] exponential blow-up example for conjunctive normal forms. | |||
===3-satisfiability=== | |||
[[File:Sat reduced to Clique from Sipser.svg|thumb|The 3-SAT instance (''x''∨''x''∨''y'') ∧ (¬''x''∨¬''y''∨¬''y'') ∧ (¬''x''∨''y''∨''y'') reduced to a [[clique problem]]. The green vertices form a 3-clique and correspond to the satisfying assignment ''x''=FALSE, ''y''=TRUE.]] | |||
Like the satisfiability problem for arbitrary formulas, determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete also; this problem is called '''3-SAT''', '''3CNFSAT''', or '''3-satisfiability'''. | |||
To reduce the unrestricted SAT problem to 3-SAT, transform each clause "''l''<sub>1</sub> ∨ ... ∨ ''l''<sub>''n''</sub>" to a conjunction of ''n''-2 clauses | |||
"(''l''<sub>1</sub> ∨ ''l''<sub>2</sub> ∨ ''x''<sub>2</sub>) ∧ | |||
(¬''x''<sub>2</sub> ∨ ''l''<sub>3</sub> ∨ ''x''<sub>3</sub>) ∧ | |||
(¬''x''<sub>3</sub> ∨ ''l''<sub>4</sub> ∨ ''x''<sub>4</sub>) ∧ ... ∧ | |||
(¬''x''<sub>''n''-3</sub> ∨ ''l''<sub>''n''-2</sub> ∨ ''x''<sub>''n''-2</sub>) ∧ | |||
(¬''x''<sub>''n''-2</sub> ∨ ''l''<sub>''n''-1</sub> ∨ ''l''<sub>n</sub>)", where ''x''<sub>2</sub>,...,''x''<sub>''n''-2</sub> are fresh variables not occurring elsewhere. | |||
Although both formulas are not [[logically equivalent]], they are [[equisatisfiable]]. The formula resulting from transforming all clauses is at most 3 times as long as its original, i.e. the length growth is polynomial.<ref name="Aho.Hopcroft.Ullman.1974">{{cite book| author=Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullman| title=The Design and Analysis of Computer Algorithms| year=1974| publisher=Addison-Wesley}}; here: Thm.10.4</ref> | |||
3-SAT is one of [[Karp's 21 NP-complete problems]], and it is used as a starting point for proving that other problems are also [[NP-hard]].<ref group=note>i.e. at least as hard as every other problem in NP. A problem is NP-complete if and only if it is in NP and is NP-hard.</ref> This is done by [[polynomial-time reduction]] from 3-SAT to the other problem. An example of a problem where this method has been used is the [[clique problem]]: given a CNF formula consisting of ''c'' clauses, the corresponding [[Graph (mathematics)|graph]] consists of a vertex for each literal, and an edge between each two non-contradicting<ref group=note>i.e. such that one literal isn't the negation of the other</ref> literals from different clauses, cf. picture. The graph has a ''c''-clique if and only if the formula is satisfiable.{{refn|Aho, Hopcroft, Ullman<ref name="Aho.Hopcroft.Ullman.1974"/> (1974); Thm.10.5}} | |||
There is a simple randomized algorithm due to Schöning (1999) that runs in time (4/3)<sup>''n''</sup> where ''n'' is the number of clauses and succeeds with high probability to correctly decide 3-SAT.<ref name="Schoning.1999">{{cite book| author=Uwe Schöning| chapter=A Probabilistic Algorithm for $k$-SAT and Constraint Satisfaction Problems| title=Proc. 40th Ann. Symp. Foundations of Computer Science|date=Oct 1999| pages=410-414| url=http://homepages.cwi.nl/~rdewolf/schoning99.pdf| doi=10.1109/SFFCS.1999.814612}}</ref> | |||
The [[exponential time hypothesis]] is that no algorithm can solve 3-SAT faster than [[Small o notation#Little-o notation|''o'']](''exp''(''n'')). | |||
Selman, Mitchell, and Levesque (1996) give empirical data on the difficulty of randomly generated 3-SAT formulas, depending on their size parameters. | |||
Difficuly is measured in number recursive calls made by a [[#Algorithms for solving SAT|DPLL algorithm]].<ref>{{cite journal| author=Bart Selman, David Mitchell, Hector Levesque| title=Generating Hard Satisfiability Problems| journal=Artificial Intelligence| year=1996| volume=81| pages=17–29| url=http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=3CBEAB7E11BF4B2283E9F383810060C1?doi=10.1.1.37.7362&rep=rep1&type=pdf}}</ref> | |||
3-satisfiability can be generalized to '''k-satisfiability''' ('''k-SAT'''), when formulas in CNF are considered with each clause containing up to ''k'' literals. | |||
However, since for any ''k''≥3, this problem can neither be easier than 3-SAT nor harder than SAT, and the latter two are NP-complete, so must be k-SAT. | |||
Some authors restrict k-SAT to CNF formulas with '''exactly k literals'''. This doesn't lead to a different complexity class either, as each clause "''l''<sub>1</sub> ∨ ... ∨ ''l''<sub>''j''</sub>" with ''j''<''k'' literals can be padded with fixed dummy variables to | |||
"''l''<sub>1</sub> ∨ ... ∨ ''l''<sub>''j''</sub> ∨ ''d''<sub>''j''+1</sub> ∨ ... ∨ ''d''<sub>''k''</sub>". | |||
After padding all clauses, 2<sup>''k''</sup>-1 extra clauses<ref group=note>viz. all [[Canonical_form_(Boolean_algebra)#Maxterms|maxterms]] that can be built with ''d''<sub>1</sub>,...,''d''<sub>''k''</sub>, except "''d''<sub>1</sub>∨...∨''d''<sub>''k''</sub>"</ref> have to be appended to ensure that only ''d''<sub>1</sub>=...=''d''<sub>k</sub>=FALSE can lead to a satisfying assignment. Since ''k'' doesn't depend on the formula length, the extra clauses lead to a constant increase in length. For the same reason, it does not matter whether '''duplicate literals''' are allowed in clauses (like e.g. "¬''x'' ∨ ¬''y'' ∨ ¬''y''"), or not. | |||
===Exactly-1 3-satisfiability=== | |||
[[File:Schaefer's 3-SAT to 1-in-3-SAT reduction.gif|thumb|x100px|'''Left:''' Schaefer's reduction of a 3-SAT clause ''x''∨''y''∨''z''. The result of ''R'' is {{fontcolor|#00a000|TRUE (1)}} if exactly one of its arguments is TRUE, and {{fontcolor|#a00000|FALSE (0)}} otherwise. All 8 combinations of values for ''x'',''y'',''z'' are examined, one per line. The fresh variables ''a'',...,''f'' can be chosen to satisfy all clauses (exactly one {{fontcolor|#00a000|green}} argument for each ''R'') in all lines except the first, where ''x''∨''y''∨''z'' is FALSE. '''Right:''' A simpler reduction with the same properties.]] | |||
A variant of the 3-satisfiability problem is the '''one-in-three 3-SAT''' (also known variously as '''1-in-3-SAT''' and '''exactly-1 3-SAT'''). | |||
Given a conjunctive normal form, the problem is to determine whether there exists a truth assignment to the variables so that each clause has ''exactly'' one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has ''at least'' one TRUE literal. | |||
Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator ''R'' that is TRUE just if exactly one of its arguments is. | |||
One-in-three 3-SAT is listed as NP-complete problem "LO4" in the standard reference, ''Computers and Intractability: A Guide to the Theory of NP-Completeness'' | |||
by [[Michael R. Garey]] and [[David S. Johnson]]. It was proved to be NP-complete by [[Thomas J. Schaefer]] as a special case of [[Schaefer's dichotomy theorem]], which asserts that any problem generalizing Boolean satisfiability in a certain way is either in the class P or is NP-complete.<ref name="schaefer"> | |||
{{cite conference | |||
| last = Schaefer | |||
| first = Thomas J. | |||
| title = The complexity of satisfiability problems | |||
| booktitle = Proceedings of the 10th Annual ACM Symposium on Theory of Computing | |||
| place = San Diego, California | |||
| pages = 216–226 | |||
| year = 1978 | |||
| url = http://www.ccs.neu.edu/home/lieber/courses/csg260/f06/materials/papers/max-sat/p216-schaefer.pdf | |||
| doi = 10.1145/800133.804350 | |||
}}</ref> | |||
Schaefer gives a construction allowing an easy polynomial-time reduction from 3-SAT to one-in-three 3-SAT. Let "(''x'' or ''y'' or ''z'')" be a clause in a 3CNF formula. Add six fresh boolean variables ''a'', ''b'', ''c'', ''d'', ''e'', and ''f'', to be used to simulate this clause and no other. | |||
<!---now introduced already above---Let ''R''(''u'',''v'',''w'') be a predicate that is TRUE if and only if exactly one of the booleans ''u'', ''v'', and ''w'' | |||
is TRUE.---> | |||
Then the formula ''R''(''x'',''a'',''d'') ∧ ''R''(''y'',''b'',''d'') ∧ ''R''(''a'',''b'',''e'') ∧ ''R''(''c'',''d'',''f'') ∧ ''R''(''z'',''c'',FALSE) is satisfiable by some setting of the fresh variables if and only if at least one of ''x'', ''y'', or ''z'' is TRUE, see picture (left). Thus any 3-SAT instance with ''m'' clauses and ''n'' variables may be converted into an [[equisatisfiable]] one-in-three 3-SAT instance with 5''m'' clauses and ''n''+6''m'' variables.<ref>(Schaefer, 1978), p.222, Lemma 3.5</ref> | |||
Another reduction involves only four fresh variables and three clauses: ''R''(¬''x'',''a'',''b'') ∧ ''R''(''b'',''y'',''c'') ∧ R(''c'',''d'',¬''z''), see picture (right). | |||
The one-in-three 3-SAT problem is often used in the literature as a known NP-complete problem in a reduction to show that other problems are NP-complete.{{citation needed|date=September 2013}} | |||
===2-satisfiability=== | |||
{{Main|2-satisfiability}} | |||
SAT is easier if the number of literals in a clause is limited to at most 2, in which case the problem is called '''[[2-SAT]]'''. This problem can be solved in polynomial time, and in fact is [[NL-complete|complete]] for the complexity class [[NL (complexity)|NL]]. If additionally all OR operations in literals are changed to [[Exclusive or|XOR]] operations, the result is called '''exclusive-or 2-satisfiability''', which is a problem complete for the complexity class [[SL (complexity)|SL]] = [[L (complexity)|L]]. | |||
===Horn-satisfiability=== | |||
{{Main|Horn-satisfiability}} | |||
The problem of deciding the satisfiability of a given conjunction of Horn clauses is called '''Horn-satisfiability''', or '''HORN-SAT'''. | |||
It can be solved in polynomial time by a single step of the [[Unit propagation]] algorithm, which produces the single minimal model of the set of Horn clauses (w.r.t. the set of literals assigned to TRUE). | |||
Horn-satisfiability is [[P-complete]]. It can be seen as [[P (complexity)|P's]] version of the Boolean satisfiability problem. | |||
Horn clauses are of interest because they are able to express [[Entailment|implication]] of one variable from a set of other variables. Indeed, one such clause ¬''x''<sub>1</sub> ∨ ... ∨ ¬''x''<sub>''n''</sub> ∨ ''y'' can be rewritten as ''x''<sub>1</sub> ∧ ... ∧ ''x''<sub>''n''</sub> → ''y'', that is, if ''x''<sub>1</sub>,...,''x''<sub>''n''</sub> are all TRUE, then ''y'' needs to be TRUE as well. | |||
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. | |||
For example, (''x''<sub>1</sub> ∨ ¬''x''<sub>2</sub>) ∧ (¬''x''<sub>1</sub> ∨ ''x''<sub>2</sub> ∨ ''x''<sub>3</sub>) ∧ ¬''x''<sub>1</sub> is not a Horn formula, but can be renamed to the Horn formula (''x''<sub>1</sub> ∨ ¬''x''<sub>2</sub>) ∧ (¬''x''<sub>1</sub> ∨ ''x''<sub>2</sub> ∨ ¬''y''<sub>3</sub>) ∧ ¬''x''<sub>1</sub> by introducing ''y''<sub>3</sub> as negation of ''x''<sub>3</sub>. | |||
In contrast, no renaming of (''x''<sub>1</sub> ∨ ¬''x''<sub>2</sub> ∨ ¬''x''<sub>3</sub>) ∧ (¬''x''<sub>1</sub> ∨ ''x''<sub>2</sub> ∨ ''x''<sub>3</sub>) ∧ ¬''x''<sub>1</sub> leads to a Horn formula. | |||
Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula. | |||
{| style="float:right" | |||
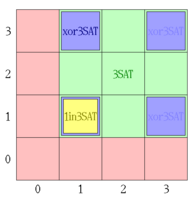
| [[File:Boolean satisfiability vs true literal counts.gif|thumb|x200px|A formula with 2 clauses may be unsatisfied (red), 3-satisfied (green), xor-3-satisfied (blue), or/and 1-in-3-satisfied (yellow), depending on the TRUE-literal count in the 1st (hor) and 2nd (vert) clause.]] | |||
|} | |||
===XOR-satisfiability=== | |||
{| align="right" class="wikitable collapsible collapsed" style="text-align:left" | |||
|- | |||
! Solving an XOR-SAT example<BR>by [[Gaussian elimination]] | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! Given formula | |||
|- | |||
| ("⊕" means XOR, the {{color|#ff8080|red clause}} is optional) | |||
|- | |||
| (''a''⊕''c''⊕''d'') ∧ (''b''⊕¬''c''⊕''d'') ∧ (''a''⊕''b''⊕¬''d'') ∧ (''a''⊕¬''b''⊕¬''c'') {{color|#ff8080|∧ (¬''a''⊕''b''⊕''c'')}} | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! colspan="9" | Equation system | |||
|- | |||
| colspan="9" | ("1" means TRUE, "0" means FALSE) | |||
|- | |||
| colspan="9" | Each clause leads to one equation. | |||
|- | |||
| || ''a'' || ⊕ || || ''c'' || ⊕ || || ''d'' || = 1 | |||
|- | |||
| || ''b'' || ⊕ || ¬ || ''c'' || ⊕ || || ''d'' || = 1 | |||
|- | |||
| || ''a'' || ⊕ || || ''b'' || ⊕ || ¬ || ''d'' || = 1 | |||
|- | |||
| || ''a'' || ⊕ || ¬ || ''b'' || ⊕ || ¬ || ''c'' || = 1 | |||
|- | |||
| {{color|#ff8080|¬}} || {{color|#ff8080|''a''}} || {{color|#ff8080|⊕}} || || {{color|#ff8080|''b''}} || {{color|#ff8080|⊕}} || || {{color|#ff8080|''c''}} || {{color|#ff8080| ≃ 1}} | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! colspan="6" | Normalized equation system | |||
|- | |||
| colspan="6" | using properties of [[Boolean rings]] (¬''x''=1⊕''x'', ''x''⊕''x''=0) | |||
|- | |||
| ''a'' || ⊕ || ''c'' || ⊕ || ''d'' || = '''1''' | |||
|- | |||
| ''b'' || ⊕ || ''c'' || ⊕ || ''d'' || = '''0''' | |||
|- | |||
| ''a'' || ⊕ || ''b'' || ⊕ || ''d'' || = '''0''' | |||
|- | |||
| ''a'' || ⊕ || ''b'' || ⊕ || ''c'' || = '''1''' | |||
|- | |||
| {{color|#ff8080|''a''}} || {{color|#ff8080|⊕}} || {{color|#ff8080|''b''}} || {{color|#ff8080|⊕}} || {{color|#ff8080|''c''}} || {{color|#ff8080| ≃ '''0'''}} | |||
|- | |||
| colspan="6" | (If the {{color|#ff8080|red equation}} is present, {{color|#ff8080|it}} contradicts | |||
|- | |||
| colspan="6" | the last black one, so the system is unsolvable. | |||
|- | |||
| colspan="6" | Therefore, Gauss' algorithm is | |||
|- | |||
| colspan="6" | used only for the black equations.) | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! colspan="6" | Associated coefficient matrix | |||
|- | |||
| | |||
|- | |||
! ''a'' !! ''b'' !! ''c'' !! ''d'' !! !! line | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 1 || 1 | |||
! 1 | |||
| A | |||
|- | |||
| 0 || 1 || 1 || 1 | |||
! 0 | |||
| B | |||
|- | |||
| 1 || 1 || 0 || 1 | |||
! 0 | |||
| C | |||
|- | |||
| 1 || 1 || 1 || 0 | |||
! 1 | |||
| D | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! colspan="6" |Transforming to echelon form | |||
|- | |||
| | |||
|- | |||
! ''a'' !! ''b'' !! ''c'' !! ''d'' !! !! operation | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 1 || 1 | |||
! 1 | |||
| A | |||
|- | |||
| 1 || 1 || 0 || 1 | |||
! 0 | |||
| C | |||
|- | |||
| 1 || 1 || 1 || 0 | |||
! 1 | |||
| D | |||
|- | |||
| 0 || 1 || 1 || 1 | |||
! 0 | |||
| B (swapped) | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 1 || 1 | |||
! 1 | |||
| A | |||
|- | |||
| 0 || 1 || 1 || 0 | |||
! 1 | |||
| E = C⊕A | |||
|- | |||
| 0 || 1 || 0 || 1 | |||
! 0 | |||
| F = D⊕A | |||
|- | |||
| 0 || 1 || 1 || 1 | |||
! 0 | |||
| B | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 1 || 1 | |||
! 1 | |||
| A | |||
|- | |||
| 0 || 1 || 1 || 0 | |||
! 1 | |||
| E | |||
|- | |||
| 0 || 0 || 1 || 1 | |||
! 1 | |||
| G = F⊕E | |||
|- | |||
| 0 || 0 || 0 || 1 | |||
! 1 | |||
| H = B⊕E | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! colspan="6" | Transforming to diagonal form | |||
|- | |||
| | |||
|- | |||
! ''a'' !! ''b'' !! ''c'' !! ''d'' !! !! operation | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 1 || 0 | |||
! 0 | |||
| I = A⊕H | |||
|- | |||
| 0 || 1 || 1 || 0 | |||
! 1 | |||
| E | |||
|- | |||
| 0 || 0 || 1 || 0 | |||
! 0 | |||
| J = G⊕H | |||
|- | |||
| 0 || 0 || 0 || 1 | |||
! 1 | |||
| H | |||
|- | |||
| | |||
|- | |||
| 1 || 0 || 0 || 0 | |||
! 0 | |||
| K = I⊕J | |||
|- | |||
| 0 || 1 || 0 || 0 | |||
! 1 | |||
| L = E⊕J | |||
|- | |||
| 0 || 0 || 1 || 0 | |||
! 0 | |||
| J | |||
|- | |||
| 0 || 0 || 0 || 1 | |||
! 1 | |||
| H | |||
|- | |||
|} | |||
|- | |||
| | |||
{| align="left" class="collapsible collapsed" style="text-align:left" | |||
|- | |||
! Solution: | |||
|- | |||
| If the {{color|#ff8080|red clause}} is present: || Unsolvable | |||
|- | |||
| Else: || ''a'' = 0 = FALSE | |||
|- | |||
| || ''b'' = 1 = TRUE | |||
|- | |||
| || ''c'' = 0 = FALSE | |||
|- | |||
| || ''d'' = 1 = TRUE | |||
|- | |||
| colspan="2" | '''As a consequence:''' | |||
|- | |||
| colspan="2" | ''R''(''a'',''c'',''d'') ∧ ''R''(''b'',¬''c'',''d'') ∧ ''R''(''a'',''b'',¬''d'') ∧ ''R''(''a'',¬''b'',¬''c'') {{color|#ff8080|∧ ''R''(¬''a'',''b'',''c'')}} | |||
|- | |||
| colspan="2" | is not 1-in-3-satisfiable, | |||
|- | |||
| colspan="2" | while (''a''∨''c''∨''d'') ∧ (''b''∨¬''c''∨''d'') ∧ (''a''∨''b''∨¬''d'') ∧ (''a''∨¬''b''∨¬''c'') | |||
|- | |||
| colspan="2" | is 3-satisfiable with ''a''=''c''=FALSE and ''b''=''d''=TRUE. | |||
|} | |||
|} | |||
Another special case is the class of problems where each clause contains XOR (i.e. [[exclusive or]]) rather than (plain) OR operators.<ref group=note>Formally, generalized conjunctive normal forms with a ternary boolean operator ''R'' are employed, which is TRUE just if 1 or 3 of its arguments is. An input clause with more than 3 literals can be transformed into an equisatisfiable conjunction of clauses á 3 literals similar to [[#3-satisfiability|above]]; i.e. XOR-SAT can be reduced to XOR-3-SAT.</ref> | |||
This is in [[P (complexity class)|P]], since an XOR-SAT formula can also be viewed as a system of linear equations mod 2, and can be solved in cubic time by [[Gaussian elimination]], see box for an example.{{citation needed|reason=Although the example computation seems to be ok, it is not immediately obvious why Gauss' algorithm is applicable and its solution(s) are solutions of XOR-SAT. In particular, the algorithm needs a field, not a ring, and its solutions need not be in {0,1} in general.|date=September 2013}} This recast is based on the [[Boolean_algebra_(structure)#Boolean_rings|kinship between Boolean algebras and Boolean rings]]. Since ''a'' XOR ''b'' XOR ''c'' evaluates to TRUE if and only if exactly 1 or 3 members of {''a'',''b'',''c''} are TRUE, each solution of the 1-in-3-SAT problem for a given CNF formula is also a solution of the XOR-3-SAT problem, and in turn each solution of XOR-3-SAT is a solution of 3-SAT, cf. picture. As a consequence, for each CNF formula, either the 3-SAT problem or the 1-in-3-SAT problem can be decided in cubic time to be solvable or unsolvable, respectively.{{clarify|reason=This consequence seems strange, but valid. Somebody please crosscheck.|date=September 2013}} | |||
Provided that the [[P = NP problem|complexity classes P and NP are not equal]], neither 2-, nor Horn-, nor XOR-satisfiability is NP-complete, unlike SAT. The assumption that P and NP are not equal is [[Unsolved problems of mathematics#Millennium Prize Problems|currently not proven]]. | |||
===Schaefer's dichotomy theorem=== | |||
{{Main|Schaefer's dichotomy theorem}} | |||
The restrictions above (CNF, 2CNF, 3CNF, Horn, XOR-SAT) bound the considered formulae to be conjunction of subformulae; each restriction states a specific form for all subformulae: for example, only binary clauses can be subformulae in 2CNF. | |||
Schaefer's dichotomy theorem states that, for any restriction to Boolean operators that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF, Horn, and XOR-SAT formulae are special cases of this theorem. | |||
==Extensions of SAT== | |||
An extension that has gained significant popularity since 2003 is '''[[Satisfiability modulo theories]]''' ('''SMT''') that can enrich CNF formulas with linear constraints, arrays, all-different constraints, [[uninterpreted function]]s,<ref name="Bryant.German.Velev.1999">R. E. Bryant, S. M. German, and M. N. Velev, [http://portal.acm.org/citation.cfm?id=709275 Microprocessor Verification Using Efficient Decision Procedures for a Logic of Equality with Uninterpreted Functions], in Analytic Tableaux and Related Methods, pp. 1–13, 1999.</ref> ''etc.'' Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints. | |||
The satisfiability problem becomes more difficult if both "for all" (∀) and "there exists" (∃) [[quantifier]]s are allowed to bind the Boolean variables. | |||
An example of such an expression would be "∀''x'' ∀''y'' ∃''z'' (''x'' ∨ ''y'' ∨ ''z'') ∧ (¬''x'' ∨ ¬''y'' ∨ ¬''z'')"; it is valid, since for all values of ''x'' and ''y'', an appropriate value of ''z'' can be found, viz. ''z''=TRUE if both ''x'' and ''y'' are FALSE, and ''z''=FALSE else. | |||
SAT itself (tacitly) uses only ∃ quantifiers. | |||
If only ∀ quantifiers are allowed instead, the so-called '''[[Tautology (logic)|tautology]] problem''' is obtained, which is [[Co-NP-complete]]. | |||
If both quantifiers are allowed, the problem is called the '''[[quantified Boolean formula problem]]''' ('''QBF'''), which can be shown to be [[PSPACE-complete]]. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved. | |||
A number of variants deal with the number of variable assignments making the formula TRUE. Ordinary SAT asks if there is at least one such assignment. '''MAJ-SAT''', which asks if the majority of all assignments make the formula TRUE, is complete for [[PP (complexity)|PP]], a probabilistic class. The problem of '''how many variable assignments''' satisfy a formula, not a decision problem, is in [[Sharp-P|#P]]. '''UNIQUE-SAT''' is the problem of determining whether a formula has exactly one assignment, it is complete for [[US (complexity)|US]].{{clarify|reason=As long as there is no article available, the complexity class 'US' should be defined here explicitly.|date=September 2013}} When the input is [[Promise problem|restricted]] to formulas having at most one satisfying assignment (or none), the problem is called '''UNAMBIGOUS-SAT'''. A solving algorithm for UNAMBIGOUS-SAT is allowed to exhibit any behavior, including endless looping, on a formula having several satisfying assignments. Although this problem seems easier, Valiant and Vazirani have [[Valiant-Vazirani theorem|shown]]<ref>{{cite doi|10.1016/0304-3975(86)90135-0}}</ref> that if there is a practical (i.e. [[Bounded-error probabilistic polynomial|randomized polynomial-time]]) algorithm to solve it, then all problems in [[NP (complexity class)|NP]] can be solved just as easily. | |||
The '''[[maximum satisfiability problem]]''', an [[FNP (complexity)|FNP]] generalization of SAT, asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient [[approximation algorithm]]s, but is NP-hard to solve exactly. Worse still, it is [[APX]]-complete, meaning there is no [[polynomial-time approximation scheme]] (PTAS) for this problem unless P=NP. | |||
Other generalisations include satisfiability for [[first-order predicate calculus|first]]- and [[second-order logic]], [[constraint satisfaction problem]]s, [[0-1 integer programming]]. | |||
==Self-reducibility== | |||
The SAT problem is '''self-reducible''', that is, each algorithm which correctly answers if an instance of SAT is solvable can be used to find a satisfying assignment. First, the question is asked on the given formula Φ. If the answer is "no", the formula is unsatisfiable. Otherwise, the question is asked on the partly instantiated formula Φ[[substitution (logic)|{''x''<sub>1</sub>=TRUE}]], i.e. Φ with the first variable ''x''<sub>1</sub> replaced by TRUE, and simplified accordingly. If the answer is "yes", then ''x''<sub>1</sub>=TRUE, otherwise ''x''<sub>1</sub>=FALSE. Values of other variables can be found subsequently in the same way. In total, ''n''+1 runs of the algorithm are required, where ''n'' is the number of distinct variables in Φ. | |||
This property of self-reducibility is used in several theorems in complexity theory: | |||
: [[NP (complexity)|NP]] ⊆ [[P/poly]] ⇒ [[PH (complexity)|PH]] = [[Polynomial_hierarchy#Definitions|Σ<sub>2</sub>]] ([[Karp–Lipton theorem]]){{clarify|reason=When adding the link for Σ2, I guessed from the 'Karp–Lipton theorem' article that the 'Polynomial hierarchy', rather than e.g. the 'Arithmetical hierarchy' was meant. This should be crosschecked by a complexity theory expert.|date=September 2013}} | |||
: [[NP (complexity)|NP]] ⊆ [[BPP (complexity)|BPP]] ⇒ [[NP (complexity)|NP]] = [[RP (complexity)|RP]] | |||
: [[P (complexity)|P]] = [[NP (complexity)|NP]] ⇒ [[FP (complexity)|FP]] = [[FNP (complexity)|FNP]] | |||
==Algorithms for solving SAT== | |||
Since the SAT problem is NP-complete, only algorithms with exponential worst-case complexity are known for it. In spite of this state of the art in complexity theory, efficient and scalable algorithms for SAT were developed over the last decade and have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints (i.e. clauses).{{citation needed|reason=Until 2013-09-16, this article claimed, without giving a particular source, both 'tens of thousands of variables and millions of constraints' (provisionally kept) and 'thousands of variables and tens of thousands of constraints' (removed). A source for one or the other version (or even for both) should be named.|date=September 2013}} Examples of such problems in [[electronic design automation]] (EDA) include [[formal equivalence checking]], [[model checking]], [[formal verification]] of [[microprocessor|pipelined microprocessors]],<ref name="Bryant.German.Velev.1999"/> [[automatic test pattern generation]], [[routing (electronic design automation)|routing]] of [[FPGA]]s,<ref>{{cite doi|10.1109/TCAD.2002.1004311}}</ref> [[Automated planning and scheduling|planning]], and [[Scheduling algorithm|scheduling problems]], and so on. A SAT-solving engine is now considered to be an essential component in the [[electronic design automation|EDA]] toolbox. | |||
There are two classes of high-performance [[algorithms]] for solving instances of SAT in practice: the [[conflict-driven clause learning]] algorithm, which can be viewed as a modern variant of the [[DPLL algorithm]] (well known implementation include [[Chaff algorithm|Chaff]],<ref>{{cite doi|10.1145/378239.379017}}</ref> [[GRASP (SAT solver)|GRASP]])<ref>{{cite doi|10.1109/12.769433}}</ref> and [[stochastic local search algorithm|stochastic]] [[Local search (constraint satisfaction)|local search]] algorithms, such as [[WalkSAT]]. | |||
A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 60s (see references below) and is now commonly referred to as the [[Davis–Putnam–Logemann–Loveland algorithm]] ("DPLL" or "DLL").<ref>{{cite doi|10.1145/321033.321034}}</ref><ref>{{cite doi|10.1145/368273.368557}}</ref> Theoretically, exponential lower bounds have been proved for the DPLL family of algorithms. | |||
In contrast, randomized algorithms like the PPSZ algorithm by Paturi, Pudlak, Saks, and Zane set variables in a random order according to some heuristics, for example bounded-width [[Resolution (logic)|resolution]]. If the heuristic can't find the correct setting, the variable is assigned randomly. The PPSZ algorithm has a runtime of <math>O(2^{0.386n})</math> for 3-SAT with a single satisfying assignment. Currently this is the best known runtime for this problem. In the setting with many satisfying assignments the randomized algorithm by Schöning has a better bound.<ref name="Schoning.1999"/><ref name="ppsz_algorithm">[http://dl.acm.org/citation.cfm?id=1066101 "An improved exponential-time algorithm for k-SAT"], Paturi, Pudlak, Saks, Zani</ref> | |||
Modern SAT solvers (developed in the last ten years) come in two flavors: "conflict-driven" and "look-ahead".{{clarify|reason=3 paragraphs before here, 'two classes', viz. 'conflict-driven clause learning DPLL' and 'stochastic local search' were named. Please indicate if the latter essentially means the same as 'look-ahead' here.|date=September 2013}} Conflict-driven solvers augment the basic DPLL search algorithm with efficient conflict analysis, clause learning, non-[[chronological backtracking]] (aka [[backjumping]]), as well as "two-watched-literals" unit propagation, adaptive branching, and random restarts. These "extras" to the basic systematic search have been empirically shown to be essential for handling the large SAT instances that arise in [[electronic design automation]] (EDA). Look-ahead solvers have especially strengthened reductions (going beyond unit-clause propagation) and the heuristics, and they are generally stronger than conflict-driven solvers on hard instances (while conflict-driven solvers can be much better on large instances which actually have an easy instance inside). | |||
Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others. Powerful solvers are readily available as [[free and open source software]]. In particular, the conflict-driven [http://minisat.se/ MiniSAT], which was relatively successful at the [http://www.satcompetition.org/ 2005 SAT competition], only has about 600 lines of code. A modern Parallel SAT solver is [http://www.cril.univ-artois.fr/~jabbour/manysat.htm ManySAT]. It can achieve super linear speed-ups on important classes of problems. An example for look-ahead solvers is [http://www.st.ewi.tudelft.nl/sat/march_dl.php march_dl], which won a prize at the [http://www.satcompetition.org/ 2007 SAT competition]. | |||
Certain types of large random satisfiable instances of SAT can be solved by [[survey propagation]] (SP). Particularly in [[hardware design]] and [[hardware verification|verification]] applications, satisfiability and other logical properties of a given propositional formula are sometimes decided based on a representation of the formula as a [[binary decision diagram]] (BDD). | |||
Almost all SAT solvers include time-outs, so they will terminate in reasonable time even if they cannot find a solution. | |||
Different SAT solvers will find different instances easy or hard, and some excel at proving unsatisfiability, and others at finding solutions. | |||
All of these behaviors can be seen in the SAT solving contests.<ref>{{cite web|url=http://www.satcompetition.org/ |title=The international SAT Competitions web page|accessdate=2007-11-15}}</ref> | |||
==See also== | |||
*[[Unsatisfiable core]] | |||
*[[Satisfiability Modulo Theories]] | |||
*[[Sharp-SAT|Counting SAT]] | |||
*[[Karloff–Zwick algorithm]] | |||
==Notes== | |||
{{reflist|group=note}} | |||
==References== | |||
{{reflist}} | |||
References are ordered by date of publication: | |||
{{refbegin|colwidth=25em}} | |||
* {{cite book|author = [[Michael R. Garey]] and [[David S. Johnson]] | year = 1979 | title = [[List of important publications in computer science#Computers and Intractability: A Guide to the Theory of NP-Completeness|Computers and Intractability: A Guide to the Theory of NP-Completeness]] | publisher = W.H. Freeman | isbn = 0-7167-1045-5}} A9.1: LO1 – LO7, pp. 259 – 260. | |||
* {{cite doi|10.1109/DATE.1999.761110}} | |||
* {{cite doi|10.1023/A:1011276507260}} | |||
* {{cite doi|10.1007/b95238}} | |||
* {{cite doi|10.1109/TC.2006.175}} | |||
* {{cite doi|10.1109/BIMNICS.2007.4610083}} | |||
* {{cite book|editor=Frank Van Harmelen, Vladimir Lifschitz, Bruce Porter|title=Handbook of knowledge representation|year=2008|publisher=Elsevier|isbn=978-0-444-52211-5|pages=89–134|author=Carla P. Gomes, Henry Kautz, Ashish Sabharwal, Bart Selman|chapter=Satisfiability Solvers|doi=10.1016/S1574-6526(07)03002-7|series=Foundations of Artificial Intelligence|volume=3}} | |||
{{refend|colwidth=25em}} | |||
== See also == | |||
* [[Circuit satisfiability]] | |||
==External links== | |||
=== SAT problem format === | |||
A SAT problem is often described in the [http://www.domagoj-babic.com/uploads/ResearchProjects/Spear/dimacs-cnf.pdf DIMACS-CNF] format: an input file in which each line represents a single disjunction. For example, a file with the two lines | |||
1 -5 4 0 | |||
-1 5 3 4 0 | |||
represents the formula "(''x''<sub>1</sub> ∨ ¬''x''<sub>5</sub> ∨ ''x''<sub>4</sub>) ∧ (¬''x''<sub>1</sub> ∨ ''x''<sub>5</sub> ∨ ''x''<sub>3</sub> ∨ ''x''<sub>4</sub>)". | |||
Another common format for this formula is the 7-bit [[ASCII]] representation "(x1 | ~x5 | x4) & (~x1 | x5 | x3 | x4)". | |||
[http://users.ics.aalto.fi/tjunttil/bcsat/ BCSAT] is a tool that converts input files in human-readable format to the DIMACS-CNF format. | |||
=== Online SAT solvers === | |||
* [http://www.boolsat.com BoolSAT] – Solves formulas in the DIMACS-CNF format or in a more human-friendly format: "a and not b or a". Runs on a server. | |||
* [http://www.msoos.org/2013/09/minisat-in-your-browser/ minisat-in-your-browser] – Solves formulas in the DIMACS-CNF format. Runs on the browser. | |||
=== Offline SAT solvers === | |||
* [http://minisat.se/ MiniSAT] – DIMACS-CNF format. | |||
* [http://fmv.jku.at/lingeling/ Lingeling] – won a gold medal in a 2011 SAT competition. | |||
** [http://fmv.jku.at/picosat/ PicoSAT] – an earlier solver from the Lingeling group. | |||
* [http://www.sat4j.org/ Sat4j] – DIMACS-CNF format. Java source code available. | |||
* [http://www.labri.fr/~lsimon/glucose Glucose] – DIMACS-CNF format. | |||
* [http://reasoning.cs.ucla.edu/rsat/home.html RSat] – won a gold medal in a 2007 SAT competition. | |||
* [http://ubcsat.dtompkins.com/ UBCSAT]. Supports unweighted and weighted clauses, both in the DIMACS-CNF format. C source code hosted on [https://github.com/dtompkins/ubcsat GitHub]. | |||
* [http://www.msoos.org/cryptominisat2 CryptoMiniSat] – won a gold medal in a 2011 SAT competition. C++ source code hosted on [https://github.com/msoos/cryptominisat GitHub]. Tries to put many useful features of MiniSat 2.0 core, PrecoSat ver 236, and Glucose into one package, adding many new features | |||
* [http://www.domagoj-babic.com/index.php/ResearchProjects/Spear Spear] – Supports bit-vector arithmetic. Can use the DIMACS-CNF format or the [http://www.domagoj-babic.com/uploads/ResearchProjects/Spear/spear-format.pdf Spear format]. | |||
** [http://www.domagoj-babic.com/index.php/ResearchProjects/HyperSAT HyperSAT] – Written to experiment with B-cubing search space pruning. Won 3rd place in a 2005 SAT competition. An earlier and slower solver from the developers of Spear. | |||
* [http://logic.pdmi.ras.ru/~basolver/ BASolver] | |||
* [http://argo.matf.bg.ac.rs/?content=downloads ArgoSAT] | |||
* [http://dudka.cz/fss Fast SAT Solver] – based on [[genetic algorithm]]s. | |||
* [http://www.princeton.edu/~chaff/zchaff.html zChaff] – not supported anymore. | |||
* [http://users.ics.aalto.fi/tjunttil/bcsat/ BCSAT] – human-readable boolean circuit format (also converts this format to the DIMACS-CNF format and automatically links to MiniSAT or zChaff). | |||
=== SAT applications === | |||
* [http://www.mqasem.net/sat/winsat/ WinSAT v2.04]: A Windows-based SAT application made particularly for researchers. | |||
=== Conferences === | |||
International Conference on Theory and Applications of Satisfiability Testing: | |||
* [http://sat2013.cs.helsinki.fi/ SAT 2013] | |||
* [http://sat2012.fbk.eu SAT 2012] | |||
* [http://www.lri.fr/SAT2011/ SAT 2011] | |||
* [http://ie.technion.ac.il/SAT10/ SAT 2010] | |||
* [http://www.cs.swansea.ac.uk/~csoliver/SAT2009/ SAT 2009] | |||
* [http://wwwcs.uni-paderborn.de/cs/ag-klbue/en/workshops/sat-08/sat08-main.php SAT 2008] | |||
* [http://sat07.ecs.soton.ac.uk/ SAT 2007] | |||
=== Publications === | |||
* [http://jsat.ewi.tudelft.nl Journal on Satisfiability, Boolean Modeling and Computation] | |||
* [http://www.ictp.trieste.it/~zecchina/SP/ Survey Propagation] | |||
=== Benchmarks === | |||
* [http://www.nlsde.buaa.edu.cn/~kexu/benchmarks/benchmarks.htm Forced Satisfiable SAT Benchmarks] | |||
* [http://www.satlib.org SATLIB] | |||
* [http://www.cs.ubc.ca/~babic/index_benchmarks.htm Software Verification Benchmarks] | |||
* [http://www.aloul.net/benchmarks.html Fadi Aloul SAT Benchmarks] | |||
SAT solving in general: | |||
* http://www.satlive.org | |||
* http://www.satisfiability.org | |||
=== Evaluation of SAT solvers === | |||
* [http://www.maxsat.udl.cat/ Yearly evaluation of SAT solvers] | |||
* [http://www.maxsat.udl.cat/08/ms08.pdf SAT solvers evaluation results for 2008] | |||
* [http://www.satcompetition.org International SAT Competitions] | |||
* [http://www.satcompetition.org/2002/onlinereport/node2.html History] | |||
More information on SAT: | |||
* [http://www.mqasem.net/sat/sat SAT and MAX-SAT for the Lay-researcher] | |||
---- | |||
''This article includes material from a column in the ACM [http://www.sigda.org SIGDA] [http://www.sigda.org/newsletter/index.html e-newsletter] by [http://www.eecs.umich.edu/~karem Prof. Karem Sakallah] <br /> | |||
Original text is available [http://www.sigda.org/newsletter/2006/eNews_061201.html here]'' | |||
{{logic}} | |||
{{DEFAULTSORT:Boolean Satisfiability Problem}} | |||
[[Category:Boolean algebra]] | |||
[[Category:Electronic design automation]] | |||
[[Category:Formal methods]] | |||
[[Category:Logic in computer science]] | |||
[[Category:NP-complete problems]] | |||
[[Category:Satisfiability problems]] | |||
Revision as of 20:27, 29 January 2014
Name: Jodi Junker
My age: 32
Country: Netherlands
Home town: Oudkarspel
Post code: 1724 Xg
Street: Waterlelie 22
my page - www.hostgator1centcoupon.info
In computer science, Boolean, or propositional, satisfiability (often written SATISFIABILITY or abbreviated SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it establishes if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE. If no such assignments exist, the function expressed by the formula is identically FALSE for all possible variable assignments. In this latter case, it is called unsatisfiable, otherwise satisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
SAT was the first known example of an NP-complete problem. That briefly means that there is no known algorithm that efficiently solves all instances of SAT, and it is generally believed (but not proven, see P versus NP problem) that no such algorithm can exist. Further, a wide range of other naturally occurring decision and optimization problems can be transformed into instances of SAT. A class of algorithms called SAT solvers can efficiently solve a large enough subset of SAT instances to be useful in various practical areas such as circuit design and automatic theorem proving, by solving SAT instances made by transforming problems that arise in those areas. Extending the capabilities of SAT solving algorithms is an ongoing area of research. However, no current such methods can efficiently solve all SAT instances.
Basic definitions and terminology
A propositional logic formula, also called Boolean expression, is built from variables, operators AND (conjunction, also denoted by ∧), OR (disjunction, ∨), NOT (negation, ¬), and parentheses. A formula is said to be satisfiable if it can be made TRUE by assigning appropriate logical values (i.e. TRUE, FALSE) to its variables. The Boolean satisfiability problem (SAT) is, given a formula, to check whether it is satisfiable. This decision problem is of central importance in various areas of computer science, including theoretical computer science, complexity theory, algorithmics, and artificial intelligence.
There are several special cases of the Boolean satisfiability problem in which the formulas are required to have a particular structure. A literal is either a variable, then called positive literal, or the negation of a variable, then called negative literal. A clause is a disjunction of literals (or a single literal). A clause is called Horn clause if it contains at most one positive literal. A formula is in conjunctive normal form (CNF) if it is a conjunction of clauses (or a single clause). For example, "x1" is a positive literal, "¬x2" is a negative literal, "x1 ∨ ¬x2" is a clause, and "(x1 ∨ ¬x2) ∧ (¬x1 ∨ x2 ∨ x3) ∧ ¬x1" is a formula in conjunctive normal form, its 1st and 3rd clause is a Horn clause, but its 2nd clause is not. The formula is satisfiable, choosing x1=FALSE, x2=FALSE, and x3 arbitrarily, since (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ x3) ∧ ¬FALSE evaluates to (FALSE ∨ TRUE) ∧ (TRUE ∨ FALSE ∨ x3) ∧ TRUE, and in turn to TRUE ∧ TRUE ∧ TRUE (i.e. to TRUE). In contrast, the CNF formula a ∧ ¬a, consisting of two clauses of one literal, is unsatisfiable, since for a=TRUE and a=FALSE it evaluates to TRUE ∧ ¬TRUE (i.e. to FALSE) and FALSE ∧ ¬FALSE (i.e. again to FALSE), respectively.
For some versions of the SAT problem, it is useful to define the notion of a generalized conjunctive normal form formula, viz. as a conjunction of arbitrarily many generalized clauses, the latter being of the form R(l1,...,ln) for some boolean operator R and (ordinary) literals li. Different sets of allowed boolean operators lead to different problem versions. As an example, R(¬x,a,b) is a generalized clause, and R(¬x,a,b) ∧ R(b,y,c) ∧ R(c,d,¬z) is a generalized conjunctive normal form. This formula is used below, with R being the ternary operator that is TRUE just if exactly one of its arguments is.
Using the laws of Boolean algebra, every propositional logic formula can be transformed into an equivalent conjunctive normal form, which may, however, be exponentially longer. For example, transforming the formula (x1∧y1) ∨ (x2∧y2) ∨ ... ∨ (xn∧yn) into conjunctive normal form yields (x1∨x2∨…∨xn) ∧ (y1∨x2∨…∨xn) ∧ (x1∨y2∨…∨xn) ∧ (y1∨y2∨…∨xn) ∧ ... ∧ (x1∨x2∨…∨yn) ∧ (y1∨x2∨…∨yn) ∧ (x1∨y2∨…∨yn) ∧ (y1∨y2∨…∨yn); while the former is a disjunction of n conjunctions of 2 variables, the latter consists of 2n clauses of n variables.
Complexity and restricted versions
Unrestricted satisfiability (SAT)
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
SAT was the first known NP-complete problem, as proved by Stephen Cook in 1971[1] and independently by Leonid Levin in 1973.[2] Until that time, the concept of an NP-complete problem did not even exist. The proof shows how every decision problem in the complexity class NP can be reduced to the SAT problem for CNF[note 1] formulas. A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, deciding whether a given graph has a 3-coloring is another problem in NP; if a graph has 17 valid 3-colorings, the SAT formula produced by the Cook–Levin reduction will have 17 satisfying assignments.
NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See Algorithms for solving SAT below.
SAT is trivial if the formulas are restricted to those in disjunctive normal form, that is, they are disjunction of conjunctions of literals. Such a formula is indeed satisfiable if and only if at least one of its conjunctions is satisfiable, and a conjunction is satisfiable if and only if it does not contain both x and NOT x for some variable x. This can be checked in linear time. Furthermore, if they are restricted to being in full disjunctive normal form, in which every variable appears exactly once in every conjunction, they can be checked in constant time (each conjunction represents one satisfying assignment). But it can take exponential time and space to convert a general SAT problem to disjunctive normal form; for an example exchange "∧" and "∨" in the above exponential blow-up example for conjunctive normal forms.
3-satisfiability

Like the satisfiability problem for arbitrary formulas, determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete also; this problem is called 3-SAT, 3CNFSAT, or 3-satisfiability. To reduce the unrestricted SAT problem to 3-SAT, transform each clause "l1 ∨ ... ∨ ln" to a conjunction of n-2 clauses "(l1 ∨ l2 ∨ x2) ∧ (¬x2 ∨ l3 ∨ x3) ∧ (¬x3 ∨ l4 ∨ x4) ∧ ... ∧ (¬xn-3 ∨ ln-2 ∨ xn-2) ∧ (¬xn-2 ∨ ln-1 ∨ ln)", where x2,...,xn-2 are fresh variables not occurring elsewhere. Although both formulas are not logically equivalent, they are equisatisfiable. The formula resulting from transforming all clauses is at most 3 times as long as its original, i.e. the length growth is polynomial.[3]
3-SAT is one of Karp's 21 NP-complete problems, and it is used as a starting point for proving that other problems are also NP-hard.[note 2] This is done by polynomial-time reduction from 3-SAT to the other problem. An example of a problem where this method has been used is the clique problem: given a CNF formula consisting of c clauses, the corresponding graph consists of a vertex for each literal, and an edge between each two non-contradicting[note 3] literals from different clauses, cf. picture. The graph has a c-clique if and only if the formula is satisfiable.Template:Refn
There is a simple randomized algorithm due to Schöning (1999) that runs in time (4/3)n where n is the number of clauses and succeeds with high probability to correctly decide 3-SAT.[4]
The exponential time hypothesis is that no algorithm can solve 3-SAT faster than o(exp(n)).
Selman, Mitchell, and Levesque (1996) give empirical data on the difficulty of randomly generated 3-SAT formulas, depending on their size parameters. Difficuly is measured in number recursive calls made by a DPLL algorithm.[5]
3-satisfiability can be generalized to k-satisfiability (k-SAT), when formulas in CNF are considered with each clause containing up to k literals. However, since for any k≥3, this problem can neither be easier than 3-SAT nor harder than SAT, and the latter two are NP-complete, so must be k-SAT.
Some authors restrict k-SAT to CNF formulas with exactly k literals. This doesn't lead to a different complexity class either, as each clause "l1 ∨ ... ∨ lj" with j<k literals can be padded with fixed dummy variables to "l1 ∨ ... ∨ lj ∨ dj+1 ∨ ... ∨ dk". After padding all clauses, 2k-1 extra clauses[note 4] have to be appended to ensure that only d1=...=dk=FALSE can lead to a satisfying assignment. Since k doesn't depend on the formula length, the extra clauses lead to a constant increase in length. For the same reason, it does not matter whether duplicate literals are allowed in clauses (like e.g. "¬x ∨ ¬y ∨ ¬y"), or not.
Exactly-1 3-satisfiability

A variant of the 3-satisfiability problem is the one-in-three 3-SAT (also known variously as 1-in-3-SAT and exactly-1 3-SAT). Given a conjunctive normal form, the problem is to determine whether there exists a truth assignment to the variables so that each clause has exactly one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has at least one TRUE literal. Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator R that is TRUE just if exactly one of its arguments is.
One-in-three 3-SAT is listed as NP-complete problem "LO4" in the standard reference, Computers and Intractability: A Guide to the Theory of NP-Completeness by Michael R. Garey and David S. Johnson. It was proved to be NP-complete by Thomas J. Schaefer as a special case of Schaefer's dichotomy theorem, which asserts that any problem generalizing Boolean satisfiability in a certain way is either in the class P or is NP-complete.[6]
Schaefer gives a construction allowing an easy polynomial-time reduction from 3-SAT to one-in-three 3-SAT. Let "(x or y or z)" be a clause in a 3CNF formula. Add six fresh boolean variables a, b, c, d, e, and f, to be used to simulate this clause and no other. Then the formula R(x,a,d) ∧ R(y,b,d) ∧ R(a,b,e) ∧ R(c,d,f) ∧ R(z,c,FALSE) is satisfiable by some setting of the fresh variables if and only if at least one of x, y, or z is TRUE, see picture (left). Thus any 3-SAT instance with m clauses and n variables may be converted into an equisatisfiable one-in-three 3-SAT instance with 5m clauses and n+6m variables.[7] Another reduction involves only four fresh variables and three clauses: R(¬x,a,b) ∧ R(b,y,c) ∧ R(c,d,¬z), see picture (right).
The one-in-three 3-SAT problem is often used in the literature as a known NP-complete problem in a reduction to show that other problems are NP-complete.Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park.
2-satisfiability
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
SAT is easier if the number of literals in a clause is limited to at most 2, in which case the problem is called 2-SAT. This problem can be solved in polynomial time, and in fact is complete for the complexity class NL. If additionally all OR operations in literals are changed to XOR operations, the result is called exclusive-or 2-satisfiability, which is a problem complete for the complexity class SL = L.
Horn-satisfiability
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church.
The problem of deciding the satisfiability of a given conjunction of Horn clauses is called Horn-satisfiability, or HORN-SAT. It can be solved in polynomial time by a single step of the Unit propagation algorithm, which produces the single minimal model of the set of Horn clauses (w.r.t. the set of literals assigned to TRUE). Horn-satisfiability is P-complete. It can be seen as P's version of the Boolean satisfiability problem.
Horn clauses are of interest because they are able to express implication of one variable from a set of other variables. Indeed, one such clause ¬x1 ∨ ... ∨ ¬xn ∨ y can be rewritten as x1 ∧ ... ∧ xn → y, that is, if x1,...,xn are all TRUE, then y needs to be TRUE as well.
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. For example, (x1 ∨ ¬x2) ∧ (¬x1 ∨ x2 ∨ x3) ∧ ¬x1 is not a Horn formula, but can be renamed to the Horn formula (x1 ∨ ¬x2) ∧ (¬x1 ∨ x2 ∨ ¬y3) ∧ ¬x1 by introducing y3 as negation of x3. In contrast, no renaming of (x1 ∨ ¬x2 ∨ ¬x3) ∧ (¬x1 ∨ x2 ∨ x3) ∧ ¬x1 leads to a Horn formula. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
XOR-satisfiability
| Solving an XOR-SAT example by Gaussian elimination | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Another special case is the class of problems where each clause contains XOR (i.e. exclusive or) rather than (plain) OR operators.[note 5] This is in P, since an XOR-SAT formula can also be viewed as a system of linear equations mod 2, and can be solved in cubic time by Gaussian elimination, see box for an example.Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park. This recast is based on the kinship between Boolean algebras and Boolean rings. Since a XOR b XOR c evaluates to TRUE if and only if exactly 1 or 3 members of {a,b,c} are TRUE, each solution of the 1-in-3-SAT problem for a given CNF formula is also a solution of the XOR-3-SAT problem, and in turn each solution of XOR-3-SAT is a solution of 3-SAT, cf. picture. As a consequence, for each CNF formula, either the 3-SAT problem or the 1-in-3-SAT problem can be decided in cubic time to be solvable or unsolvable, respectively.Template:Clarify
Provided that the complexity classes P and NP are not equal, neither 2-, nor Horn-, nor XOR-satisfiability is NP-complete, unlike SAT. The assumption that P and NP are not equal is currently not proven.
Schaefer's dichotomy theorem
Mining Engineer (Excluding Oil ) Truman from Alma, loves to spend time knotting, largest property developers in singapore developers in singapore and stamp collecting. Recently had a family visit to Urnes Stave Church. The restrictions above (CNF, 2CNF, 3CNF, Horn, XOR-SAT) bound the considered formulae to be conjunction of subformulae; each restriction states a specific form for all subformulae: for example, only binary clauses can be subformulae in 2CNF.
Schaefer's dichotomy theorem states that, for any restriction to Boolean operators that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF, Horn, and XOR-SAT formulae are special cases of this theorem.
Extensions of SAT
An extension that has gained significant popularity since 2003 is Satisfiability modulo theories (SMT) that can enrich CNF formulas with linear constraints, arrays, all-different constraints, uninterpreted functions,[8] etc. Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints.
The satisfiability problem becomes more difficult if both "for all" (∀) and "there exists" (∃) quantifiers are allowed to bind the Boolean variables. An example of such an expression would be "∀x ∀y ∃z (x ∨ y ∨ z) ∧ (¬x ∨ ¬y ∨ ¬z)"; it is valid, since for all values of x and y, an appropriate value of z can be found, viz. z=TRUE if both x and y are FALSE, and z=FALSE else. SAT itself (tacitly) uses only ∃ quantifiers. If only ∀ quantifiers are allowed instead, the so-called tautology problem is obtained, which is Co-NP-complete. If both quantifiers are allowed, the problem is called the quantified Boolean formula problem (QBF), which can be shown to be PSPACE-complete. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved.
A number of variants deal with the number of variable assignments making the formula TRUE. Ordinary SAT asks if there is at least one such assignment. MAJ-SAT, which asks if the majority of all assignments make the formula TRUE, is complete for PP, a probabilistic class. The problem of how many variable assignments satisfy a formula, not a decision problem, is in #P. UNIQUE-SAT is the problem of determining whether a formula has exactly one assignment, it is complete for US.Template:Clarify When the input is restricted to formulas having at most one satisfying assignment (or none), the problem is called UNAMBIGOUS-SAT. A solving algorithm for UNAMBIGOUS-SAT is allowed to exhibit any behavior, including endless looping, on a formula having several satisfying assignments. Although this problem seems easier, Valiant and Vazirani have shown[9] that if there is a practical (i.e. randomized polynomial-time) algorithm to solve it, then all problems in NP can be solved just as easily.
The maximum satisfiability problem, an FNP generalization of SAT, asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient approximation algorithms, but is NP-hard to solve exactly. Worse still, it is APX-complete, meaning there is no polynomial-time approximation scheme (PTAS) for this problem unless P=NP.
Other generalisations include satisfiability for first- and second-order logic, constraint satisfaction problems, 0-1 integer programming.
Self-reducibility
The SAT problem is self-reducible, that is, each algorithm which correctly answers if an instance of SAT is solvable can be used to find a satisfying assignment. First, the question is asked on the given formula Φ. If the answer is "no", the formula is unsatisfiable. Otherwise, the question is asked on the partly instantiated formula Φ{x1=TRUE}, i.e. Φ with the first variable x1 replaced by TRUE, and simplified accordingly. If the answer is "yes", then x1=TRUE, otherwise x1=FALSE. Values of other variables can be found subsequently in the same way. In total, n+1 runs of the algorithm are required, where n is the number of distinct variables in Φ.
This property of self-reducibility is used in several theorems in complexity theory:
Algorithms for solving SAT
Since the SAT problem is NP-complete, only algorithms with exponential worst-case complexity are known for it. In spite of this state of the art in complexity theory, efficient and scalable algorithms for SAT were developed over the last decade and have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints (i.e. clauses).Potter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park. Examples of such problems in electronic design automation (EDA) include formal equivalence checking, model checking, formal verification of pipelined microprocessors,[8] automatic test pattern generation, routing of FPGAs,[10] planning, and scheduling problems, and so on. A SAT-solving engine is now considered to be an essential component in the EDA toolbox.
There are two classes of high-performance algorithms for solving instances of SAT in practice: the conflict-driven clause learning algorithm, which can be viewed as a modern variant of the DPLL algorithm (well known implementation include Chaff,[11] GRASP)[12] and stochastic local search algorithms, such as WalkSAT.
A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 60s (see references below) and is now commonly referred to as the Davis–Putnam–Logemann–Loveland algorithm ("DPLL" or "DLL").[13][14] Theoretically, exponential lower bounds have been proved for the DPLL family of algorithms.
In contrast, randomized algorithms like the PPSZ algorithm by Paturi, Pudlak, Saks, and Zane set variables in a random order according to some heuristics, for example bounded-width resolution. If the heuristic can't find the correct setting, the variable is assigned randomly. The PPSZ algorithm has a runtime of for 3-SAT with a single satisfying assignment. Currently this is the best known runtime for this problem. In the setting with many satisfying assignments the randomized algorithm by Schöning has a better bound.[4][15]
Modern SAT solvers (developed in the last ten years) come in two flavors: "conflict-driven" and "look-ahead".Template:Clarify Conflict-driven solvers augment the basic DPLL search algorithm with efficient conflict analysis, clause learning, non-chronological backtracking (aka backjumping), as well as "two-watched-literals" unit propagation, adaptive branching, and random restarts. These "extras" to the basic systematic search have been empirically shown to be essential for handling the large SAT instances that arise in electronic design automation (EDA). Look-ahead solvers have especially strengthened reductions (going beyond unit-clause propagation) and the heuristics, and they are generally stronger than conflict-driven solvers on hard instances (while conflict-driven solvers can be much better on large instances which actually have an easy instance inside).
Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others. Powerful solvers are readily available as free and open source software. In particular, the conflict-driven MiniSAT, which was relatively successful at the 2005 SAT competition, only has about 600 lines of code. A modern Parallel SAT solver is ManySAT. It can achieve super linear speed-ups on important classes of problems. An example for look-ahead solvers is march_dl, which won a prize at the 2007 SAT competition.
Certain types of large random satisfiable instances of SAT can be solved by survey propagation (SP). Particularly in hardware design and verification applications, satisfiability and other logical properties of a given propositional formula are sometimes decided based on a representation of the formula as a binary decision diagram (BDD).
Almost all SAT solvers include time-outs, so they will terminate in reasonable time even if they cannot find a solution. Different SAT solvers will find different instances easy or hard, and some excel at proving unsatisfiability, and others at finding solutions. All of these behaviors can be seen in the SAT solving contests.[16]
See also
Notes
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro. References are ordered by date of publication: Template:Refbegin
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 A9.1: LO1 – LO7, pp. 259 – 260. - Template:Cite doi
- Template:Cite doi
- Template:Cite doi
- Template:Cite doi
- Template:Cite doi
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
See also
External links
SAT problem format
A SAT problem is often described in the DIMACS-CNF format: an input file in which each line represents a single disjunction. For example, a file with the two lines
1 -5 4 0 -1 5 3 4 0
represents the formula "(x1 ∨ ¬x5 ∨ x4) ∧ (¬x1 ∨ x5 ∨ x3 ∨ x4)".
Another common format for this formula is the 7-bit ASCII representation "(x1 | ~x5 | x4) & (~x1 | x5 | x3 | x4)".
BCSAT is a tool that converts input files in human-readable format to the DIMACS-CNF format.
Online SAT solvers
- BoolSAT – Solves formulas in the DIMACS-CNF format or in a more human-friendly format: "a and not b or a". Runs on a server.
- minisat-in-your-browser – Solves formulas in the DIMACS-CNF format. Runs on the browser.
Offline SAT solvers
- MiniSAT – DIMACS-CNF format.
- Lingeling – won a gold medal in a 2011 SAT competition.
- PicoSAT – an earlier solver from the Lingeling group.
- Sat4j – DIMACS-CNF format. Java source code available.
- Glucose – DIMACS-CNF format.
- RSat – won a gold medal in a 2007 SAT competition.
- UBCSAT. Supports unweighted and weighted clauses, both in the DIMACS-CNF format. C source code hosted on GitHub.
- CryptoMiniSat – won a gold medal in a 2011 SAT competition. C++ source code hosted on GitHub. Tries to put many useful features of MiniSat 2.0 core, PrecoSat ver 236, and Glucose into one package, adding many new features
- Spear – Supports bit-vector arithmetic. Can use the DIMACS-CNF format or the Spear format.
- HyperSAT – Written to experiment with B-cubing search space pruning. Won 3rd place in a 2005 SAT competition. An earlier and slower solver from the developers of Spear.
- BASolver
- ArgoSAT
- Fast SAT Solver – based on genetic algorithms.
- zChaff – not supported anymore.
- BCSAT – human-readable boolean circuit format (also converts this format to the DIMACS-CNF format and automatically links to MiniSAT or zChaff).
SAT applications
- WinSAT v2.04: A Windows-based SAT application made particularly for researchers.
Conferences
International Conference on Theory and Applications of Satisfiability Testing:
Publications
Benchmarks
SAT solving in general:
Evaluation of SAT solvers
- Yearly evaluation of SAT solvers
- SAT solvers evaluation results for 2008
- International SAT Competitions
- History
More information on SAT:
This article includes material from a column in the ACM SIGDA e-newsletter by Prof. Karem Sakallah
Original text is available here
- ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang (pdf) Not perhaps one of the best-identified of Singapore points of interest, the Spice Garden at Fort Canning Park is a veritable trove of Singapore's natural historical past, with over 100 varieties of vegetation and trees lining its trails.
There isn't a double taxation here. Property tax is imposed based mostly on property possession. It is totally different from revenue tax on the rental income, which is a tax on the income which an individual earns. It's free, and you will automatically receive property market updates, the most recent actual property developments, new guidelines and insurance policies, and lots of extra. Find out more On the similar time, monetary institutions have been lengthening the tenures of residential property loans. Over the past three years, the typical tenure for brand spanking new residential property loans has increased from 25 to 29 years. Greater than 45% of new residential property loans granted by financial establishments have tenures exceeding 30 years. Pasir Ris, Simei, Tampines Lease Property District 19 Related Articles
Mr Tharman Shanmugaratnam, Chairman of MAS, said, "Monetary conditions worldwide are removed from normal. QE3 and low rates of interest have made credit simple, but this may finally change. We're taking this step now to require extra prudent lending, and will continue to observe the property market rigorously. We will do what it takes to cool the market, and keep away from a bubble that will ultimately harm borrowers and destabilise our financial system." Rising office sector leads real property market performance, while prime retail and business park segments reasonable and residential sector continues in decline Opportunity to amass a row of 3 adjoining store houses within Little India Conservation Space D10) Holland / Tanglin HDB Frequent Room with Aircon
b. A property held by 2 or extra persons as tenants in frequent means that each proprietor has a specified or distinct share or proportion in the property. For instance, such share might be on an equal basis (50%-50%) or 90% - 10% basis and so on. Each owner might be able to dispose his share within the property both by sale or under his Will. Upon the dying of 1 proprietor, the surviving co-owner(s) do(es) not take over the deceased's curiosity in the property as is in the case of joint tenancy. His share shall be handed below his will or in accordance with the regulation of intestacy, because the case may be.
In the meantime, inside design duties went to the group at Design Intervention. Unsurprisingly, Chan's impressive home garnered the 11th Singapore Institute of Architecture Design Award this year. "The Jury is impressed with the result of what was a really shut collaboration between architect and proprietor, which turned out to be a really up-to-date tackle a tropical language of structure." explains the judging panel along with their verdict. HONG LEONG HOLDINGS LIMITED (HLH) was established in 1968 as the group's privately held property funding and property holding car. It has developed about 40 residential properties thus far and markets/manages 12 industrial initiatives. KF Property Network Pte Ltd any condo inside a constructing; a) An condo in a building
Rates of interest are extraordinarily low, globally and in Singapore, and continue to add fuel to our property market. We've to take this additional spherical of measures now, to examine current market tendencies and keep away from a extra serious correction in costs further down the road,ђ mentioned Deputy Prime Minister and Minister for Finance Tharman Shanmugaratnam. See your Banker to have an evaluation of your monetary state of affairs. Decide on the range of Property you might be keen to speculate. Verify for the best rate on the town or contact our accomplice bankers for help if required. >> Step 2 Resolve your wants and make your want list The lawyer's fees do not include stamp fees or disbursements properly incurred bythe lawyer. Promoting Your House or Flat 2xxxpsf view this challenge
Under the brand new property tax construction, properties with AV under $eight,000 will enjoy zero property tax. apartment in singapore reality, all homes with AVs as much as $59,000 will both pay no property tax or lower efficient property tax, as compared to the property tax payable beneath the earlier construction. The new rates shall be phased over in over two years, with the modifications taking impact on 1 January 2014 and 1 January 2015. We've got thus stored property tax as our wealth tax primarily based on property possession. Deborah Regulation from Expat Realtor shares her property market replace, plus top rental flats and houses at present out there to lease for a borrower with no excellent residential property loan. Hire Property District 14 Lease Property District 15 Rent Property District sixteen PropNex Property TV, translated into English by One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑ 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534; here: Thm.10.4 - ↑ 4.0 4.1 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - ↑ One of the biggest reasons investing in a Singapore new launch is an effective things is as a result of it is doable to be lent massive quantities of money at very low interest rates that you should utilize to purchase it. Then, if property values continue to go up, then you'll get a really high return on funding (ROI). Simply make sure you purchase one of the higher properties, reminiscent of the ones at Fernvale the Riverbank or any Singapore landed property Get Earnings by means of Renting
In its statement, the singapore property listing - website link, government claimed that the majority citizens buying their first residence won't be hurt by the new measures. Some concessions can even be prolonged to chose teams of consumers, similar to married couples with a minimum of one Singaporean partner who are purchasing their second property so long as they intend to promote their first residential property. Lower the LTV limit on housing loans granted by monetary establishments regulated by MAS from 70% to 60% for property purchasers who are individuals with a number of outstanding housing loans on the time of the brand new housing purchase. Singapore Property Measures - 30 August 2010 The most popular seek for the number of bedrooms in Singapore is 4, followed by 2 and three. Lush Acres EC @ Sengkang
Discover out more about real estate funding in the area, together with info on international funding incentives and property possession. Many Singaporeans have been investing in property across the causeway in recent years, attracted by comparatively low prices. However, those who need to exit their investments quickly are likely to face significant challenges when trying to sell their property – and could finally be stuck with a property they can't sell. Career improvement programmes, in-house valuation, auctions and administrative help, venture advertising and marketing, skilled talks and traisning are continuously planned for the sales associates to help them obtain better outcomes for his or her shoppers while at Knight Frank Singapore. No change Present Rules
Extending the tax exemption would help. The exemption, which may be as a lot as $2 million per family, covers individuals who negotiate a principal reduction on their existing mortgage, sell their house short (i.e., for lower than the excellent loans), or take part in a foreclosure course of. An extension of theexemption would seem like a common-sense means to assist stabilize the housing market, but the political turmoil around the fiscal-cliff negotiations means widespread sense could not win out. Home Minority Chief Nancy Pelosi (D-Calif.) believes that the mortgage relief provision will be on the table during the grand-cut price talks, in response to communications director Nadeam Elshami. Buying or promoting of blue mild bulbs is unlawful.
A vendor's stamp duty has been launched on industrial property for the primary time, at rates ranging from 5 per cent to 15 per cent. The Authorities might be trying to reassure the market that they aren't in opposition to foreigners and PRs investing in Singapore's property market. They imposed these measures because of extenuating components available in the market." The sale of new dual-key EC models will even be restricted to multi-generational households only. The models have two separate entrances, permitting grandparents, for example, to dwell separately. The vendor's stamp obligation takes effect right this moment and applies to industrial property and plots which might be offered inside three years of the date of buy. JLL named Best Performing Property Brand for second year running
The data offered is for normal info purposes only and isn't supposed to be personalised investment or monetary advice. Motley Fool Singapore contributor Stanley Lim would not personal shares in any corporations talked about. Singapore private home costs increased by 1.eight% within the fourth quarter of 2012, up from 0.6% within the earlier quarter. Resale prices of government-built HDB residences which are usually bought by Singaporeans, elevated by 2.5%, quarter on quarter, the quickest acquire in five quarters. And industrial property, prices are actually double the levels of three years ago. No withholding tax in the event you sell your property. All your local information regarding vital HDB policies, condominium launches, land growth, commercial property and more
There are various methods to go about discovering the precise property. Some local newspapers (together with the Straits Instances ) have categorised property sections and many local property brokers have websites. Now there are some specifics to consider when buying a 'new launch' rental. Intended use of the unit Every sale begins with 10 p.c low cost for finish of season sale; changes to 20 % discount storewide; follows by additional reduction of fiftyand ends with last discount of 70 % or extra. Typically there is even a warehouse sale or transferring out sale with huge mark-down of costs for stock clearance. Deborah Regulation from Expat Realtor shares her property market update, plus prime rental residences and houses at the moment available to lease Esparina EC @ Sengkang - ↑
55 years old Systems Administrator Antony from Clarence Creek, really loves learning, PC Software and aerobics. Likes to travel and was inspired after making a journey to Historic Ensemble of the Potala Palace.
You can view that web-site... ccleaner free download - ↑ (Schaefer, 1978), p.222, Lemma 3.5
- ↑ 8.0 8.1 R. E. Bryant, S. M. German, and M. N. Velev, Microprocessor Verification Using Efficient Decision Procedures for a Logic of Equality with Uninterpreted Functions, in Analytic Tableaux and Related Methods, pp. 1–13, 1999.
- ↑ Template:Cite doi
- ↑ Template:Cite doi
- ↑ Template:Cite doi
- ↑ Template:Cite doi
- ↑ Template:Cite doi
- ↑ Template:Cite doi
- ↑ "An improved exponential-time algorithm for k-SAT", Paturi, Pudlak, Saks, Zani
- ↑ Template:Cite web
Cite error: <ref> tags exist for a group named "note", but no corresponding <references group="note"/> tag was found