Approximate identity: Difference between revisions
en>R.e.b. →Ring theory: typo |
en>Addbot |
||
| Line 1: | Line 1: | ||
{{continuum mechanics|cTopic=[[Solid mechanics]]}} | |||
'''Mohr–Coulomb theory''' is a [[mathematical model]] (see [[yield surface]]) describing the response of brittle materials such as [[concrete]], or rubble piles, to shear [[Stress (physics)|stress]] as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.<ref>Juvinal, Robert C. & Marshek, Kurt .; Fundamentals of machine component design. – 2nd ed., 1991, pp. 217, ISBN 0-471-62281-8</ref> | |||
In [[geotechnical engineering]] it is used to define shear strength of soils and rocks at different [[effective stress]]es. | |||
In [[structural engineering]] it is used to determine failure load as well as the angle of [[fracture]] of a displacement fracture in concrete and similar materials. [[Charles-Augustin de Coulomb|Coulomb]]'s [[friction]] hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. [[Mohr's circle]] is used to determine which principal stresses that will produce this combination of shear and normal stress, and the angle of the plane in which this will occur. According to the [[principle of normality]] the stress introduced at failure will be perpendicular to the line describing the fracture condition. | |||
It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the [[angle of friction]]. This makes the strength of the material determinable by comparing the external [[mechanical work]] introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By [[conservation of energy]] the sum of these must be zero and this will make it possible to calculate the failure load of the construction. | |||
A common improvement of this model is to combine Coulomb's friction hypothesis with [[William John Macquorn Rankine|Rankine's]] principal stress hypothesis to describe a separation fracture. | |||
== History of the development == | |||
The Mohr–Coulomb theory is named in honour of [[Charles-Augustin de Coulomb]] and [[Christian Otto Mohr]]. Coulomb's contribution was a 1773 essay entitled "''Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l'architecture''" | |||
<!--C.A. Coulomb, Essai sur une application des regles des maximis et minimis a quelquels problemesde statique relatifs, a la architecture, Mem. Acad. Roy. Div. Sav., 7, 343–387, 1776.-->.<ref>AMIR R. KHOEI; <u>Computational Plasticity in Powder Forming Processes</u>; Elsevier, Amsterdam; 2005; 449 pp.</ref> | |||
Mohr developed a generalised form of the theory around the end of the 19th century.<ref>MAO-HONG YU; "''Advances in strength theories for materials under complex stress state in the 20th Century''"; <u>Applied Mechanics Reviews</u>; American Society of Mechanical Engineers, New York, U.S.A.; May 2002; '''55''' (3): pp. 169–218.</ref> | |||
As the generalised form affected the interpretation of the criterion, but not the substance of it, some texts continue to refer to the criterion as simply the ''''Coulomb criterion''''.<ref>NIELS SAABYE OTTOSEN and MATTI RISTINMAA; <u>The Mechanics of Constitutive Modeling</u>; Elsevier Science, Amsterdam, The Netherlands; 2005; pp. 165ff.</ref> | |||
== Mohr–Coulomb failure criterion == | |||
[[Image:Mohr Coulomb Yield Surface 3Da.png|300px|right|thumb|Figure 1: View of Mohr–Coulomb failure surface in 3D space of principal stresses for <math>c=2, \phi=-20^\circ</math>]] | |||
The Mohr–Coulomb<ref>Coulomb, C. A. (1776). ''Essai sur une application des regles des maximis et minimis a quelquels problemesde statique relatifs, a la architecture.'' Mem. Acad. Roy. Div. Sav., vol. 7, pp. 343–387.</ref> failure criterion represents the linear envelope that is obtained from a plot of the shear strength of a material versus the applied normal stress. This relation is expressed as | |||
:<math> | |||
\tau = \sigma~\tan(\phi) + c | |||
</math> | |||
where <math>\tau</math> is the shear strength, <math>\sigma</math> is the normal stress, <math>c</math> is the intercept of the failure envelope with the <math>\tau</math> axis, and <math>\phi</math> is the slope of the failure envelope. The quantity <math>c</math> is often called the '''cohesion''' and the angle <math>\phi</math> is called the ''' angle of internal friction '''. Compression is assumed to be positive in the following discussion. If compression is assumed to be negative then <math>\sigma</math> should be replaced with <math>-\sigma</math>. | |||
If <math>\phi = 0</math>, the Mohr–Coulomb criterion reduces to the [[Yield surface#Tresca_yield_surface|Tresca criterion]]. On the other hand, if <math>\phi = 90^\circ</math> the Mohr–Coulomb model is equivalent to the Rankine model. Higher values of <math>\phi</math> are not allowed. | |||
From [[Mohr's circle]] we have | |||
:<math> | |||
\sigma = \sigma_m - \tau_m \sin\phi ~;~~ \tau = \tau_m \cos\phi | |||
</math> | |||
where | |||
:<math> | |||
\tau_m = \cfrac{\sigma_1-\sigma_3}{2} ~;~~ \sigma_m = \cfrac{\sigma_1+\sigma_3}{2} | |||
</math> | |||
and <math>\sigma_1</math> is the maximum principal stress and <math>\sigma_3</math> is the minimum principal stress. | |||
Therefore the Mohr–Coulomb criterion may also be expressed as | |||
:<math> | |||
\tau_m = \sigma_m \sin\phi + c \cos\phi ~. | |||
</math> | |||
This form of the Mohr–Coulomb criterion is applicable to failure on a plane that is parallel to the <math>\sigma_2</math> direction. | |||
=== Mohr–Coulomb failure criterion in three dimensions === | |||
The Mohr–Coulomb criterion in three dimensions is often expressed as | |||
:<math> | |||
\left\{\begin{align} | |||
\pm\cfrac{\sigma_1 - \sigma_2}{2} & = \left[\cfrac{\sigma_1 + \sigma_2}{2}\right]\sin(\phi) + c\cos(\phi) \\ | |||
\pm\cfrac{\sigma_2 - \sigma_3}{2} & = \left[\cfrac{\sigma_2 + \sigma_3}{2}\right]\sin(\phi) + c\cos(\phi)\\ | |||
\pm\cfrac{\sigma_3 - \sigma_1}{2} & = \left[\cfrac{\sigma_3 + \sigma_1}{2}\right]\sin(\phi) + c\cos(\phi). | |||
\end{align}\right. | |||
</math> | |||
The [[Yield_surface#Mohr_–_Coulomb_yield_surface|Mohr–Coulomb failure surface]] is a cone with a hexagonal cross section in deviatoric stress space. | |||
The expressions for <math>\tau</math> and <math>\sigma</math> can be generalized to three dimensions by developing expressions for the normal stress and the resolved shear stress on a plane of arbitrary orientation with respect to the coordinate axes (basis vectors). If the unit normal to the plane of interest is | |||
:<math> | |||
\mathbf{n} = n_1~\mathbf{e}_1 + n_2~\mathbf{e}_2 + n_3~\mathbf{e}_3 | |||
</math> | |||
where <math>\mathbf{e}_i,~~ i=1,2,3</math> are three orthonormal unit basis vectors, and if the principal stresses <math>\sigma_1, \sigma_2, \sigma_3</math> are aligned with the basis vectors <math>\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3</math>, then the expressions for <math>\sigma,\tau</math> are | |||
:<math> | |||
\begin{align} | |||
\sigma & = n_1^2 \sigma_{1} + n_2^2 \sigma_{2} + n_3^2 \sigma_{3} \\ | |||
\tau & = \sqrt{(n_1\sigma_{1})^2 + (n_2\sigma_{2})^2 + (n_3\sigma_{3})^2 - \sigma^2} \\ | |||
& = \sqrt{n_1^2 n_2^2 (\sigma_1-\sigma_2)^2 + n_2^2 n_3^2 (\sigma_2-\sigma_3)^2 + | |||
n_3^2 n_1^2 (\sigma_3 - \sigma_1)^2}. | |||
\end{align} | |||
</math> | |||
The Mohr–Coulomb failure criterion can then be evaluated using the usual expression | |||
:<math> | |||
\tau = \sigma~\tan(\phi) + c | |||
</math> | |||
for the six planes of maximum shear stress. | |||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" | |||
!Derivation of normal and shear stress on a plane | |||
|- | |||
|Let the unit normal to the plane of interest be | |||
:<math> | |||
\mathbf{n} = n_1~\mathbf{e}_1 + n_2~\mathbf{e}_2 + n_3~\mathbf{e}_3 | |||
</math> | |||
where <math>\mathbf{e}_i,~~ i=1,2,3</math> are three orthonormal unit basis vectors. Then the traction vector on the plane is given by | |||
:<math> | |||
\mathbf{t} = n_i~\sigma_{ij}~\mathbf{e}_j ~~~\text{(repeated indices indicate summation)} | |||
</math> | |||
The magnitude of the traction vector is given by | |||
:<math> | |||
|\mathbf{t}| = \sqrt{ (n_j~\sigma_{1j})^2 + (n_k~\sigma_{2k})^2 + (n_l~\sigma_{3l})^2} ~~~\text{(repeated indices indicate summation)} | |||
</math> | |||
Then the magnitude of the stress normal to the plane is given by | |||
:<math> | |||
\sigma = \mathbf{t}\cdot\mathbf{n} = n_i~\sigma_{ij}~n_j ~~\text{(repeated indices indicate summation)} | |||
</math> | |||
The magnitude of the resolved shear stress on the plane is given by | |||
:<math> | |||
\tau = \sqrt{|\mathbf{t}|^2 - \sigma^2} | |||
</math> | |||
In terms of components, we have | |||
:<math> | |||
\begin{align} | |||
\sigma & = n_1^2 \sigma_{11} + n_2^2 \sigma_{22} + n_3^2 \sigma_{33} + | |||
2(n_1 n_2 \sigma_{12} + n_2 n_3 \sigma_{23} + n_3 n_1 \sigma_{31}) \\ | |||
\tau & = \sqrt{(n_1\sigma_{11} + n_2\sigma_{12} + n_3\sigma_{31})^2 + | |||
(n_1\sigma_{12} + n_2\sigma_{22} + n_3\sigma_{23})^2 + | |||
(n_1\sigma_{31} + n_2\sigma_{23} + n_3\sigma_{33})^2 - \sigma^2} | |||
\end{align} | |||
</math> | |||
If the principal stresses <math>\sigma_1, \sigma_2, \sigma_3</math> are aligned with the basis vectors <math>\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3</math>, then the expressions for <math>\sigma,\tau</math> are | |||
:<math> | |||
\begin{align} | |||
\sigma & = n_1^2 \sigma_{1} + n_2^2 \sigma_{2} + n_3^2 \sigma_{3} \\ | |||
\tau & = \sqrt{(n_1\sigma_{1})^2 + (n_2\sigma_{2})^2 + (n_3\sigma_{3})^2 - \sigma^2} \\ | |||
& = \sqrt{n_1^2 n_2^2 (\sigma_1-\sigma_2)^2 + n_2^2 n_3^2 (\sigma_2-\sigma_3)^2 + | |||
n_3^2 n_1^2 (\sigma_3 - \sigma_1)^2} | |||
\end{align} | |||
</math> | |||
|} | |||
{| border="0" | |||
|- | |||
| valign="bottom"| | |||
[[Image:Mohr Coulomb Yield Surface 3Db.png|300px|none|thumb|Figure 2: Mohr–Coulomb yield surface in the <math>\pi</math>-plane for <math>c = 2, \phi = 20^\circ</math>]] | |||
| | |||
| | |||
| valign="bottom"| | |||
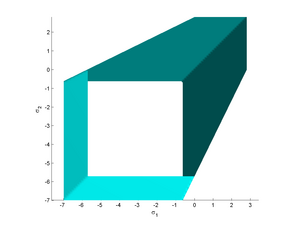
[[Image:Mohr Coulomb Yield Surface sig1sig2.png|300px|none|thumb|Figure 3: Trace of the Mohr–Coulomb yield surface in the <math>\sigma_1-\sigma_2</math>-plane for <math>c = 2, \phi = 20^\circ</math>]] | |||
|- | |||
|} | |||
== Mohr–Coulomb failure surface in Haigh–Westergaard space == | |||
The Mohr–Coulomb failure (yield) surface is often expressed in [[Yield_surface#Invariants_used_in_yield_functions|Haigh–Westergaad coordinates]]. For example, the function | |||
:<math> | |||
\cfrac{\sigma_1-\sigma_3}{2} = \cfrac{\sigma_1+\sigma_3}{2}~\sin\phi + c\cos\phi | |||
</math> | |||
can be expressed as | |||
:<math> | |||
\left[\sqrt{3}~\sin\left(\theta+\cfrac{\pi}{3}\right) - \sin\phi\cos\left(\theta+\cfrac{\pi}{3}\right)\right]\rho - \sqrt{2}\sin(\phi)\xi = \sqrt{6} c \cos\phi. | |||
</math> | |||
Alternatively, in terms of the [[Yield_surface#Invariants_used_in_yield_functions|invariants]] <math>p, q, r</math> we can write | |||
:<math> | |||
\left[\cfrac{1}{\sqrt{3}~\cos\phi}~\sin\left(\theta+\cfrac{\pi}{3}\right) - \cfrac{1}{3}\tan\phi~\cos\left(\theta+\cfrac{\pi}{3}\right)\right]q - p~\tan\phi = c | |||
</math> | |||
where | |||
:<math> | |||
\theta = \cfrac{1}{3}\arccos\left[\left(\cfrac{r}{q}\right)^3\right] ~. | |||
</math> | |||
:{| class="toccolours collapsible collapsed" width="80%" style="text-align:left" | |||
!Derivation of alternative forms of Mohr–Coulomb yield function | |||
|- | |||
|We can express the yield function | |||
:<math> | |||
\cfrac{\sigma_1-\sigma_3}{2} = \cfrac{\sigma_1+\sigma_3}{2}~\sin\phi + c\cos\phi | |||
</math> | |||
as | |||
:<math> | |||
\sigma_1~\cfrac{(1-\sin\phi)}{2~c~\cos\phi} - \sigma_3~\cfrac{(1+\sin\phi)}{2~c~\cos\phi} = 1 ~. | |||
</math> | |||
The [[Yield_surface#Invariants_used_in_yield_functions|Haigh–Westergaard invariants]] are related to the principal stresses by | |||
:<math> | |||
\sigma_1 = \cfrac{1}{\sqrt{3}}~\xi + \sqrt{\cfrac{2}{3}}~\rho~\cos\theta ~;~~ | |||
\sigma_3 = \cfrac{1}{\sqrt{3}}~\xi + \sqrt{\cfrac{2}{3}}~\rho~\cos\left(\theta+\cfrac{2\pi}{3}\right) ~. | |||
</math> | |||
Plugging into the expression for the Mohr–Coulomb yield function gives us | |||
:<math> | |||
-\sqrt{2}~\xi~\sin\phi + \rho[\cos\theta - \cos(\theta+2\pi/3)] - \rho\sin\phi[\cos\theta+\cos(\theta+2\pi/3)] = \sqrt{6}~c~\cos\phi | |||
</math> | |||
Using trigonometric identities for the sum and difference of cosines and rearrangement gives us the expression of the Mohr–Coulomb yield function in terms of <math>\xi, \rho, \theta</math>. | |||
We can express the yield function in terms of <math>p,q</math> by using the relations | |||
:<math> | |||
\xi = \sqrt{3}~p ~;~~ \rho = \sqrt{\cfrac{2}{3}}~q | |||
</math> | |||
and straightforward substitution. | |||
|} | |||
<!-- | |||
For a charge distribution an integral over the region containing the charge is equivalent to an infinite summation, treating each infinitesimal element of space as a point charge dq. | |||
For a linear charge distribution (a good approximation for charge in a wire) where <math>\lambda(\mathbf{r^\prime})</math> gives the charge per unit length at position <math>\mathbf{r^\prime}</math>, and <math>dl^\prime</math> is an infinitesimal element of length, | |||
<math> dq = \lambda(\mathbf{r^\prime})dl^\prime</math> [10] | |||
For a surface charge distribution (a good approximation for charge on a plate in a parallel plate capacitor) where <math>\sigma(\mathbf{r^\prime})</math> gives the charge per unit area at position <math>\mathbf{r^\prime}</math>, and dA^\prime is an infinitesimal element of area, | |||
<math>dq = \sigma(\mathbf{r^\prime})\,dA^\prime\,</math> | |||
For a volume charge distribution (such as charge within a bulk metal) where <math>\rho(\mathbf{r^\prime}</math>) gives the charge per unit volume at position <math>\mathbf{r^\prime}</math>, and <math>dV^\prime</math> is an infinitesimal element of volume, | |||
<math>dq = \rho(\mathbf{r^\prime})\,dV^\prime</math>[9] | |||
The force on a small test charge <math>q^\prime</math> at position <math>\mathbf{r}</math> is given by | |||
<math>\mathbf{F} = q^\prime\int dq {\mathbf{r} - \mathbf{r^\prime} \over |\mathbf{r} - \mathbf{r^\prime}|^3}</math> | |||
--> | |||
== Mohr–Coulomb yield and plasticity == | |||
The Mohr–Coulomb yield surface is often used to model the plastic flow of geomaterials (and other cohesive-frictional materials). Many such materials show dilatational behavior under triaxial states of stress which the Mohr–Coulomb model does not include. Also, since the yield surface has corners, it may be inconvenient to use the original Mohr–Coulomb model to determine the direction of plastic flow (in the [[plasticity theory|flow theory of plasticity]]). | |||
A common approach is to use a '''non-associated''' plastic flow potential that is smooth. An example of such a potential is the function{{Citation needed|date=July 2009}} | |||
:<math> | |||
g:= \sqrt{(\alpha c_\mathrm{y} \tan\psi)^2 + G^2(\phi, \theta)~ q^2} - p \tan\phi | |||
</math> | |||
where <math>\alpha</math> is a parameter, <math>c_\mathrm{y}</math> is the value of <math>c</math> when the plastic strain is zero (also called the '''initial cohesion yield stress'''), <math>\psi</math> is the angle made by the yield surface in the '''Rendulic plane''' at high values of <math>p</math> (this angle is also called the '''dilation angle'''), and <math>G(\phi,\theta)</math> is an appropriate function that is also smooth in the deviatoric stress plane. | |||
==See also== | |||
* [[3-D elasticity]] | |||
* [[Byerlee's Law]] | |||
* [[Christian Otto Mohr]]<!-- please integrate this into the article; also, who is Coulomb? --> | |||
* [[Henri Tresca]] | |||
* [[Lateral earth pressure]] | |||
* [[von Mises stress]] | |||
* [[Shear strength]] | |||
* [[Shear strength (soil)]] | |||
* [[Strain (materials science)]] | |||
* [[Stress (physics)]] | |||
* [[Yield (engineering)]] | |||
* [[Yield surface]] | |||
* [[Drucker Prager yield criterion]] — a smooth version of the M–C yield criterion | |||
==References== | |||
<references /> | |||
{{Refbegin}} | |||
* http://fbe.uwe.ac.uk/public/geocal/SoilMech/basic/soilbasi.htm | |||
* http://www.civil.usyd.edu.au/courses/civl2410/earth_pressures_rankine.doc | |||
{{Refend}} | |||
{{DEFAULTSORT:Mohr-Coulomb Theory}} | |||
[[Category:Solid mechanics]] | |||
[[Category:Plasticity]] | |||
[[Category:Materials science]] | |||
[[Category:Applied mathematics]] | |||
[[Category:Yield criteria]] | |||
Revision as of 23:54, 11 March 2013
Template:Continuum mechanics Mohr–Coulomb theory is a mathematical model (see yield surface) describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.[1]
In geotechnical engineering it is used to define shear strength of soils and rocks at different effective stresses.
In structural engineering it is used to determine failure load as well as the angle of fracture of a displacement fracture in concrete and similar materials. Coulomb's friction hypothesis is used to determine the combination of shear and normal stress that will cause a fracture of the material. Mohr's circle is used to determine which principal stresses that will produce this combination of shear and normal stress, and the angle of the plane in which this will occur. According to the principle of normality the stress introduced at failure will be perpendicular to the line describing the fracture condition.
It can be shown that a material failing according to Coulomb's friction hypothesis will show the displacement introduced at failure forming an angle to the line of fracture equal to the angle of friction. This makes the strength of the material determinable by comparing the external mechanical work introduced by the displacement and the external load with the internal mechanical work introduced by the strain and stress at the line of failure. By conservation of energy the sum of these must be zero and this will make it possible to calculate the failure load of the construction.
A common improvement of this model is to combine Coulomb's friction hypothesis with Rankine's principal stress hypothesis to describe a separation fracture.
History of the development
The Mohr–Coulomb theory is named in honour of Charles-Augustin de Coulomb and Christian Otto Mohr. Coulomb's contribution was a 1773 essay entitled "Essai sur une application des règles des maximis et minimis à quelques problèmes de statique relatifs à l'architecture" .[2] Mohr developed a generalised form of the theory around the end of the 19th century.[3] As the generalised form affected the interpretation of the criterion, but not the substance of it, some texts continue to refer to the criterion as simply the 'Coulomb criterion'.[4]
Mohr–Coulomb failure criterion

The Mohr–Coulomb[5] failure criterion represents the linear envelope that is obtained from a plot of the shear strength of a material versus the applied normal stress. This relation is expressed as
where is the shear strength, is the normal stress, is the intercept of the failure envelope with the axis, and is the slope of the failure envelope. The quantity is often called the cohesion and the angle is called the angle of internal friction . Compression is assumed to be positive in the following discussion. If compression is assumed to be negative then should be replaced with .
If , the Mohr–Coulomb criterion reduces to the Tresca criterion. On the other hand, if the Mohr–Coulomb model is equivalent to the Rankine model. Higher values of are not allowed.
From Mohr's circle we have
where
and is the maximum principal stress and is the minimum principal stress.
Therefore the Mohr–Coulomb criterion may also be expressed as
This form of the Mohr–Coulomb criterion is applicable to failure on a plane that is parallel to the direction.
Mohr–Coulomb failure criterion in three dimensions
The Mohr–Coulomb criterion in three dimensions is often expressed as
The Mohr–Coulomb failure surface is a cone with a hexagonal cross section in deviatoric stress space.
The expressions for and can be generalized to three dimensions by developing expressions for the normal stress and the resolved shear stress on a plane of arbitrary orientation with respect to the coordinate axes (basis vectors). If the unit normal to the plane of interest is
where are three orthonormal unit basis vectors, and if the principal stresses are aligned with the basis vectors , then the expressions for are
The Mohr–Coulomb failure criterion can then be evaluated using the usual expression
for the six planes of maximum shear stress.
 |
 |
Mohr–Coulomb failure surface in Haigh–Westergaard space
The Mohr–Coulomb failure (yield) surface is often expressed in Haigh–Westergaad coordinates. For example, the function
can be expressed as
Alternatively, in terms of the invariants we can write
where
Derivation of alternative forms of Mohr–Coulomb yield function We can express the yield function as
The Haigh–Westergaard invariants are related to the principal stresses by
Plugging into the expression for the Mohr–Coulomb yield function gives us
Using trigonometric identities for the sum and difference of cosines and rearrangement gives us the expression of the Mohr–Coulomb yield function in terms of .
We can express the yield function in terms of by using the relations
and straightforward substitution.
Mohr–Coulomb yield and plasticity
The Mohr–Coulomb yield surface is often used to model the plastic flow of geomaterials (and other cohesive-frictional materials). Many such materials show dilatational behavior under triaxial states of stress which the Mohr–Coulomb model does not include. Also, since the yield surface has corners, it may be inconvenient to use the original Mohr–Coulomb model to determine the direction of plastic flow (in the flow theory of plasticity).
A common approach is to use a non-associated plastic flow potential that is smooth. An example of such a potential is the functionPotter or Ceramic Artist Truman Bedell from Rexton, has interests which include ceramics, best property developers in singapore developers in singapore and scrabble. Was especially enthused after visiting Alejandro de Humboldt National Park.
where is a parameter, is the value of when the plastic strain is zero (also called the initial cohesion yield stress), is the angle made by the yield surface in the Rendulic plane at high values of (this angle is also called the dilation angle), and is an appropriate function that is also smooth in the deviatoric stress plane.
See also
- 3-D elasticity
- Byerlee's Law
- Christian Otto Mohr
- Henri Tresca
- Lateral earth pressure
- von Mises stress
- Shear strength
- Shear strength (soil)
- Strain (materials science)
- Stress (physics)
- Yield (engineering)
- Yield surface
- Drucker Prager yield criterion — a smooth version of the M–C yield criterion
References
- ↑ Juvinal, Robert C. & Marshek, Kurt .; Fundamentals of machine component design. – 2nd ed., 1991, pp. 217, ISBN 0-471-62281-8
- ↑ AMIR R. KHOEI; Computational Plasticity in Powder Forming Processes; Elsevier, Amsterdam; 2005; 449 pp.
- ↑ MAO-HONG YU; "Advances in strength theories for materials under complex stress state in the 20th Century"; Applied Mechanics Reviews; American Society of Mechanical Engineers, New York, U.S.A.; May 2002; 55 (3): pp. 169–218.
- ↑ NIELS SAABYE OTTOSEN and MATTI RISTINMAA; The Mechanics of Constitutive Modeling; Elsevier Science, Amsterdam, The Netherlands; 2005; pp. 165ff.
- ↑ Coulomb, C. A. (1776). Essai sur une application des regles des maximis et minimis a quelquels problemesde statique relatifs, a la architecture. Mem. Acad. Roy. Div. Sav., vol. 7, pp. 343–387.















![\left\{{\begin{aligned}\pm {\cfrac {\sigma _{1}-\sigma _{2}}{2}}&=\left[{\cfrac {\sigma _{1}+\sigma _{2}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{2}-\sigma _{3}}{2}}&=\left[{\cfrac {\sigma _{2}+\sigma _{3}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{3}-\sigma _{1}}{2}}&=\left[{\cfrac {\sigma _{3}+\sigma _{1}}{2}}\right]\sin(\phi )+c\cos(\phi ).\end{aligned}}\right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c803ad5abc5a66dc32e1ff2779360f2f6c76349)
















![{\displaystyle \left[{\sqrt {3}}~\sin \left(\theta +{\cfrac {\pi }{3}}\right)-\sin \phi \cos \left(\theta +{\cfrac {\pi }{3}}\right)\right]\rho -{\sqrt {2}}\sin(\phi )\xi ={\sqrt {6}}c\cos \phi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c57ba6733272e3f771a5a385f184154fb443f8a)

![{\displaystyle \left[{\cfrac {1}{{\sqrt {3}}~\cos \phi }}~\sin \left(\theta +{\cfrac {\pi }{3}}\right)-{\cfrac {1}{3}}\tan \phi ~\cos \left(\theta +{\cfrac {\pi }{3}}\right)\right]q-p~\tan \phi =c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02588542438576a372c94da0222588c1b884e8b5)
![{\displaystyle \theta ={\cfrac {1}{3}}\arccos \left[\left({\cfrac {r}{q}}\right)^{3}\right]~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/516f0f32b6affc0b964247892a7e9726680aea78)


![-{\sqrt {2}}~\xi ~\sin \phi +\rho [\cos \theta -\cos(\theta +2\pi /3)]-\rho \sin \phi [\cos \theta +\cos(\theta +2\pi /3)]={\sqrt {6}}~c~\cos \phi](https://wikimedia.org/api/rest_v1/media/math/render/svg/30acd02342cee58b1989980ffa78c543123bc00b)








