Crossing number (knot theory)
 An alternated square tiling or checkerboard pattern. Template:CDD or Template:CDD |
 An expanded square tiling. Template:CDD |
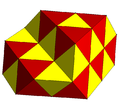 A partially filled alternated cubic honeycomb with tetrahedral and octahedral cells. Template:CDD or Template:CDD |
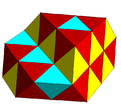 A subsymmetry colored alternated cubic honeycomb. Template:CDD |
In geometry, the alternated hypercube honeycomb (or demicubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group for n ≥ 4. A lower symmetry form can be created by removing another mirror on a order-4 peak.
The alternated hypercube facets become demihypercubes, and the deleted vertices create new orthoplex facets. The vertex figure for honeycombs of this family are rectified orthoplexes.
These are also named as hδn for an (n-1)-dimensional honeycomb.
| hδn | Name | Schläfli symbol |
Symmetry family | ||
|---|---|---|---|---|---|
[4,3n-4,31,1] |
[31,1,3n-5,31,1] | ||||
| Coxeter-Dynkin diagrams by family | |||||
| hδ2 | Apeirogon | {∞} | Template:CDD Template:CDD |
||
| hδ3 | Alternated square tiling (Same as {4,4}) |
h{4,4}=t1{4,4} t0,2{4,4} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ4 | Alternated cubic honeycomb | h{4,3,4} {31,1,4} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ5 | 16-cell tetracomb (Same as {3,3,4,3}) |
h{4,32,4} {31,1,3,4} {31,1,1,1} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ6 | 5-demicube honeycomb | h{4,33,4} {31,1,32,4} {31,1,3,31,1} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ7 | 6-demicube honeycomb | h{4,34,4} {31,1,33,4} {31,1,32,31,1} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ8 | 7-demicube honeycomb | h{4,35,4} {31,1,34,4} {31,1,33,31,1} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδ9 | 8-demicube honeycomb | h{4,36,4} {31,1,35,4} {31,1,34,31,1} |
Template:CDD Template:CDD Template:CDD |
Template:CDD | |
| hδn | n-demicubic honeycomb | h{4,3n-3,4} {31,1,3n-4,4} {31,1,3n-5,31,1} |
... | ||
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 122-123, 1973. (The lattice of hypercubes γn form the cubic honeycombs, δn+1)
- pp. 154-156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- p. 296, Table II: Regular honeycombs, δn+1
(I'm no baseball guy, but if you increase the opponent's chance of winning by intentionally putting a runner on first in that situation, how come EVERY manager does it?
The citizens of Summerside and the surrounding area derserved this facility, for too long we had to use outdated decrepit, unsafe and embarassing facilities, I applaud ethe Mayor and the Council at the time who had the vision, and the and the community spirit to push the building of this facility thru all the politics and legal stuff to get this built. And it continues to grow, The addition of a the skateboarding facility tp CUP is proving to be a well used and appreciated park for our young citizens.
http://southfloridanfp.org/coach/?key=cheap-coach-outlet-24
http://southfloridanfp.org/coach/?key=coach-gilroy-outlet-90
http://southfloridanfp.org/coach/?key=coach-sneakers-outlet-25
http://southfloridanfp.org/coach/?key=coach-bags-on-sale-at-outlet-33
http://southfloridanfp.org/coach/?key=coach-pocketbooks-outlet-64
If you adored this post and you would certainly such as to receive additional facts concerning Cheap Uggs Boots kindly go to the web site.