Mössbauer spectroscopy

Template:Distinguish2 Template:Differential equations In mathematics, finite-difference methods (FDM) are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.

Derivation from Taylor's polynomial

First, assuming the function whose derivatives are to be approximated is properly-behaved, by Taylor's theorem, we can create a Taylor Series expansion

$f(x_{0}+h)=f(x_{0})+{\frac {f'(x_{0})}{1!}}h+{\frac {f^{(2)}(x_{0})}{2!}}h^{2}+\cdots +{\frac {f^{(n)}(x_{0})}{n!}}h^{n}+R_{n}(x),$

where n! denotes the factorial of n, and R_n(x) is a remainder term, denoting the difference between the Taylor polynomial of degree n and the original function. We will derive an approximation for the first derivative of the function "f" by first truncating the Taylor polynomial:

$f(x_{0}+h)=f(x_{0})+f'(x_{0})h+R_{1}(x),$

Setting, x₀=a and (x-a)=h we have,

$f(a+h)=f(a)+f'(a)h+R_{1}(x),$

Dividing across by h gives:

${f(a+h) \over h}={f(a) \over h}+f'(a)+{R_{1}(x) \over h}$

Solving for f'(a):

$f'(a)={f(a+h)-f(a) \over h}-{R_{1}(x) \over h}$

Assuming that $R_{1}(x)$ is sufficiently small, the approximation of the first derivative of "f" is:

$f'(a)\approx {f(a+h)-f(a) \over h}.$

Accuracy and order

DTZ's public sale group in Singapore auctions all forms of residential, workplace and retail properties, outlets, homes, lodges, boarding homes, industrial buildings and development websites. Auctions are at present held as soon as a month.

We will not only get you a property at a rock-backside price but also in an space that you've got longed for. You simply must chill out back after giving us the accountability. We will assure you 100% satisfaction. Since we now have been working in the Singapore actual property market for a very long time, we know the place you may get the best property at the right price. You will also be extremely benefited by choosing us, as we may even let you know about the precise time to invest in the Singapore actual property market.

The Hexacube is offering new ec launch singapore business property for sale Singapore investors want to contemplate. Residents of the realm will likely appreciate that they'll customize the business area that they wish to purchase as properly. This venture represents one of the crucial expansive buildings offered in Singapore up to now. Many investors will possible want to try how they will customise the property that they do determine to buy by means of here. This location has offered folks the prospect that they should understand extra about how this course of can work as well.

Singapore has been beckoning to traders ever since the value of properties in Singapore started sky rocketing just a few years again. Many businesses have their places of work in Singapore and prefer to own their own workplace area within the country once they decide to have a everlasting office. Rentals in Singapore in the corporate sector can make sense for some time until a business has discovered a agency footing. Finding Commercial Property Singapore takes a variety of time and effort but might be very rewarding in the long term.

is changing into a rising pattern among Singaporeans as the standard of living is increasing over time and more Singaporeans have abundance of capital to invest on properties. Investing in the personal properties in Singapore I would like to applaud you for arising with such a book which covers the secrets and techniques and tips of among the profitable Singapore property buyers. I believe many novice investors will profit quite a bit from studying and making use of some of the tips shared by the gurus." – Woo Chee Hoe Special bonus for consumers of Secrets of Singapore Property Gurus Actually, I can't consider one other resource on the market that teaches you all the points above about Singapore property at such a low value. Can you? Condominium For Sale (D09) – Yong An Park For Lease

In 12 months 2013, c ommercial retails, shoebox residences and mass market properties continued to be the celebrities of the property market. Models are snapped up in report time and at document breaking prices. Builders are having fun with overwhelming demand and patrons need more. We feel that these segments of the property market are booming is a repercussion of the property cooling measures no.6 and no. 7. With additional buyer's stamp responsibility imposed on residential properties, buyers change their focus to commercial and industrial properties. I imagine every property purchasers need their property funding to understand in value.

The error in a method's solution is defined as the difference between its approximation and the exact analytical solution. The two sources of error in finite difference methods are round-off error, the loss of precision due to computer rounding of decimal quantities, and truncation error or discretization error, the difference between the exact solution of the finite difference equation and the exact quantity assuming perfect arithmetic (that is, assuming no round-off).

The finite difference method relies on discretizing a function on a grid.

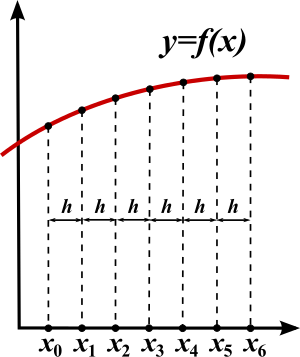
To use a finite difference method to attempt to solve (or, more generally, approximate the solution to) a problem, one must first discretize the problem's domain. This is usually done by dividing the domain into a uniform grid (see image to the right). Note that this means that finite-difference methods produce sets of discrete numerical approximations to the derivative, often in a "time-stepping" manner.

An expression of general interest is the local truncation error of a method. Typically expressed using Big-O notation, local truncation error refers to the error from a single application of a method. That is, it is the quantity $f'(x_{i})-f'_{i}$ if $f'(x_{i})$ refers to the exact value and $f'_{i}$ to the numerical approximation. The remainder term of a Taylor polynomial is convenient for analyzing the local truncation error. Using the Lagrange form of the remainder from the Taylor polynomial for $f(x_{0}+h)$, which is

$R_{n}(x_{0}+h)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(h)^{n+1}$, where $x_{0}<\xi <x_{0}+h$,

the dominant term of the local truncation error can be discovered. For example, again using the forward-difference formula for the first derivative, knowing that $f(x_{i})=f(x_{0}+ih)$,

$f(x_{0}+ih)=f(x_{0})+f'(x_{0})ih+{\frac {f''(\xi )}{2!}}(ih)^{2},$

and with some algebraic manipulation, this leads to

${\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+{\frac {f''(\xi )}{2!}}ih,$

and further noting that the quantity on the left is the approximation from the finite difference method and that the quantity on the right is the exact quantity of interest plus a remainder, clearly that remainder is the local truncation error. A final expression of this example and its order is:

${\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+O(h).$

This means that, in this case, the local truncation error is proportional to the step size.

Example: ordinary differential equation

For example, consider the ordinary differential equation

$u'(x)=3u(x)+2.\,$

The Euler method for solving this equation uses the finite difference quotient

${\frac {u(x+h)-u(x)}{h}}\approx u'(x)$

to approximate the differential equation by first substituting in for u'(x) and applying a little algebra to get

$u(x+h)=u(x)+h(3u(x)+2).\,$

The last equation is a finite-difference equation, and solving this equation gives an approximate solution to the differential equation.

Example: The heat equation

Consider the normalized heat equation in one dimension, with homogeneous Dirichlet boundary conditions

$U_{t}=U_{xx}\,$

$U(0,t)=U(1,t)=0\,$ (boundary condition)

$U(x,0)=U_{0}(x)\,$ (initial condition)

One way to numerically solve this equation is to approximate all the derivatives by finite differences. We partition the domain in space using a mesh $x_{0},...,x_{J}$ and in time using a mesh $t_{0},....,t_{N}$. We assume a uniform partition both in space and in time, so the difference between two consecutive space points will be h and between two consecutive time points will be k. The points

$u(x_{j},t_{n})=u_{j}^{n}$

will represent the numerical approximation of $u(x_{j},t_{n}).$

Explicit method

The stencil for the most common explicit method for the heat equation.

Using a forward difference at time $t_{n}$ and a second-order central difference for the space derivative at position $x_{j}$ (FTCS) we get the recurrence equation:

${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}.\,$

This is an explicit method for solving the one-dimensional heat equation.

We can obtain $u_{j}^{n+1}$ from the other values this way:

$u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}$

where $r=k/h^{2}.$

So, with this recurrence relation, and knowing the values at time n, one can obtain the corresponding values at time n+1. $u_{0}^{n}$ and $u_{J}^{n}$ must be replaced by the boundary conditions, in this example they are both 0.

This explicit method is known to be numerically stable and convergent whenever $r\leq 1/2$. The numerical errors are proportional to the time step and the square of the space step:

$\Delta u=O(k)+O(h^{2})\,$

Implicit method

The implicit method stencil.

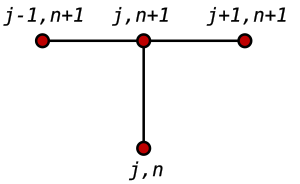
If we use the backward difference at time $t_{n+1}$ and a second-order central difference for the space derivative at position $x_{j}$ (The Backward Time, Centered Space Method "BTCS") we get the recurrence equation:

${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}.\,$

This is an implicit method for solving the one-dimensional heat equation.

We can obtain $u_{j}^{n+1}$ from solving a system of linear equations:

$(1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^{n}$

The scheme is always numerically stable and convergent but usually more numerically intensive than the explicit method as it requires solving a system of numerical equations on each time step. The errors are linear over the time step and quadratic over the space step:

$\Delta u=O(k)+O(h^{2}).\,$

Crank–Nicolson method

Finally if we use the central difference at time $t_{n+1/2}$ and a second-order central difference for the space derivative at position $x_{j}$ ("CTCS") we get the recurrence equation:

${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {1}{2}}\left({\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}\right).\,$

This formula is known as the Crank–Nicolson method.

The Crank–Nicolson stencil.

We can obtain $u_{j}^{n+1}$ from solving a system of linear equations:

$(2+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=(2-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}$

The scheme is always numerically stable and convergent but usually more numerically intensive as it requires solving a system of numerical equations on each time step. The errors are quadratic over both the time step and the space step:

$\Delta u=O(k^{2})+O(h^{2}).\,$

Usually the Crank–Nicolson scheme is the most accurate scheme for small time steps. The explicit scheme is the least accurate and can be unstable, but is also the easiest to implement and the least numerically intensive. The implicit scheme works the best for large time steps.

See also

• Finite element method
• Finite difference
• Finite difference time domain
• Stencil (numerical analysis)
• Finite difference coefficients
• Five-point stencil
• Lax–Richtmyer theorem
• Finite difference methods for option pricing
• Upwind differencing scheme for convection
• Central differencing scheme

References

43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.

• K.W. Morton and D.F. Mayers, Numerical Solution of Partial Differential Equations, An Introduction. Cambridge University Press, 2005.
• Oliver Rübenkönig, The Finite Difference Method (FDM) - An introduction, (2006) Albert Ludwigs University of Freiburg
• Autar Kaw and E. Eric Kalu, Numerical Methods with Applications, (2008) [1]

External links

• List of Internet Resources for the Finite Difference Method for PDEs
• Finite Difference Method of Solving ODEs (Boundary Value Problems) Notes, PPT, Maple, Mathcad, Matlab, Mathematica
• Lecture Notes Shih-Hung Chen, National Central University
• Randall J. LeVeque, Finite Difference Methods for Ordinary and Partial Differential Equations, SIAM, 2007.
• Finite Difference Method
• Finite Difference Method for Boundary Value Problems
• Finite Difference Methodology in Materials Science