Lotka–Volterra equation: Difference between revisions
en>DonAByrd m Clarify wording of explanation of dx/dt, dy/dt and of parameters |
en>Joe Schmedley m fmt |
||
| Line 1: | Line 1: | ||
In [[geometry]], an '''inscribed angle''' is formed when two [[secant line]]s of a [[circle]] (or, in a [[degenerate case]], when one [[secant line]] and one [[tangent line]] of that circle) intersect on the circle. | |||
Typically, it is easiest to think of an inscribed angle as being defined by two [[Chord (geometry)|chords]] of the circle sharing an endpoint. | |||
The basic properties of inscribed angles are discussed in Book 3, Propositions 20–22 of [[Euclid's Elements|Euclid's ''Elements'']]. These are the inscribed angle is half the central angle, inscribed angles on the same arc of a chord are equal and the sum of the two distinct inscribed angles of a chord is 180°. | |||
==Property== | |||
An inscribed angle is said to intersect an [[Arc (geometry)|arc]] on the circle. The arc is the portion of the circle that is in the interior of the angle. The measure of the [[intercepted arc]] (equal to its [[central angle]]) is exactly twice the measure of the inscribed angle. | |||
This single property has a number of consequences within the circle. For example, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal. It also allows one to prove that the opposite angles of a [[cyclic quadrilateral]] are [[Supplementary angles|supplementary]]. | |||
==Proof== | |||
To understand this proof, it is useful to draw a diagram. | |||
===Inscribed angles where one chord is a diameter=== | |||
[[Image:InscribedAngle 1ChordDiam.svg|right]] | |||
Let ''O'' be the center of a circle. Choose two points on the circle, and call them ''V'' and ''A''. Draw line ''VO'' and extended past ''O'' so that it intersects the circle at point ''B'' which is [[diametrically opposite]] the point ''V''. Draw an angle whose [[Vertex (geometry)|vertex]] is point ''V'' and whose sides pass through points ''A'' and ''B''. | |||
Draw line ''OA''. Angle ''BOA'' is a [[central angle]]; call it ''θ''. Lines ''OV'' and ''OA'' are both [[radius|radii]] of the circle, so they have equal lengths. Therefore triangle ''VOA'' is [[isosceles]], so angle ''BVA'' (the inscribed angle) and angle ''VAO'' are equal; let each of them be denoted as ''ψ''. | |||
Angles ''BOA'' and ''AOV'' are [[supplementary angle|supplementary]]. They add up to 180°, since line ''VB'' passing through ''O'' is a straight line. Therefore angle ''AOV'' measures 180° − ''θ''. | |||
It is known that the three angles of a [[triangle]] add up to 180°, and the three angles of triangle ''VOA'' are: | |||
: 180° − ''θ'' | |||
: ''ψ'' | |||
: ''ψ''. | |||
Therefore | |||
:<math> 2 \psi + 180^\circ - \theta = 180^\circ. </math> | |||
Subtract 180° from both sides, | |||
:<math> 2 \psi = \theta, \,</math> | |||
where ''θ'' is the central angle subtending arc ''AB'' and ''ψ'' is the inscribed angle subtending arc ''AB''. | |||
===Inscribed angles with the center of the circle in their interior=== | |||
[[Image:InscribedAngle CenterCircle.svg|right]] | |||
Given a circle whose center is point ''O'', choose three points ''V'', ''C'', and ''D'' on the circle. Draw lines ''VC'' and ''VD'': angle ''DVC'' is an inscribed angle. Now draw line ''VO'' and extend it past point ''O'' so that it intersects the circle at point ''E''. Angle ''DVC'' subtends arc ''DC'' on the circle. | |||
Suppose this arc includes point ''E'' within it. Point ''E'' is diametrically opposite to point ''V''. Angles ''DVE'' and ''EVC'' are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them. | |||
Therefore | |||
:<math> \angle DVC = \angle DVE + \angle EVC. \, </math> | |||
then let | |||
:<math> \psi_0 = \angle DVC, </math> | |||
:<math> \psi_1 = \angle DVE, </math> | |||
:<math> \psi_2 = \angle EVC, </math> | |||
so that | |||
:<math> \psi_0 = \psi_1 + \psi_2. \qquad \qquad (1) </math> | |||
Draw lines ''OC'' and ''OD''. Angle ''DOC'' is a central angle, but so are angles ''DOE'' and ''EOC'', and | |||
:<math> \angle DOC = \angle DOE + \angle EOC. </math> | |||
Let | |||
:<math> \theta_0 = \angle DOC, </math> | |||
:<math> \theta_1 = \angle DOE, </math> | |||
:<math> \theta_2 = \angle EOC, </math> | |||
so that | |||
:<math> \theta_0 = \theta_1 + \theta_2. \qquad \qquad (2) </math> | |||
From Part One we know that <math> \theta_1 = 2 \psi_1 </math> and that <math> \theta_2 = 2 \psi_2 </math>. Combining these results with equation (2) yields | |||
:<math> \theta_0 = 2 \psi_1 + 2 \psi_2 \,</math> | |||
therefore, by equation (1), | |||
:<math> \theta_0 = 2 \psi_0. \,</math> | |||
===Inscribed angles with the center of the circle in their exterior=== | |||
[[Image:InscribedAngle CenterCircleExtV2.svg|right]] | |||
[The previous case can be extended to cover the case where the measure of the inscribed angle is the ''difference'' between two inscribed angles as discussed in the first part of this proof.] | |||
Given a circle whose center is point ''O'', choose three points ''V'', ''C'', and ''D'' on the circle. Draw lines ''VC'' and ''VD'': angle ''DVC'' is an inscribed angle. Now draw line ''VO'' and extend it past point ''O'' so that it intersects the circle at point ''E''. Angle ''DVC'' subtends arc ''DC'' on the circle. | |||
Suppose this arc does not include point ''E'' within it. Point ''E'' is diametrically opposite to point ''V''. Angles ''DVE'' and ''EVC'' are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them. | |||
Therefore | |||
:<math> \angle DVC = \angle EVC - \angle DVE </math>. | |||
then let | |||
:<math> \psi_0 = \angle DVC, </math> | |||
:<math> \psi_1 = \angle DVE, </math> | |||
:<math> \psi_2 = \angle EVC, </math> | |||
so that | |||
:<math> \psi_0 = \psi_2 - \psi_1. \qquad \qquad (3) </math> | |||
Draw lines ''OC'' and ''OD''. Angle ''DOC'' is a central angle, but so are angles ''DOE'' and ''EOC'', and | |||
:<math> \angle DOC = \angle EOC - \angle DOE. </math> | |||
Let | |||
:<math> \theta_0 = \angle DOC, </math> | |||
:<math> \theta_1 = \angle DOE, </math> | |||
:<math> \theta_2 = \angle EOC, </math> | |||
so that | |||
:<math> \theta_0 = \theta_2 - \theta_1. \qquad \qquad (4) </math> | |||
From Part One we know that <math> \theta_1 = 2 \psi_1 </math> and that <math> \theta_2 = 2 \psi_2 </math>. Combining these results with equation (4) yields | |||
:<math> \theta_0 = 2 \psi_2 - 2 \psi_1 </math> | |||
therefore, by equation (3), | |||
:<math> \theta_0 = 2 \psi_0. </math> | |||
==Theorem== | |||
[[Image:Inscribed angle theorem.svg|thumb|right|250px|The inscribed angle ''θ'' is half of the central angle 2''θ'' that subtends the same arc on the circle (magenta). Thus, the angle ''θ'' does not change as its vertex is moved around on the circle (green, blue and gold angles).]] | |||
[[File:ArcCapable.gif|thumb|350px|right|Given the two points ''A'' and ''B'', the set of points ''M'' in the plane for which the angle ''AMB'' is equal to ''α'' is an arc of a circle. The measure of the angle ''AOB'', which ''O'' is the center of the circle, is 2''α''.]] | |||
The inscribed angle theorem states that an angle ''θ'' inscribed in a circle is half of the central angle 2''θ'' that [[Subtended arc|subtend]]s the same [[Arc (geometry)|arc]] on the circle. Therefore, the angle does not change as its [[Vertex (geometry)|vertex]] is moved to different positions on the circle. | |||
The inscribed angle [[theorem]] is used in many proofs of elementary [[Euclidean geometry of the plane]]. A special case of the theorem is [[Thales' theorem]], which states that the angle subtended by a [[diameter]] is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of [[cyclic quadrilateral]]s sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the [[power of a point]] with respect to a circle. | |||
===Proof=== | |||
In the simplest case, one leg of the inscribed angle is a diameter of the circle, i.e., passes through the center of the circle. Since that leg is a straight line, the supplement of the central angle equals 180° − 2''θ''. Drawing a [[Circular segment|segment]] from the center of the circle to the other point of [[Line-line intersection|intersection]] of the inscribed angle produces an [[isosceles triangle]], made from two radii of the circle and the second leg of the inscribed angle. Since two of the angles in an isosceles triangle are equal and since the angles in a triangle must add up to 180°, it follows that the inscribed angle equals ''θ'', half of the central angle. | |||
This result may be extended to an arbitrarily inscribed angle by drawing a diameter from the vertex of the angle. This converts the general problem into two sub-cases in which a diameter is a leg of each angle. The arbitrary angle equals half of the sum of the two central angles that share the diameter as a leg. Adding the two subangles again yields the result that the inscribed angle is half of the central angle. | |||
Note that the central angle for the golden inscribed angle is 360° − 2''θ''. Therefore, the half of it (and thus the measure of the golden inscribed angle) is 180° − ''θ''. | |||
The set of all points (locus) for which a line segment can be seen at angle measured ''θ'' contains two arcs (one of each side of the line segment with central angle 2''θ''). In the special case of 90°, there is exactly one circle with center the middle of the line segment. | |||
===Corollaries=== | |||
By a similar argument, the angle between a [[Chord (geometry)|chord]] and the [[tangent]] line at one of its intersection points equals half of the central angle subtended by the chord. See also [[Tangent lines to circles]]. | |||
==References== | |||
* {{Cite book | author = Ogilvy CS | year = 1990 | title = Excursions in Geometry | publisher = Dover | isbn = 0-486-26530-7 | pages = 17–23 | postscript = <!--None-->}} | |||
* {{cite book | author = Gellert W, Küstner H, Hellwich M, Kästner H | title = The VNR Concise Encyclopedia of Mathematics | publisher = Van Nostrand Reinhold | location = New York | isbn = 0-442-22646-2 | pages = 172 | year = 1977}} | |||
==External links== | |||
* {{MathWorld |urlname=InscribedAngle |title=Inscribed Angle}} | |||
* [http://www.mathalino.com/reviewer/plane-geometry/relationship-between-central-angle-and-inscribed-angle Relationship Between Central Angle and Inscribed Angle] | |||
* [http://www.cut-the-knot.org/pythagoras/Munching/inscribed.shtml Munching on Inscribed Angles] at [[cut-the-knot]] | |||
* [http://www.mathopenref.com/arccentralangle.html Arc Central Angle] With interactive animation | |||
* [http://www.mathopenref.com/arcperipheralangle.html Arc Peripheral (inscribed) Angle] With interactive animation | |||
* [http://www.mathopenref.com/arccentralangletheorem.html Arc Central Angle Theorem] With interactive animation | |||
[[Category:Euclidean plane geometry]] | |||
[[Category:Angle]] | |||
[[Category:Circles]] | |||
[[Category:Articles containing proofs]] | |||
Revision as of 09:27, 17 January 2014
In geometry, an inscribed angle is formed when two secant lines of a circle (or, in a degenerate case, when one secant line and one tangent line of that circle) intersect on the circle.
Typically, it is easiest to think of an inscribed angle as being defined by two chords of the circle sharing an endpoint.
The basic properties of inscribed angles are discussed in Book 3, Propositions 20–22 of Euclid's Elements. These are the inscribed angle is half the central angle, inscribed angles on the same arc of a chord are equal and the sum of the two distinct inscribed angles of a chord is 180°.
Property
An inscribed angle is said to intersect an arc on the circle. The arc is the portion of the circle that is in the interior of the angle. The measure of the intercepted arc (equal to its central angle) is exactly twice the measure of the inscribed angle.
This single property has a number of consequences within the circle. For example, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal. It also allows one to prove that the opposite angles of a cyclic quadrilateral are supplementary.
Proof
To understand this proof, it is useful to draw a diagram.
Inscribed angles where one chord is a diameter
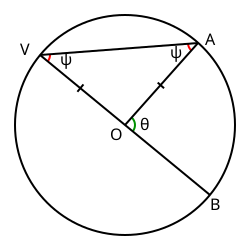
Let O be the center of a circle. Choose two points on the circle, and call them V and A. Draw line VO and extended past O so that it intersects the circle at point B which is diametrically opposite the point V. Draw an angle whose vertex is point V and whose sides pass through points A and B.
Draw line OA. Angle BOA is a central angle; call it θ. Lines OV and OA are both radii of the circle, so they have equal lengths. Therefore triangle VOA is isosceles, so angle BVA (the inscribed angle) and angle VAO are equal; let each of them be denoted as ψ.
Angles BOA and AOV are supplementary. They add up to 180°, since line VB passing through O is a straight line. Therefore angle AOV measures 180° − θ.
It is known that the three angles of a triangle add up to 180°, and the three angles of triangle VOA are:
- 180° − θ
- ψ
- ψ.
Therefore
Subtract 180° from both sides,
where θ is the central angle subtending arc AB and ψ is the inscribed angle subtending arc AB.
Inscribed angles with the center of the circle in their interior

Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past point O so that it intersects the circle at point E. Angle DVC subtends arc DC on the circle.
Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that and that . Combining these results with equation (2) yields
therefore, by equation (1),
Inscribed angles with the center of the circle in their exterior

[The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.]
Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past point O so that it intersects the circle at point E. Angle DVC subtends arc DC on the circle.
Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that and that . Combining these results with equation (4) yields
therefore, by equation (3),
Theorem


The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.
The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem, which states that the angle subtended by a diameter is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point with respect to a circle.
Proof
In the simplest case, one leg of the inscribed angle is a diameter of the circle, i.e., passes through the center of the circle. Since that leg is a straight line, the supplement of the central angle equals 180° − 2θ. Drawing a segment from the center of the circle to the other point of intersection of the inscribed angle produces an isosceles triangle, made from two radii of the circle and the second leg of the inscribed angle. Since two of the angles in an isosceles triangle are equal and since the angles in a triangle must add up to 180°, it follows that the inscribed angle equals θ, half of the central angle.
This result may be extended to an arbitrarily inscribed angle by drawing a diameter from the vertex of the angle. This converts the general problem into two sub-cases in which a diameter is a leg of each angle. The arbitrary angle equals half of the sum of the two central angles that share the diameter as a leg. Adding the two subangles again yields the result that the inscribed angle is half of the central angle.
Note that the central angle for the golden inscribed angle is 360° − 2θ. Therefore, the half of it (and thus the measure of the golden inscribed angle) is 180° − θ.
The set of all points (locus) for which a line segment can be seen at angle measured θ contains two arcs (one of each side of the line segment with central angle 2θ). In the special case of 90°, there is exactly one circle with center the middle of the line segment.
Corollaries
By a similar argument, the angle between a chord and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles.
References
- 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534 - 20 year-old Real Estate Agent Rusty from Saint-Paul, has hobbies and interests which includes monopoly, property developers in singapore and poker. Will soon undertake a contiki trip that may include going to the Lower Valley of the Omo.
My blog: http://www.primaboinca.com/view_profile.php?userid=5889534
External links
I had like 17 domains hosted on single account, and never had any special troubles. If you are not happy with the service you will get your money back with in 45 days, that's guaranteed. But the Search Engine utility inside the Hostgator account furnished an instant score for my launched website. Fantastico is unable to install WordPress in a directory which already have any file i.e to install WordPress using Fantastico the destination directory must be empty and it should not have any previous installation files. When you share great information, others will take note. Once your hosting is purchased, you will need to setup your domain name to point to your hosting. Money Back: All accounts of Hostgator come with a 45 day money back guarantee. If you have any queries relating to where by and how to use Hostgator Discount Coupon, you can make contact with us at our site. If you are starting up a website or don't have too much website traffic coming your way, a shared plan is more than enough. Condition you want to take advantage of the worldwide web you prerequisite a HostGator web page, -1 of the most trusted and unfailing web suppliers on the world wide web today. Since, single server is shared by 700 to 800 websites, you cannot expect much speed.
Hostgator tutorials on how to install Wordpress need not be complicated, especially when you will be dealing with a web hosting service that is friendly for novice webmasters and a blogging platform that is as intuitive as riding a bike. After that you can get Hostgator to host your domain and use the wordpress to do the blogging. Once you start site flipping, trust me you will not be able to stop. I cut my webmaster teeth on Control Panel many years ago, but since had left for other hosting companies with more commercial (cough, cough) interfaces. If you don't like it, you can chalk it up to experience and go on. First, find a good starter template design. When I signed up, I did a search for current "HostGator codes" on the web, which enabled me to receive a one-word entry for a discount. Your posts, comments, and pictures will all be imported into your new WordPress blog.- Relationship Between Central Angle and Inscribed Angle
- Munching on Inscribed Angles at cut-the-knot
- Arc Central Angle With interactive animation
- Arc Peripheral (inscribed) Angle With interactive animation
- Arc Central Angle Theorem With interactive animation





















