Gabriel's Horn: Difference between revisions
en>Donner60 Reverted 1 edit by 131.104.253.31 (talk) to last revision by 75.148.94.222. (TW) |
|||
| Line 1: | Line 1: | ||
{{Redirect-acronym|Nested set|the [[Nested set model]] in relational databases}} | |||
[[File:Nested_set_V4.svg|thumb|400px|<math>~V_4~</math> represented with circles in place of [[Bracket_(mathematics)#Sets_and_groups|curly brackets]] [[File:Loupe light.svg|15px|link=http://upload.wikimedia.org/wikipedia/commons/thumb/1/1b/Nested_set_V4.svg/1600px-Nested_set_V4.svg.png]] ]] | |||
In [[mathematics]] and [[set theory]], '''hereditarily finite sets''' are defined [[recursion|recursively]] as [[finite set]]s consisting of 0 or more hereditarily finite sets. | |||
==Formal definition== | |||
A recursive definition of a hereditarily finite set goes as follows: | |||
: ''Base case'': The empty set is a hereditarily finite set. | |||
: ''Recursion rule'': If ''a''<sub>1</sub>,...,''a''<sub>''k''</sub> are hereditarily finite, then so is {''a''<sub>1</sub>,...,''a''<sub>''k''</sub>}. | |||
The set of all hereditarily finite sets is denoted ''V''<sub>ω</sub>. If we denote ''P''(''S'') for the [[power set]] of ''S'', ''V''<sub>ω</sub> can also be constructed by first taking the empty set written ''V''<sub>0</sub>, then ''V''<sub>1</sub> = ''P''(''V''<sub>0</sub>), ''V''<sub>2</sub> = ''P''(''V''<sub>1</sub>),..., ''V''<sub>''k''</sub> = ''P''(''V''<sub>''k''−1</sub>),... Then | |||
:<math>\bigcup_{k=0}^\infty V_k = V_\omega.</math> | |||
==Discussion== | |||
The hereditarily finite sets are a subclass of the [[Von Neumann universe]]. They are a [[model theory|model]] of the axioms consisting of the [[Zermelo–Fraenkel axioms|axioms of set theory]] with the [[axiom of infinity]] replaced by its negation, thus proving that the axiom of infinity is not a consequence of the other axioms of set theory. | |||
Notice that there are [[countably]] many hereditarily finite sets, since ''V<sub>n</sub>'' is finite for any finite ''n'' (its [[cardinality]] is <sup>''n''−1</sup>2, see [[tetration]]), and the union of countably many finite sets is countable. | |||
Equivalently, a set is hereditarily finite if and only if its [[transitive set|transitive closure]] is finite. V<sub>ω</sub> is also symbolized by <math>H_{\aleph_0}</math>, meaning hereditarily of cardinality less than <math>\aleph_0</math>. | |||
==See also== | |||
*[[Hereditarily countable set]] | |||
{{Set theory}} | |||
[[Category:Set theory]] | |||
Revision as of 22:51, 1 February 2014
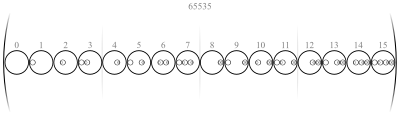

In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.
Formal definition
A recursive definition of a hereditarily finite set goes as follows:
- Base case: The empty set is a hereditarily finite set.
- Recursion rule: If a1,...,ak are hereditarily finite, then so is {a1,...,ak}.
The set of all hereditarily finite sets is denoted Vω. If we denote P(S) for the power set of S, Vω can also be constructed by first taking the empty set written V0, then V1 = P(V0), V2 = P(V1),..., Vk = P(Vk−1),... Then
Discussion
The hereditarily finite sets are a subclass of the Von Neumann universe. They are a model of the axioms consisting of the axioms of set theory with the axiom of infinity replaced by its negation, thus proving that the axiom of infinity is not a consequence of the other axioms of set theory.
Notice that there are countably many hereditarily finite sets, since Vn is finite for any finite n (its cardinality is n−12, see tetration), and the union of countably many finite sets is countable.
Equivalently, a set is hereditarily finite if and only if its transitive closure is finite. Vω is also symbolized by , meaning hereditarily of cardinality less than .



