Clebsch surface: Difference between revisions
en>Dthomsen8 Added {{no footnotes}} tag to article (TW) |
en>Mark viking Added wl |
||
| Line 1: | Line 1: | ||
[[Image:An_image_describing_the_semi-major_and_semi-minor_axis_of_eclipse.png|thumb|upright=2.5|The semi-major and semi-minor axis of an ellipse]] | |||
In [[geometry]], the '''major axis''' of an [[ellipse]] is the longest diameter: a line (line segment) that runs through the center and both [[focus (geometry)|foci]], with ends at the widest points of the shape. The '''semi-major axis''' is one half of the major axis, and thus runs from the centre, through a [[focus (geometry)|focus]], and to the edge of the ellipse; essentially, it is the radius of an orbit at the orbit's two most distant points. For the special case of a circle, the semi-major axis is the radius. One can think of the semi-major axis as an ellipse's ''long radius''. | |||
The length of the semi-major axis ''a'' of an ellipse is related to the [[Semi-minor axis|semi-minor axis']] length ''b'' through the [[eccentricity (mathematics)|eccentricity]] ''e'' and the [[semi-latus rectum]] ''ℓ'', as follows: | |||
:<math>b = a \sqrt{1-e^2},\,</math> | |||
:<math>\ell=a(1-e^2),\,</math> | |||
:<math>a\ell=b^2.\,</math> | |||
The '''semi-major axis of a [[hyperbola]]''' is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to either vertex (turning point) of the hyperbola. | |||
A [[parabola]] can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ''ℓ'' fixed. Thus <math>a\,\!</math> and <math>b\,\!</math> tend to infinity, ''a'' faster than ''b''. | |||
==Ellipse== | |||
The semi-major axis is the mean value of the smallest and largest distances from one focus to the points on the ellipse. Now consider the equation in [[coordinates (elementary mathematics)|polar coordinates]], with one focus at the origin and the other on the negative ''x''-axis, | |||
: <math>r(1+e\cos\theta)=\ell.\,</math> | |||
The mean value of <math>r={\ell\over{1-e}}\,\!</math> and <math>r={\ell\over{1+e}}\,\!</math>, (for <math>\theta = \pi \, \text{and} \, \theta = 0</math>) is | |||
: <math>a={\ell\over 1-e^2}.\,</math> | |||
In an ellipse, the semimajor axis is the [[geometric mean]] of the distance from the center to either focus and the distance from the center to either directrix. | |||
==Hyperbola== | |||
The '''semi-major axis of a [[hyperbola]]''' is, depending on the convention, plus or minus one half of the distance between the two branches; if this is ''a'' in the ''x''-direction the equation is: | |||
: <math>\frac{\left( x-h \right)^2}{a^2} - \frac{\left( y-k \right)^2}{b^2} = 1.</math> | |||
In terms of the semi-latus rectum and the eccentricity we have | |||
: <math>a={\ell \over e^2-1 }. </math> | |||
The '''transverse axis''' of a hyperbola coincides with the semi-major axis.<ref>[http://www.geom.uiuc.edu/docs/reference/CRC-formulas/node27.html 7.1 Alternative Characterization<!-- Bot generated title -->]</ref> | |||
==Astronomy== | |||
===Orbital period=== | |||
In [[astrodynamics]] the [[orbital period]] ''T'' of a small body orbiting a central body in a circular or elliptical orbit is: | |||
: <math>T = 2\pi\sqrt{a^3 \over \mu}</math> | |||
where: | |||
: ''a'' is the length of the orbit's semi-major axis | |||
: <math> \mu</math> is the [[standard gravitational parameter]] of the central body | |||
Note that for all ellipses with a given semi-major axis, the orbital period is the same, regardless of eccentricity. | |||
The [[specific angular momentum]] ''H'' of a small body orbiting a central body in a circular or elliptical orbit is: | |||
:<math>H = \sqrt{a \cdot \mu \cdot (1-e^2)} </math> | |||
where: | |||
: ''a'' and <math>\mu</math> are as defined above | |||
: ''e'' is the eccentricity of the orbit | |||
In [[astronomy]], the semi-major axis is one of the most important [[orbital elements]] of an [[orbit]], along with its [[orbital period]]. For [[Solar System]] objects, the semi-major axis is related to the period of the orbit by [[Kepler's laws of planetary motion|Kepler's third law]] (originally [[empirical]]ly derived), | |||
: <math>T^2 \propto a^3 \,</math> | |||
where ''T'' is the period and ''a'' is the semimajor axis. This form turns out to be a simplification of the general form for the [[two-body problem]], as determined by [[Isaac Newton|Newton]]: | |||
: <math>T^2= \frac{4\pi^2}{G(M+m)}a^3\,</math> | |||
where ''G'' is the [[gravitational constant]], ''M'' is the [[mass]] of the central body, and ''m'' is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that ''m'' may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered. | |||
The orbiting body's path around the [[center of mass|barycentre]] and its path relative to its primary are both ellipses. The semi-major axis is sometimes used in astronomy as the primary-to-secondary distance when the mass ratio of the primary to the secondary is significantly large (M»m); thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth–Moon system. The mass ratio in this case is 81.30059. The Earth–Moon characteristic distance, the semi-major axis of the ''geocentric'' lunar orbit, is 384,400 km. The ''barycentric'' lunar orbit, on the other hand, has a semi-major axis of 379,700 km, the Earth's counter-orbit taking up the difference, 4,700 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives a geocentric lunar average orbital speed of 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value. | |||
===Average distance=== | |||
It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite accurate, as it depends on what the average is taken over. | |||
*averaging the distance over the [[eccentric anomaly]] (q.v.) indeed results in the semi-major axis. | |||
*averaging over the [[true anomaly]] (the true orbital angle, measured at the focus) results, oddly enough, in the [[semi-minor axis]] <math>b = a \sqrt{1-e^2}\,\!</math>. | |||
*averaging over the [[mean anomaly]] (the fraction of the orbital period that has elapsed since pericentre, expressed as an angle), finally, gives the time-average | |||
:: <math>a \left(1 + \frac{e^2}{2}\right).\,</math> | |||
The time-averaged value of the reciprocal of the radius, ''r''<sup> −1</sup>, is ''a''<sup> −1</sup>. | |||
<!-- Commenter's note: This is not an equation, and seems to have no point. What did the contributor try to say? | |||
For [[exoplanet]]s orbiting the stars of different masses, using just the Kepler's third law is impractical. Here is the equation below: | |||
: <math>\sqrt[3]{M_{star}} \times \sqrt[3]{t^2}</math> | |||
where: | |||
:<math>M_{star}</math> is the mass of the star in [[solar mass]]es | |||
:<math>t</math> is the orbital period in years. | |||
--> | |||
===Energy; calculation of semi-major axis from state vectors=== | |||
In [[astrodynamics]] '''semi-major axis''' ''a'' can be calculated from [[orbital state vectors]]: | |||
: <math> a = -{\mu \over {2\varepsilon}}\,</math> | |||
for an [[elliptical orbit]] and, depending on the convention, the same or | |||
: <math> a = {\mu \over {2\varepsilon}}\,</math> | |||
for a [[hyperbolic trajectory]] | |||
and | |||
: <math> \varepsilon = { v^2 \over {2} } - {\mu \over \left | \mathbf{r} \right |} </math> | |||
([[specific orbital energy]]) | |||
and | |||
: <math> \mu = G(M+m ) \,</math> | |||
([[standard gravitational parameter]]), where: | |||
* ''v'' is orbital velocity from [[Orbital state vectors#Velocity vector|velocity vector]] of an orbiting object, | |||
* <math> \mathbf{r }\,</math> is [[cartesian coordinate system|cartesian]] [[Orbital state vectors#Position vector|position vector]] of an orbiting object in coordinates of a [[Frame of reference|reference frame]] with respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun), | |||
* ''G'' is the [[gravitational constant]], | |||
* ''M'' and ''m'' are the masses of the bodies. | |||
* <math> \varepsilon </math>, is the Energy of the orbiting body. | |||
Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the total specific energy is always the same. This statement will always be true under any given conditions. | |||
== References == | |||
{{reflist}} | |||
== External links == | |||
*[http://www.mathopenref.com/ellipsesemiaxes.html Semi-major and semi-minor axes of an ellipse] With interactive animation | |||
{{orbits}} | |||
[[Category:Conic sections]] | |||
[[Category:Orbits]] | |||
<!-- [[Category:Astronomy]] too general --> | |||
Revision as of 05:12, 4 October 2013
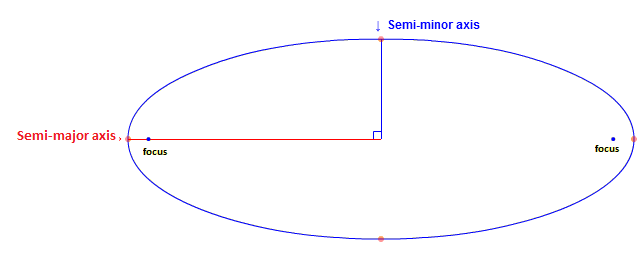
In geometry, the major axis of an ellipse is the longest diameter: a line (line segment) that runs through the center and both foci, with ends at the widest points of the shape. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus, and to the edge of the ellipse; essentially, it is the radius of an orbit at the orbit's two most distant points. For the special case of a circle, the semi-major axis is the radius. One can think of the semi-major axis as an ellipse's long radius.
The length of the semi-major axis a of an ellipse is related to the semi-minor axis' length b through the eccentricity e and the semi-latus rectum ℓ, as follows:
The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to either vertex (turning point) of the hyperbola.
A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ℓ fixed. Thus and tend to infinity, a faster than b.
Ellipse
The semi-major axis is the mean value of the smallest and largest distances from one focus to the points on the ellipse. Now consider the equation in polar coordinates, with one focus at the origin and the other on the negative x-axis,
The mean value of and , (for ) is
In an ellipse, the semimajor axis is the geometric mean of the distance from the center to either focus and the distance from the center to either directrix.
Hyperbola
The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches; if this is a in the x-direction the equation is:
In terms of the semi-latus rectum and the eccentricity we have
The transverse axis of a hyperbola coincides with the semi-major axis.[1]
Astronomy
Orbital period
In astrodynamics the orbital period T of a small body orbiting a central body in a circular or elliptical orbit is:
where:
- a is the length of the orbit's semi-major axis
- is the standard gravitational parameter of the central body
Note that for all ellipses with a given semi-major axis, the orbital period is the same, regardless of eccentricity.
The specific angular momentum H of a small body orbiting a central body in a circular or elliptical orbit is:
where:
In astronomy, the semi-major axis is one of the most important orbital elements of an orbit, along with its orbital period. For Solar System objects, the semi-major axis is related to the period of the orbit by Kepler's third law (originally empirically derived),
where T is the period and a is the semimajor axis. This form turns out to be a simplification of the general form for the two-body problem, as determined by Newton:
where G is the gravitational constant, M is the mass of the central body, and m is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that m may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered.
The orbiting body's path around the barycentre and its path relative to its primary are both ellipses. The semi-major axis is sometimes used in astronomy as the primary-to-secondary distance when the mass ratio of the primary to the secondary is significantly large (M»m); thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth–Moon system. The mass ratio in this case is 81.30059. The Earth–Moon characteristic distance, the semi-major axis of the geocentric lunar orbit, is 384,400 km. The barycentric lunar orbit, on the other hand, has a semi-major axis of 379,700 km, the Earth's counter-orbit taking up the difference, 4,700 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives a geocentric lunar average orbital speed of 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value.
Average distance
It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite accurate, as it depends on what the average is taken over.
- averaging the distance over the eccentric anomaly (q.v.) indeed results in the semi-major axis.
- averaging over the true anomaly (the true orbital angle, measured at the focus) results, oddly enough, in the semi-minor axis .
- averaging over the mean anomaly (the fraction of the orbital period that has elapsed since pericentre, expressed as an angle), finally, gives the time-average
The time-averaged value of the reciprocal of the radius, r −1, is a −1.
Energy; calculation of semi-major axis from state vectors
In astrodynamics semi-major axis a can be calculated from orbital state vectors:
for an elliptical orbit and, depending on the convention, the same or
for a hyperbolic trajectory
and
and
(standard gravitational parameter), where:
- v is orbital velocity from velocity vector of an orbiting object,
- is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun),
- G is the gravitational constant,
- M and m are the masses of the bodies.
- , is the Energy of the orbiting body.
Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the total specific energy is always the same. This statement will always be true under any given conditions.
References
43 year old Petroleum Engineer Harry from Deep River, usually spends time with hobbies and interests like renting movies, property developers in singapore new condominium and vehicle racing. Constantly enjoys going to destinations like Camino Real de Tierra Adentro.
External links
- Semi-major and semi-minor axes of an ellipse With interactive animation
The name of the writer is Garland. Playing croquet is something I will never give up. He presently life in Idaho and his mothers and fathers reside close by. Bookkeeping is what he does.
my web-site: extended auto warranty
























